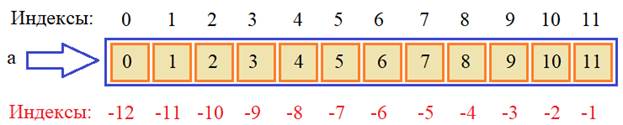
Индексация, срезы, итерирование массивов

Смотреть материал на видео

На этом занятии познакомимся со способами считывания и записи значений в массивы NumPy. В целом синтаксис очень похож на обращение к элементам списков языка Python. Давайте рассмотрим все на конкретных примерах. Предположим, что имеется одномерный массив:

a = np.arange(12) # array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

И мы хотим прочитать отдельные его элементы. Это можно сделать путем обращения к нужному элементу массива по его индексу, например, так:

a[2] # увидим значение 2

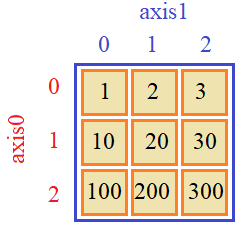
Помимо положительных индексов существуют еще и отрицательные, которые отсчитывают элементы с конца списка, например:

a[-1] # последнее значение 11
a[-2] # предпоследнее значение 10

Если мы выходит за пределы массива и указываем несуществующий индекс, то возникает исключение (ошибка):

a[12] # ошибка, последний индекс 11

Соответственно, если нужно изменить значение какого-либо элемента, то ему просто присваивается это новое значение:

a[0] = 100 # первый элемент равен 100

Как видите, здесь применяется тот же синтаксис, что и при работе с обычными списками Python. То же касается и срезов. Мы можем выделять и менять сразу группу элементов массива. Общий синтаксис срезов выглядит так:

<имя массива>[start:stop:step]

Давайте посмотрим примеры использования этой конструкции:

b = a[2:4] # array([2, 3])

Здесь указан начальный индекс 2, конечный индекс 4 и по умолчанию берется шаг, равный 1. На выходе получаем массив из двух значений 2 и 3. Последний граничный индекс 4 не включается в срез.

Обратите внимание, в NumPy срезы возвращают новое представление того же самого массива, то есть, данные, на которые ссылаются переменные a и b одни и те же. Мы в этом можем легко убедиться, выполнив вот такую строчку:

b[0] = -100

и это приводит к изменению соответствующего элемента массива a:

array([ 100, 1, -100, 3, 4, 5, 6, 7, 8, 9, 10, 11])

Поэтому срезы – это не копии массивов, а лишь создание их нового представления. Это сделано специально для экономии памяти.

Другие примеры срезов:

a[3:] # array([ 3,  4,  5,  6,  7,  8,  9, 10, 11])
a[:5] # array([ 100,    1, -100,   3,    4])
a[-5: -1] # array([ 7,  8,  9, 10])
a[:] # array([ 100,    1, -100,    3,   4,    5,    6,    7,    8,    9,   10,   11])
a[1:6:2] # array([1, 3, 5])
a[::2] # array([ 100, -100,    4,   6,    8,   10])
a[::-1]# array([  11,   10,    9,    8,    7,    6,    5,    4,    3, -100,  1,  100])

Я, думаю, общий принцип использования одномерных срезов понятен. Разумеется, срезам можно присваивать новые значения. Например, так:

a[:4] = [-1, -2, -3, -4] # присваивание списка Python
a[4::2] = np.array([10, 20, 30, 40]) # присваивание массива NumPy

Элементы массива NumPy можно перебирать с помощью цикла for, так как массивы – итерируемые объекты. Например:

for x in a:
     print(x, sep=' ', end=' ')

Индексация и срезы многомерных массивов

В базовом варианте индексация и срезы многомерных массивов работают также как и в одномерных, только индексы указываются для каждой оси. Например, объявим двумерный массив:

x = np.array([(1, 2, 3), (10, 20, 30), (100, 200, 300)])

Для обращения к центральному значению 20 нужно выбрать вторую строку и второй столбец, имеем:

x[1, 1] # значение 20

Чтобы взять последнюю строку и последний столбец, можно использовать отрицательные индексы:

x[-1, -1] # значение 300

Если же указать только один индекс, то получим строку:

x[0] # array([1, 2, 3])

Эта запись эквивалентна следующей:

x[0, :] # array([1, 2, 3])

То есть, не указывая какие-либо индексы, NumPy автоматически подставляет вместо них полные срезы.

Для извлечения столбцов мы уже должны явно указать полный срез в качестве первого индекса:

x[:,1] # array([  2,  20, 200])

Итерирование двумерных массивов можно выполнять с помощью вложенных циклов, например:

for row in x:
    for val in row:
        print(val, end=' ')
    print()

Если же необходимо просто перебрать все элементы многомерного массива, то можно использовать свойство flat:

for val in x.flat:
    print(val, end=' ')

У массивов более высокой размерности картина индексации, в целом выглядит похожим образом. Например, создадим четырехмерный массив:

a = np.arange(1, 82).reshape(3, 3, 3, 3)

Тогда для обращения к конкретному элементу следует указывать четыре индекса:

a[1, 2, 0, 1] # число 47

Для выделения многомерного среза, можно использовать такую запись:

a[:, 1, :, :] # матрица 3x3x3

или, так:

a[0, 0] # двумерная матрица 3x3

Это эквивалентно записи:

a[0, 0, :, :]

Если же нужно задать два последних индекса, то полные срезы у первых двух осей указывать обязательно:

a[:, :, 1, 1] # матрица 3x3
a[0:2, 0:2, 1, 1] # матрица 2x2

Пакет NumPy позволяет множество полных подряд идущих срезов заменять троеточиями. Например, вместо a[:, :, 1, 1] можно использовать запись:

a[..., 1, 1] # эквивалент a[:, :, 1, 1]

Это бывает удобно, когда у массива много размерностей и нам нужны последние индексы.

Списочная индексация

Помимо указания у массивов обычных индексов или срезов в NumPy существует еще один способ индексирования – через списки или массивы целых чисел. Чтобы лучше понять, о чем идет речь, рассмотрим этот механизм на примерах. Для простоты возьмем одномерный массив с какими-нибудь значениями:

a = np.arange(1, 9) # array([1, 2, 3, 4, 5, 6, 7, 8])

Далее, смотрите, если указать обычный числовой индекс, то получим одно значение соответствующего элемента:

a[0] # значение 1

Но, если вместо числового индекса указать список:

b = a[[0]] # array([1])

то на выходе уже получим копию массива из одного первого значения исходного. То есть, выполняя далее операцию:

b[0] = 100

Изменение массива b не приведет к изменению данных в массиве a.

А что будет, если в списке указать несколько индексов? Например, так:

a[[0, 1, 7, 5]] # array([1, 2, 8, 6])

На выходе получаем новый массив, состоящий из соответствующих значений. Или, можно сделать даже так:

a[[0, 0, 1, 1, 1, 2, 3, 4, 5, 6, 7]] # array([1, 1, 2, 2, 2, 3, 4, 5, 6, 7, 8])

То есть, мы здесь имеем, фактически, способ формирования новых массивов на основе других массивов. В списке достаточно перечислить индексы нужных элементов и на выходе формируется массив с соответствующими значениями. В ряде случаев такая операция бывает очень удобной.

Но здесь есть один важный нюанс. Копия массива через списочное индексирование создается, когда выражение записано справа от бинарного оператора (является выражением типа rvalue). Если же такую же конструкцию записать слева от оператора (как выражение lvalue), например, присваивания:

a[[0, 1, 2]] = [10, 20, 30]

то копия не создается, а просто в элементы этого же массива с индексами 0, 1 и 2 заносятся значения 10, 20 и 30. Далее в этом же занятии мы подробнее увидим различные варианты и особенности при присваивании значений через списочное индексирование.

Кроме обычных списков языка Python мы можем передавать и массивы NumPy, состоящие из целых значений. Например, так:

indx = np.array([0, 0, 1, 1, 1, 2])
a[indx] # array([1, 1, 2, 2, 2, 3])

Или, с булевыми значениями:

bIndx = [True, True, False, False, False, True, False, False]
a[bIndx] # array([1, 2, 6])

В результате останутся только те элементы, которым соответствуют индексы True. Причем, длина списка (или массива) bIndx должна совпадать с длиной массива a, иначе произойдет ошибка.

Последний вариант списочной индексации используется очень часто. Например, мы можем сформировать массив индексов путем какой-либо булевой операции над массивом:

i = a > 5 # array([False, False, False, False, False,  True,  True,  True])

А, затем, использовать его, чтобы оставить только нужные элементы:

a[i] # array([6, 7, 8])

Или, все это можно записать короче в одну строчку:

a[a > 5] # array([6, 7, 8])

Как видите, это невероятно удобный механизм обработки данных массивов пакета NumPy.

Списочная индексация и многомерные массивы

Фактически, массив индексов определяет значения и форму создаваемого массива. Например, если взять тот же одномерный массив:

a = np.arange(1, 9)

но набор индексов определить как двумерный массив:

i = np.array([[0, 1], [2, 3]])

то на выходе будет формироваться уже двумерный массив:

a[i] # array([[1, 2], [3, 4]])

Только в этом случае индексы i должны определяться именно массивом NumPy, а не списком Python.

Так можно создавать массивы любых размерностей. Давайте теперь посмотрим, как будет себя вести списочное индексирование с многомерными массивами. Возьмем двумерный массив:

a = np.arange(1, 13).reshape(3, 4)

и одномерный список индексов:

indx = [2, 1, 0]
a[indx]

На выходе получим массив:

array([[ 9, 10, 11, 12],
[ 5, 6, 7, 8],
[ 1, 2, 3, 4]])

Смотрите, здесь индексы обозначают номера строк двумерного массива. В результате, строки нового массива идут в обратном порядке. Далее, пропишем индексы в виде двумерного массива:

indx = np.array([[1, 0], [2, 1]])
a[indx]

Результатом будет трехмерный массив:

array([[[ 5, 6, 7, 8],
        [ 1, 2, 3, 4]],

       [[ 9, 10, 11, 12],
        [ 5, 6, 7, 8]]])

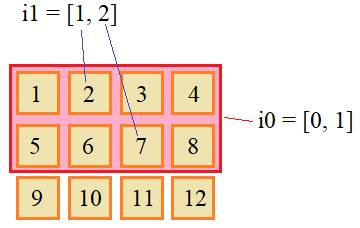
Что здесь произошло? В действительности, каждый индекс двумерного массива соответствует определенной строке этого массива. А двумерная форма индексов лишь указывает как упаковать строки в новом массиве. То есть, вместо каждого индекса подставляется своя строка и получается трехмерный массив.

Если же мы хотим выбирать из двумерного массива не строки, а отдельные элементы и на их основе формировать новые массивы, то следует использовать два списка. Первый список по прежнему будет указывать строки массива, а второй – индексы столбцов у каждой строки. Например, так:

i0 = [0, 1]
i1 = [1, 2]
a[i0, i1] # array([2, 7])

Работу такого списочного индексирования можно представить в виде:

При множественной списочной индексации допускается указывать конкретные индексы и срезы. Например:

a[:, i1]

В этом случае получим уже матрицу 3x2, то есть, второй список i1 здесь используется для выделения столбцов целиком, а не одного только элемента. Соответственно, строчка:

a[i0, 1] # array([2, 6])

выделим массив из двух значений 2 и 6.

Изменение массивов через списочную индексацию

С помощью списков можно не только создавать новые массивы, но и менять значения в исходном. Например, возьмем одномерный массив:

a = np.arange(7) # array([0, 1, 2, 3, 4, 5, 6])

и изменим его следующие элементы:

a[[0, 4, 6]] = [-1, -2, -3] # array([-1,  1,  2,  3, -2,  5, -3])

Смотрите, как это удобно. Мы сразу списком индексов обозначаем изменяемые элементы и присваиваем им соответствующие новые значения.

Если в списке индексов имеются повторы, то новое значение будет соответствовать последнему значению:

a[[0, 0, 0, 1]] = [1, 2, 3, 100] # array([  3, 100,   2,   3,  -2,   5,  -3])

Здесь в первый элемент (с индексом 0), в итоге, запишется число 3. Или можно выполнить вот такую операцию:

a[[0, 0, 0]] = a[[0, 0, 0]] + 3

Здесь сначала будет выполнена операция списочного индексирования a[[0, 0, 0]], а уже потом добавлено значение 3. То есть, это запись эквивалентна следующей:

a[0] = a[0] + 3

Аналогично все выполняется и при такой команде:

a[[0, 0, 1, 2]] += 1 # array([  7, 101,  3,   3,  -2,   5,  -3])

Она эквивалента записи:

a[[0, 1, 2]] += 1 # array([  7, 101,   3,   3,  -2,   5,  -3])

Соответственно, элементам с индексами 0, 1 и 2 будет прибавлена 1. Вот этот момент следует иметь в виду при работе с массивами NumPy.

Те же самые математические операции и операции присваивания можно выполнять и с многомерными массивами. Работает все аналогичным образом. Вот так вот работают индексы, срезы и списочное индексирование в пакете NumPy.

Индексация, срезы, итерирование массивов

Индексация и срезы многомерных массивов

Списочная индексация

Списочная индексация и многомерные массивы

Изменение массивов через списочную индексацию

Видео по теме