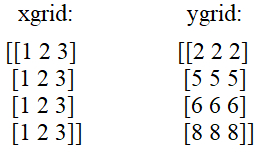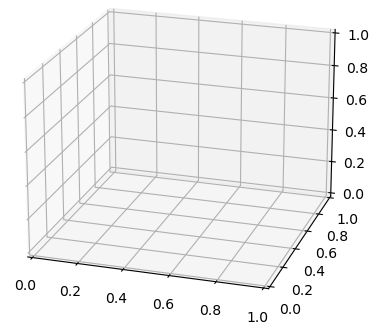
Как строить трехмерные графики

Смотреть материал на видео

Следующим шагом мы с вами рассмотрим возможности построения трехмерных графиков в пакете matplotlib. Такая возможность появилась, начиная с версии 0.99, поэтому убедитесь, что ваш пакет поддерживает трехмерные графики.

Все дополнительные классы для работы в 3D находятся в модуле:

mpl_toolkits.mplot3d

и вначале мы его импортируем в нашу программу наряду с самим пакетом matplotlib и numpy:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

А, затем, создадим трехмерную систему координат:

fig = plt.figure(figsize=(7, 4))
ax_3d = Axes3D(fig)
 
plt.show()

При выполнении этой простой программы, мы в окне увидим три пространственные оси, которые можно вращать с помощью курсора мышки:

Того же самого результат можно добиться, используя параметр projection при создании системы координат:

fig = plt.figure(figsize=(7, 4))
ax_3d = fig.add_subplot(projection='3d')

Как именно создавать трехмерные оси, зависит от вашего выбора и удобства при написании конкретных программ. Я остановлюсь на втором способе.

После создания координатных осей мы можем в них строить двумерные и трехмерные графики с помощью того же самого набора функций:

plot() – линейный 2D график в трех измерениях;
step() – ступенчатый 2D график в трех измерениях;
scatter() – точеный график 3D график.

Также нам становятся доступными следующие дополнительные функции:

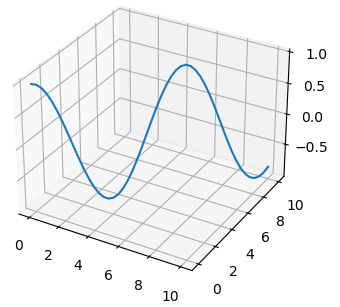
plot_wireframe() – построение каркасной поверхности в 3D;
plot_surface() – построение непрерывной 3D поверхности.

Начнем с самого простого варианта – функции plot() для рисования косинусоиды в трех измерениях:

x = np.linspace(0, 10, 50)
z = np.cos(x)
ax_3d.plot(x, x, z)

То есть, мы здесь по координатам x, y выбираем одни и те же значения, а координата z (вертикаль) – это значение функции. Давайте подпишем оси, чтобы видеть, где какая расположена на этом графике:

ax_3d.set_xlabel('x')
ax_3d.set_ylabel('y')
ax_3d.set_zlabel('z')

Но то, что мы получили, это не совсем трехмерный график. Скорее, это двумерная косинусоида в трех измерениях. Давайте построим настоящее трехмерное изображение, например, вот такой функции:

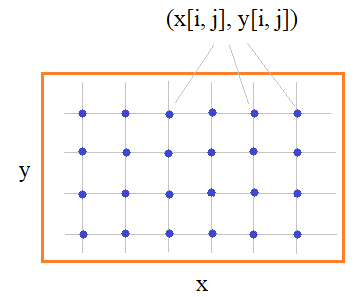
Первое, что нам здесь нужно сделать – это сформировать двумерную сетку координат по осям x и y:

То есть, должны быть сформированы двумерные массивы x, y, которые для текущей точки с индексами (i, j) возвращают ее координаты в плоскости xy.

Для регулярных сеток эти массивы можно сформировать следующим образом. Определим множество координат x (для столбцов) и y (для строк), например, так:

x = [1, 2, 3]
y = [2, 5, 6, 8]

А, затем, используя функцию meshgrid() сформируем регулярную сетку на основе этих данных:

xgrid, ygrid = np.meshgrid(x, y)

На выходе получим двумерные массивы со значениями:

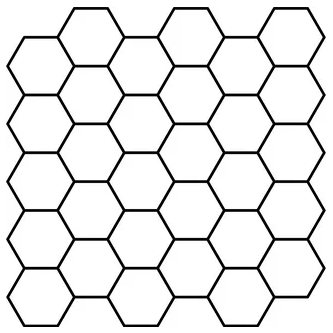
То есть, смотрите, теперь для любой пары индексов (i, j) мы легко сможем получить координаты точки в плоскости xy:

(xgrid[1, 2], ygrid[1, 2]) = (3, 5)
(xgrid[3, 0], ygrid[3, 0]) = (1, 8)

Но зачем было так все усложнять? Почему бы не использовать одномерные массивы x, y вместо двумерных xgrid, ygrid? Дело в том, что одномерные массивы, которые описывают расположение строк и столбов, могут формировать только регулярные сетки, то есть, прямоугольные. А что, если нужно сформировать гексагональную сетку, которая выглядит, следующим образом:

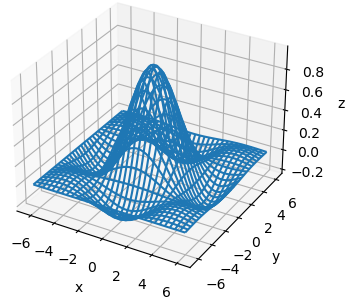
Здесь уже не получится обойтись указанными одномерными массивами, а нужно прописывать узлы двумерными массивами. Именно поэтому, в общем случае, и реализовано отображение через двумерные массивы трехмерных графиков.

Итак, давайте теперь построим полноценный трехмерный график синусоиды на регулярной сетке. Для этого мы сначала сформируем координаты узлов в плоскости xy:

x = np.arange(-2*np.pi, 2*np.pi, 0.2)
y = np.arange(-2*np.pi, 2*np.pi, 0.2)
xgrid, ygrid = np.meshgrid(x, y)

А, затем, вычислим значения синусоиды в этих узлах:

zgrid = np.sin(xgrid) * np.sin(ygrid) / (xgrid * ygrid)

Если для вывода такого графика воспользоваться функцией plot_wireframe():

ax_3d.plot_wireframe(xgrid, ygrid, zgrid)

то результат будет следующий:

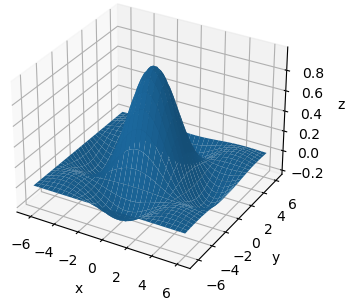
Как видите, мы получили полноценный каркасный трехмерный график синусоиды. Или же можно построить полноценную поверхность в виде синусоиды, используя функцию plot_surface():

ax_3d.plot_surface(xgrid, ygrid, zgrid)

Фактически, только этим две эти функции и отличаются друг от друга: первая строит 3D-каркас, а вторая 3D-поверхность.

У этих функций есть следующие параметры для настройки внешнего вида графика:

Параметр	Описание
x, y, z	2D массивы для построения трехмерных графиков.
rcount, ccount	Максимальное число элементов каркаса по координатам x и y (по умолчанию 50).
rstride, cstride	Величина шага, с которым будут выбираться элементы из массивов x, y (параметры rstride, cstride и rcount, ccount – взаимоисключающие).
color	Цвет графика
cmap	Цветовая карта графика

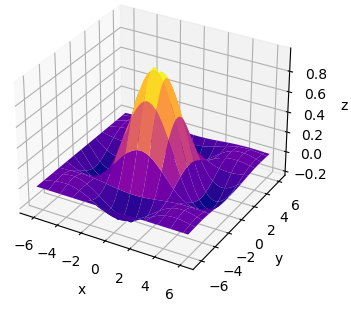
Например, если установить параметры:

ax_3d.plot_surface(xgrid, ygrid, zgrid, rstride=5, cstride=5, cmap='plasma')

то получим следующий вид нашей синусоиды:

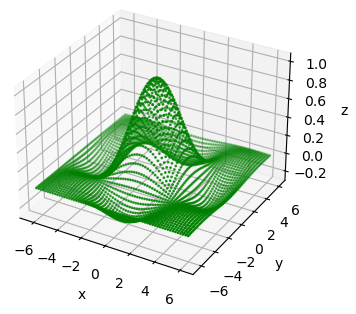
В заключение этого занятия приведу пример построения этого же графика набором точек, используя функцию scatter():

ax_3d.scatter(xgrid, ygrid, zgrid, s=1, color='g')

Увидим следующий результат:

Вот так в базовом варианте можно выполнять построения трехмерных графиков в пакете matplotlib. Этой информации достаточно для большинства прикладных задач. Ну а если потребуется реализовать что-то особенное, тогда прямой путь к документации:

https://matplotlib.org/stable/api/_as_gen/mpl_toolkits.mplot3d.axes3d.Axes3D.html

Как строить трехмерные графики

Видео по теме