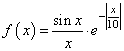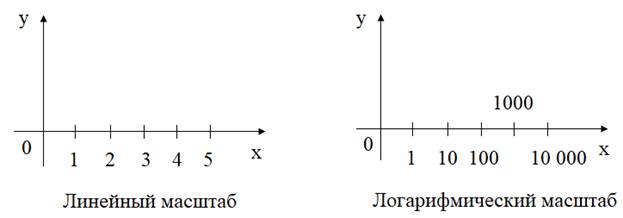
Делаем логарифмический масштаб у координатных осей

Смотреть материал на YouTube | RuTube

До сих пор мы с вами отображали графики в декартовой системе с линейным шагом изменения значений. Это довольно частый вариант, который используется в большинстве случаев. Но бывают функции, которые требуют логарифмического масштаба (изменения шага) по координатам.

Например, если сформировать график функции:

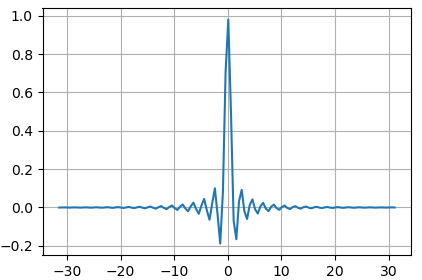
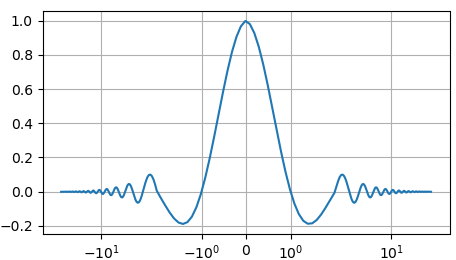
Если отобразить его в линейной системе координат:

import numpy as np
import matplotlib.pyplot as plt
 
fig = plt.figure(figsize=(7, 4))
ax = fig.add_subplot()
 
x = np.arange(-10*np.pi, 10*np.pi, 0.5)
ax.plot(x, np.sinc(x) * np.exp( -np.abs(x/10)) )
ax.grid()
 
plt.show()

То мелкие колебания функции на больших частотах будут не видны:

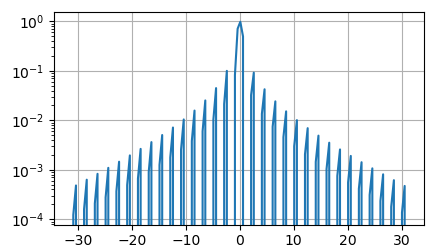
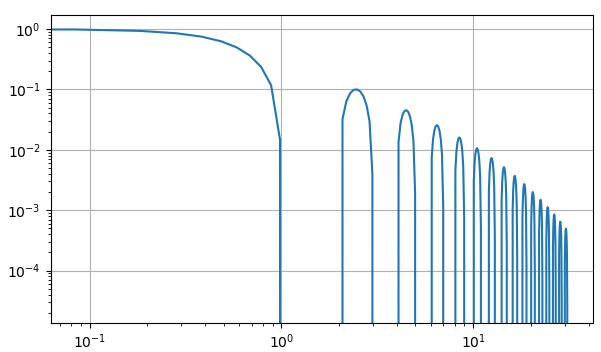
Как раз здесь может помочь логарифмический масштаб по оси ординат. Для этого достаточно воспользоваться методом semilogy(), чтобы по оси Oy откладывался логарифмический масштаб (логарифм по основанию 10) для графика:

ax.semilogy(x, np.sinc(x) * np.exp( -np.abs(x/10)) )

В результате получим следующее построение:

Видите, стало гораздо информативнее и конечному пользователю показывается больше информации о сигнале.

Аналогично, можно формировать логарифмический масштаб по оси ординат с помощью метода:

semilogx()

Того же самого эффекта можно добиться и с помощью прежней функции plot(), только дополнительно указать логарифмический масштаб по нужной оси. Например, так:

ax.plot(x, np.sinc(x) * np.exp( -np.abs(x/10)) )
ax.set_yscale('log')

Здесь был использован метод set_yscale() для изменения масштаба со значения ‘linear’ на значение ‘log’. По аналогии, можно изменить масштаб и для оси Ox с помощью метода set_xscale():

ax.set_xscale('log')

Вообще, здесь можно использовать три разных масштаба:

'linear' – линейный масштаб (используется по умолчанию);
'log' – логарифмический масштаб;
'symlog' – вблизи нуля (в указанных пределах) масштаб линейный, а в остальной области – логарифмический.

Как я только что отмечал, логарифмический масштаб формируется по основанию 10. Если нужно изменить и указать другое основание, то это делается с помощью параметра base:

ax.set_yscale('log', base=5)

Вернемся к нашему графику. Если на него внимательно посмотреть, то по вертикали дополнительно отложены небольшие риски. Это восемь промежуточных линейных значений. Например, между значениями

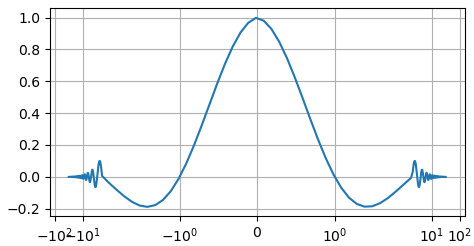
Откладываются риски со значениями:

0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2

Мы можем управлять их отображением, указав их значения в виде целых чисел в списке параметра subs:

ax.set_yscale('log', subs=[2, 9])

Здесь мы указываем отображать риску со значением 0,2 или 0,02 или 0,002 и т.д. И риску со значениями 0,9 или 0,09 или 0,009 и т.д.

Рассмотрим далее возможность использования третьего параметра 'symlog'. Мы его пропишем для оси Ox в следующем виде:

x = np.arange(-10*np.pi, 10*np.pi, 0.1)
ax.plot(x, np.sinc(x) * np.exp( -np.abs(x/10)) )
ax.set_xscale('symlog', linthresh=2)

Здесь использован дополнительный параметр linthresh, определяющий граничное значение [-2; 2], где график следует отображать в линейном масштабе. А все, что выходит за эти пределы – в логарифмическом. В результате, получим такое построение:

Дополнительно линейный масштаб можно растянуть, указав масштаб в дополнительном параметре linscale:

ax.set_xscale('symlog', linthresh=2, linscale=5)

Наконец, если нам нужно установить логарифмический масштаб по обеим осям, то проще всего для этого воспользоваться функцией loglog(), вместо функции plot() или semilogx()/semilogy():

ax.loglog(x, np.sinc(x) * np.exp( -np.abs(x/10)) )

Вот так, достаточно просто можно задавать и управлять логарифмическим масштабом при отображении графиков в пакете matplotlib.

Делаем логарифмический масштаб у координатных осей

Видео по теме