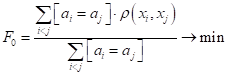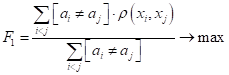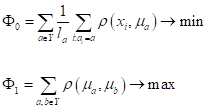Метрические методы
Метрические методы классификации. Метод k ближайших соседей
Методы парзеновского окна и потенциальных функций
Метрические регрессионные методы. Формула Надарая-Ватсона
Задачи кластеризации. Постановка задачи
Алгоритм кластеризации Ллойда (K-средних, K-means)
Алгоритм кластеризации DBSCAN
Агломеративная иерархическая кластеризация. Дендрограмма
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
Метрические методы

Задачи кластеризации. Постановка задачи

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

На предыдущих занятиях мы познакомились с несколькими распространенными метрическими подходами к задачам классификации и регрессии. В них нам была дана обучающая выборка (размеченные данные), по которым строилась модель. Но на практике встречаются задачи, когда исходный набор объектов не размечен и нужно построить модель, которая бы разносила образы по группам (классам), используя заданную (или выбранную) метрику между объектами:

Это постановка задачи кластеризации. Здесь на выходе, в общем случае, нужно найти:

множество кластеров ;
алгоритм кластеризации .

И, так как алгоритм должен сам разнести образы по классам, то задачу кластеризации относят к задачам обучения без учителя (unsupervised learning). То есть, это частная задача обучения без учителя. Помимо кластеризации существуют и совершенно другие методы, которые также относятся к обучению без учителя. Поэтому не нужно полагать, что кластеризация охватывает весь класс таких задач.

Цели кластеризации

Для чего вообще может понадобиться делать кластеризацию данных? Здесь можно выделить несколько направлений:

сложные данные разбиваются по похожим группам, упрощая их представление, а значит, и обработку в пределах каждой группы (обычно используется в задачах классификации, регрессии);
сокращение объема выборки за счет сохранения небольшого числа характерных представителей каждого класса;
выделение нетипичных объектов (выбросов), которые нельзя отнести ни к одному кластеру (задачи классификации, антифрод и спам системы);
построение иерархии объектов (пример – классификация животных и растений К. Линнея – задача таксономии).

Типы кластерных структур

Какие на этом пути возникают проблемы? Первое. Часто задачи кластеризации не имеют четко выраженного единственного решения (даже с позиции человеческого восприятия). Следующий пример показывает, как по разному можно разделить множество точек по группам:

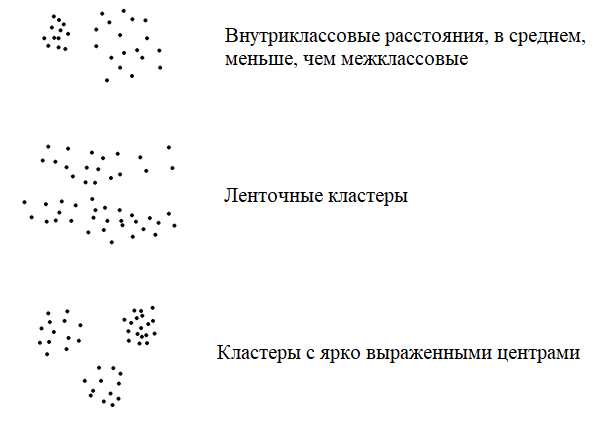
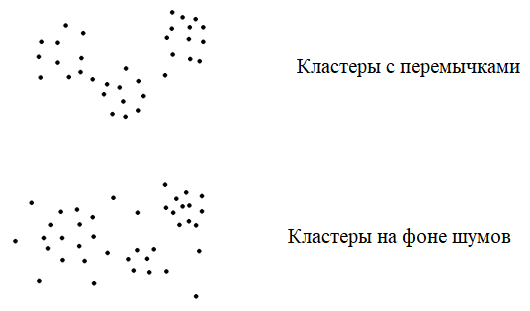
Здесь результат кластеризации может зависеть и от выбора метрики и от применяемого алгоритма и от начальных исходных данных, которые зачастую определяются случайным образом. Поэтому, для одних и тех же данных могут получаться совершенно разные результаты кластеризации.

Второе. Сами кластеры также могут образовывать разные типы структур. Вот, наиболее характерные из них:

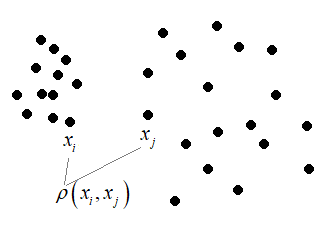
Обратите внимание, в последних двух примерах нет кластеров, как таковых. Геометрические фигуры, как правило, это не тот набор данных, который интересует заказчика (несмотря на то, что наш мозг хорошо их различает). А ниже вообще представлен один кластер. При таком распределении объектов выборки задачу кластеризации ставить бессмысленно. Тем не менее, на практике нередко бывает, что заказчик ставит задачу кластеризации для данных, которые по всем осям образуют такое единое распределение в виде одного кластера и выделить какие-либо отдельные структуры практически невозможно. В этом случае задачу следует скорректировать и решать другими методами.

Критерии качества кластеризации

Теперь, когда мы в целом представляем задачу кластеризации, нужно сформулировать критерии для оценки качества разбиения образов по группам.

Если мы можем измерять только расстояния между парами любых образов:

и имеем модель, которая выдает номер кластера:

то в качестве критериев можно выделить среднее внутрикластерное расстояние:

(оно должно стремиться к минимуму) и среднее межкластерное расстояние:

(очевидно, оно должно быть как можно больше). Объединить эти две характеристики можно, например, взяв их отношение:

Если же объекты описываются координатами в признаковом пространстве:

то можно дополнительно ввести понятие центра кластера:

и вычислять относительно них:

Объединить эти две характеристики можно также путем их отношения:

У вас здесь может возникнуть вопрос, а что это за объекты, для которых можно вычислить только расстояния между ними, но не центры кластеров? Что значит они не представлены в признаковом пространстве? Например, это могут быть расстояния между словами. Само по себе слово – это объект без числовых признаков. Но, тем не менее, существуют методики, позволяющие определять, насколько одно слово близко (или далеко) от другого слова. То же самое можно проделывать и со звуками, последовательностями нуклеотидов в ДНК и РНК и т. п. Существует немало задач, где мы можем задавать расстояния (метрику), но не признаковое пространство. Или же, нам отдельные признаки ни к чему и делать дополнительную работу просто не имеет смысла. Во всех этих случаях можно воспользоваться характеристиками для оценки качества кластеризации. Если же у нас для образов явно прописаны числовые признаки, то можно перейти к более понятным (на мой взгляд) оценкам качества .

Постановка задачи частичного обучения (Semi-Supervised Learning – SSL)

В заключение этого вводного занятия сформулирую постановку задачи частичного обучения с учителем на основе кластеризации. Давайте предположим, что в обучающей выборке есть небольшая часть (k штук) размеченных объектов:

а, остальные не размеченные:

то есть, мы не знаем для них целевых значений .

Очевидно, часть размеченных данных нам может помочь в задачах кластеризации остальных неразмеченных объектов. Для этого мы строим модель:

которая формирует выходные значения

для неразмеченных данных. И здесь различают два общих подхода к решению этой задачи:

Частичное обучение: строим алгоритм такой, что для любого входного образа (не обязательно из обучающей выборки) прогнозируется класс (номер кластера).
Трансдуктивное обучение (transductive learning): строим алгоритм такой, что только для объектов формируются прогнозы кластеров.

Где используется такой подход частичного обучения? Например, при каталогизации текстов. Когда их нужно сгруппировать по похожести, то есть, соотнести с ранее размеченными текстами (для которых имеются метки категории). То же самое касается любых типов данных, вплоть до изображений, звуков, последовательностей ДНК, и т.д.

На этом мы завершим вводное занятие по кластеризации. На следующих продолжим эту тему и рассмотрим конкретные алгоритмы разделения объектов по категориям.