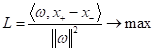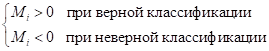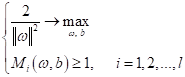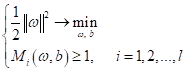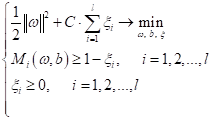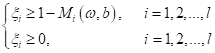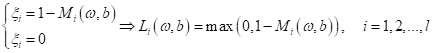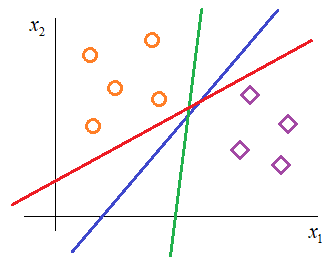
|
Введение в метод опорных векторов (SVM)Практический курс по ML: https://stepik.org/course/209247/ Давайте вновь вернемся к рассмотрению задачи бинарной классификации образов с позиции разделяющей гиперплоскости. Для простоты положим, что у нас двумерное признаковое пространство. Тогда каждый образ класса можно представить точкой на плоскости. Пусть образы обучающей выборки распределяются, следующим образом:
Как видите, для нашего примера можно построить множество различных разделяющих линий (в общем случае, гиперплоскостей) так, что каждая из них будет корректно отделять один класс от другого. И здесь возникает вопрос, какое разделение лучше? В машинном обучении мы исходим из того, что модель, обученная на некоторой выборке должна хорошо работать с другими произвольными наборами из того же распределения. То есть, модель должна иметь хорошие обобщающие способности (не быть слишком переобученной). Если с этих позиций посмотреть на проведенные разделяющие линии, то чисто интуитивно я бы выбрал синюю. Почему ее? Смотрите, красная и зеленая линии в действительности, как бы, делают дополнительные предположения о распределении образов обоих классов:
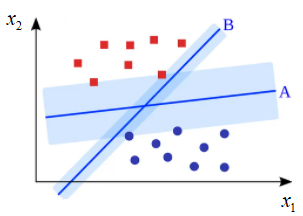
Красная «полагает», что образы распределены несколько горизонтально, а зеленая, что образы идут более вертикально. Конечно, и синяя линия «делает» свое предположение, но она чисто визуально в большей степени сохраняет исходное распределение. Вот эта идея проведения разделяющей гиперплоскости, которая бы ориентировалась только на распределение обучающей выборки и по возможности не делала бы дополнительных предположений о распределении образов в классах, положена в основу метода опорных векторов (Support Vector Machine – SVM). Давайте теперь чисто интуитивное соображение формализуем на уровне математики. И ответим на первый вопрос, что же это за разделяющая гиперплоскость, которая «делает» минимальные предположения о распределении классов и, тем самым, приводит к лучшей обобщающей способности алгоритма классификации? С точки зрения SVM, оптимальная разделяющая гиперплоскость – это та, которая образует наиболее широкую полосу между объектами двух классов. При этом сама разделяющая гиперплоскость будет точно проходить посередине этой полосы:
Почему так? Потому что, чем шире полоса, тем надежнее классификатор будет отделять образы одного класса от другого. Чтобы описать эту идею на уровне математики, мы вначале должны задать модель классификатора, которая, фактически, определяет уравнение гиперплоскости в признаковом пространстве. Мы выберем самую простую линейную модель вида:
Я ее записал здесь тремя способами, но все они означают линейную комбинацию вектора параметров ω с образом x плюс смещение -b. На выходе модель выдает значения:
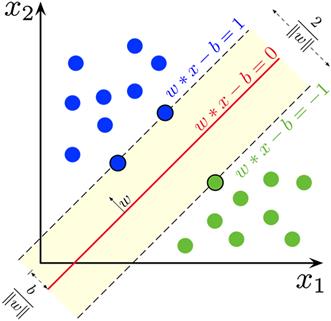
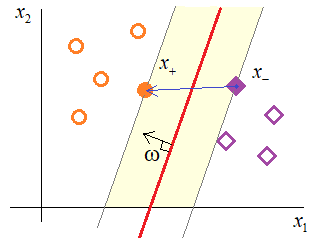
Далее, мы предположим, что наша обучающая выборка состоит из линейно разделимых образов (затем, мы этот случай обобщим на линейно неразделимый). Тогда ширина полосы будет определяться расположением граничных векторов x в признаковом пространстве:
Если взять любые
два образа разных классов, расположенные ближе всего к разделяющей границе (то
есть, лежащие на границе полосы), то ширину полосы можно вычислить как проекцию
вектора
То есть, получаем ширину, умноженную на длину вектора коэффициентов ω. Поэтому, окончательно, имеем:
И эту величину нужно максимизировать. Но для удобства в SVM в знаменателе записывают не длину вектора ω, а квадрат его нормы:
получаем выражение для максимизации ширины:
Принципиально такая замена картины не меняет, но зато мы точно не будем сталкиваться с вычислениями квадратных корней при решении оптимизационной задачи. Наконец, сделаем еще одно, последнее упрощение. Как вы помните из предыдущих занятий, в задачах бинарной классификации вводится понятие отступа (margin):
Эта величина характеризует расстояние от разделяющей гиперплоскости до выбранного образа. Причем:
Но, так как мы рассматриваем случай линейно-разделимых образов, то заведомо существуют такие значения ω и b, что:
Так вот, нам ничто не мешает умножить эту величину на некоторое число:
В результате, получим:
Сути оптимизационной задачи это не изменит. Но зато мы теперь можем подобрать такое значение α и изменить параметры:
чтобы для любых
образов
Строго математически эту нормировку можно записать, следующим образом:
Очевидно, что для линейно-разделимого случая мы всегда можем это сделать. Но тогда автоматически получается, что:
и ширина полосы будет определяться выражением:
В результате для линейно-разделимых образов мы получаем следующую оптимизационную задачу:
Но ее привычно сводят к задаче минимизации:
То есть, нам нужно найти такие ω и b, чтобы минимизировать квадратичную норму весов и вместе с тем обеспечить все отступы больше единицы, кроме тех образов, что лежат непосредственно на границах полосы (там отступ должен быть равен единице). Это называется задачей квадратичного программирования, когда мы минимизируем квадраты весовых коэффициентов при линейных ограничениях неравенствах. Метод опорных векторов для линейно неразделимого случаяОднако, как вы понимаете, в общем случае образы в обучающих выборках редко бывают линейно разделимыми. Поэтому при линейно неразделимой выборке мы не сможем найти параметры ω и b, которые бы удовлетворяли линейным ограничениям на отступы:
Как же быть? Для этого придумали следующую эвристику. Давайте разрешим классификатору ошибаться на некоторую величину (slack variables):
для каждого i-го образа:
Величины slack
variables еще можно воспринимать как некоторый штраф за нарушение исходного
неравенства. Понятно, если все
Это условие мы можем учесть в алгоритме минимизации, записав его, следующим образом:
где C – гиперпараметр,
определяющий степень минимизации величин Все, мы с вами получили эквивалентную задачу оптимизации для общего случая линейно неразделимой выборки. Теперь вопрос, как ее решить? Смотрите, мы можем последние два неравенства в системе переписать в виде:
И, так как мы решаем задачу поиска минимума коэффициентов ω и b, то в этом неравенстве логично выбрать равенство, то есть:
Это выражение еще записывают так:
(положительная срезка – все, что меньше нуля приравнивается нулю). В результате, исходная система становится эквивалентной безусловной задачи минимизации:
или, при делении на параметр C, имеем:
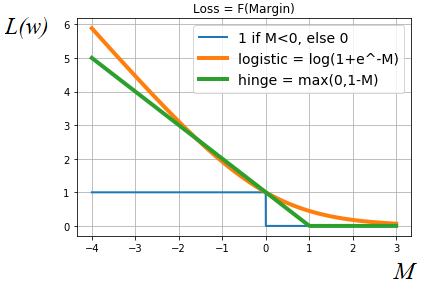
Что вам напоминает это выражение? Да, здесь у нас первым слагаемым идет функционал качества (эмпирический риск), а второе – это L2-регуляризатор для коэффициентов ω. Причем, функция потерь здесь имеет следующий вид (зеленый график) и называется hinge loss.
Для сравнения здесь также приведена логарифмическая функция потерь, которую мы ранее с вами рассматривали. Смотрите, что получается. Фактически, SVM – это решение оптимизационной задачи при функции потерь hinge. Она начинает штрафовать, если минимальный отступ для объекта становится меньше единицы. И никак не штрафует (нулевой штраф), если отступ больше или равен 1. То есть, для hinge loss важна именно ширина полосы между образами двух классов. В отличие, например, от логистической функции потерь, которая стремится максимально развести образы классов относительно разделяющей гиперплоскости, так как здесь штраф постепенно уменьшается при увеличении отступа и никогда не уходит в ноль. Также из метода опорных векторов очень хорошо виден геометрический смысл L2-регуляризатора. Фактически, он здесь отвечает за максимизацию ширины полосы между соседними образами двух разных классов и это в результате приводит к лучшим обобщающим способностям полученного классификатора. На этом мы завершим первое занятие по SVM. Здесь мы получили общий алгоритм для нахождения параметров линейной модели ω и b. На следующем занятии я отмечу подход, с помощью которого можно эффективно решить данную задачу и приведу пример простой реализации метода опорных векторов на Python. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
на вектор
ω:
, лежащих
на границе полосы, величина:
,
то мы можем взять любые веса, например 0 и тогда оптимизационная задача будет
решена. Но, очевидно, это не то, что нам нужно. Конечно, мы разрешаем
ошибаться, но величина этой ошибки должна быть как можно меньше, то есть, нам
нужно найти такие ω и b, чтобы
.
