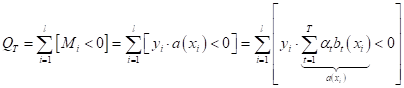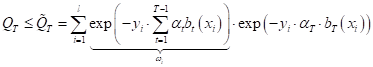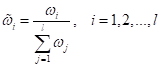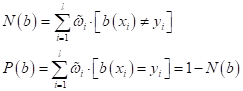|
Введение в бустинг (boosting). Алгоритм AdaBoost при классификацииНа предыдущем занятии мы с вами познакомились с идеей бэггинга (bagging), когда формируется T независимых простых алгоритмов и вычисляется выходное значение в виде усреднения ответов от каждого из них:
Мы подчеркивали, что такой подход будет эффективен, если ответы алгоритмов статистически независимы между собой. Математически это ограничение можно записать так:
Но в этой схеме есть два тонких момента:
Как вы понимаете, это очень жесткие условия и можно считать, что они всегда нарушаются при реализации бэггинга. А значит, мы не достигаем потенциального качества при композиции алгоритмов. Как можно было бы улучшить этот подход? В 1995 году два ученых Йоав Фройнд (Yoav Freund) и Роберт Шапир (Robert Schapire) предложили более общую схему для композиции алгоритмов – с разными весами:
где
Например, в задачах классификации – это может быть величина отступа (margin), который для линейных алгоритмов мы определяли как скалярное произведение:
Или вероятность
принадлежности к тому или иному классу. И так далее. То есть, алгоритмы Итак, при объединении алгоритмов по формуле (1) нам необходимо уметь вычислять весовые коэффициенты и строить набор из T алгоритмов так, чтобы минимизировался заданный показатель качества. Давайте для определенности дальше будем рассматривать задачу бинарной классификации. Тогда показатель качества логично выбрать, как число неверно классифицируемых образов:
Напомню, что
когда отступ для i-го образа меньше нуля ( Обратите
внимание, мы не накладываем никаких жестких ограничений на алгоритмы Глядя на полученный функционал качества, мы понимаем, что его нужно оптимизировать и по весовым коэффициентам и по алгоритмам:
Но это довольно сложная математическая задача, поэтому Фройнд и Шапиро предложили использовать следующие две эвристики:
Эти два подхода положены в основу практически всех алгоритмов бустинга (boosting). То есть, мы пытаемся построить T относительно простых алгоритмов (классификации или регрессии), а затем вычислить взвешенную сумму их выходов для улучшения результирующего значения в соответствии с выбранным показателем качества. Это и есть смысл бустинга алгоритмов. Алгоритм AdaBoostЧтобы все это
лучше понять, рассмотрим конкретный пример – алгоритм AdaBoost (сокращение от Adaptive Boosting), который и
предложили Фройнд с Шапиро применительно к задачам бинарной классификации с
метками классов
Если расписать это выражение, то получим выражение:
Теперь,
смотрите. Согласно первой эвристике, мы будем искать наилучший алгоритм
Обе формулы –
одно и то же, но во второй мы явно (отдельно) вынесли Давайте
проанализируем и посмотрим, какой смысл имеют эти веса. Во-первых, они
вычисляются для каждого объекта Далее, по
алгоритму, веса
То есть, мы делаем так, чтобы в сумме нормированные веса давали единицу:
Благодаря этому,
они не будут уходить в ноль или в бесконечность, а принимать вполне разумные
значения. Это важно при реализации алгоритма на компьютере. В итоге для каждого
текущего алгоритма
Очевидно, лучший текущий алгоритм должен минимизировать долю неверных классификаций:
(это соответствует
выбранному показателю качества). И далее, Фройнд с Шапиро доказали, что
наилучшее (оптимальное) значение весового коэффициента при экспоненциальной
функции потерь и найденного алгоритма
Все, это и есть
основа алгоритма AdaBoost. Фактически, мы на каждой итерации (от
1 до T) обучаем
текущий алгоритм Сейчас мы в
деталях посмотрим на работу этого алгоритма, когда в качестве алгоритмов Вход: обучающая
выборка Выход: набор базовых
алгоритмов 1: начальная
инициализация весов объектов: 2: для
всех
3: найти наилучший текущий алгоритм по правилу:
4: вычислить оптимальный коэффициент:
5: обновить веса объектов:
6: нормировать веса объектов:
Реализация алгоритма AdaBoost для задачи классификации на PythonА теперь, как и
обещал, приведу реализацию алгоритма AdaBoost на Python с
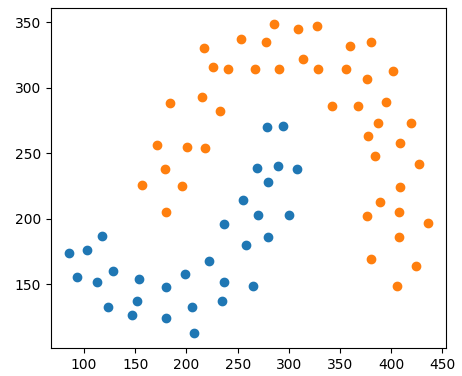
использованием решающих деревьев в качестве базовых алгоритмов Предположим, у нас имеется обучающая выборка в виде следующего набора точек двух классов:
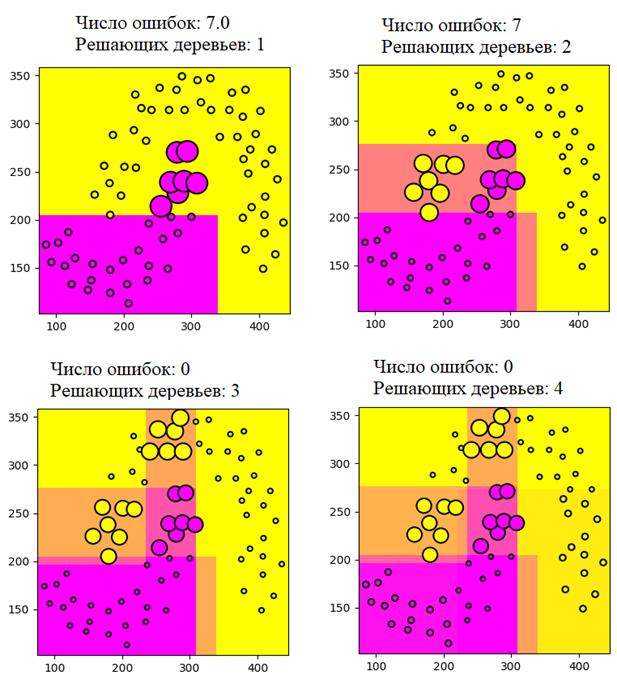
Мы будем их разделять (классифицировать) композицией из T деревьев глубиной два. Программу можно скачать по адресу: machine_learning_42_adaboost_classification.py В итоге, получаем следующие результаты:
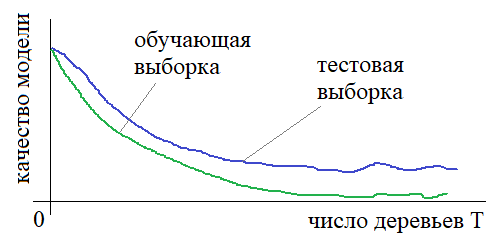
Ожидаемо, что при увеличении числа деревьев в композиции, число ошибок также уменьшается. При этом, мы использовали очень простые деревья уровня два. Каждое из них по отдельности не смогло бы справиться с задачей, но в композиции получается безошибочная классификация на обучающей выборке. И, возможно, здесь у вас появится вопрос. Раз алгоритм так хорошо подстраивается под обучающую выборку, то возможно он переобучился и на тестовых данных будет показывать значительно худшие результаты? Именно так предполагали в самом начале появления бустинга и считали, что чем больше взять алгоритмов в композиции, тем сильнее он будет подстраиваться под обучающую выборку и, соответственно, сильнее переобучаться. Но к удивлению исследователей картина оказалась кардинально иной: даже при очень большом числе алгоритмов (порядка 1000) переобучение практически не проявляется и композиция в целом демонстрирует хорошие обобщающие способности на новых тестовых данных.
То есть бустинг ведет себя также как и бэггинг при увеличении числа алгоритмов. И это очень здорово! Это значит, мы можем получать очень хорошие результаты классификации или регрессии просто увеличивая число простых алгоритмов, входящих в бустинг. Благодаря этому свойству он приобрел очень широкую популярность и является буквально настольным инструментов инженеров в области машинного обучения. Например, знаменитый Матрикснет от компании Яндекс использует бустинг над решающими деревьями для формирования ранжирования в поисковой выдаче. Правда там используется алгоритм не AdaBoost, а более совершенная техника. Но о некоторых этих аспектах мы поговорим уже на последующих занятиях. Видео по теме |
все
же выдают несколько зависимые значения (в общем случае, полной независимости
достичь невозможно);
,
то есть, значимость каждого полагается равной.
(1)
-
веса (положительные числа); 
-
простые алгоритмы обработки входного вектора 
.
Причем, будем полагать, что алгоритмы выдают вещественное значение:
),
значит произошла ошибка классификации и квадратные скобки (нотация Айверсона)
вернут 1. Иначе возвращается 0.
и
весового множителя 
при
фиксации ранее найденных алгоритмов и весовых множителей: 
и
.
То есть, на каждом шаге t мы вычисляем
только один весовой коэффициент 
.
Для аппроксимации порогового функционала качества было предложено использовать экспоненциальную
функцию потерь:
и
вес 
при
фиксированных предыдущих алгоритмах 
и
весах 
.
Поэтому перепишем функционал качества 
,
следующим образом:
.
И перед второй экспонентой появляется множитель (вес) 
,
так как предыдущие алгоритмы и коэффициенты зафиксированы.
обучающей
выборки, то есть, это, фактически, веса объектов. Во-вторых, множитель будет
тем больше, чем более отрицательным будет отступ (margin). То есть,
множитель возрастает для плохо классифицируемых объектов. В результате, текущий
алгоритм 
нормируются
при поиске каждого следующего алгоритма по формуле:
мы
легко можем подсчитать долю верных и неверных классификаций:
на
взвешенных объектах обучающей выборки. Само обучение выполняется любым
известным нам способом. А, затем, для него вычисляется коэффициент 
.
выступают
решающие деревья. Но вначале я приведу псевдокод общего алгоритма AdaBoost:
и
параметр T (число
алгоритмов в композиции)
с
весами 
