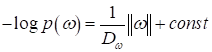|
Вероятностный взгляд на L1 и L2-регуляризаторыПрактический курс по ML: https://stepik.org/course/209247/ На предыдущем занятии мы с вами сделали первый шаг в вероятностную интерпретацию задач машинного обучения. Увидели, как с помощью модели под названием логистическая регрессия, можно не только делать прогноз класса, но и вычислять уверенность (вероятность) классификатора в этом прогнозе. Вообще вероятностный (точнее, байесовский) подход к машинному обучению – это большая, объемная научная область, которую мы лишь слегка коснемся. В частности, посмотрим на уже знакомые нам L1 и L2-регуляризаторы с вероятностной точки зрения. Начнем с того, что я напомню, мы строили прогноз в логистической регрессии, как вероятность правильной классификации:
При этом метки
для классов должны принадлежать множеству
И, так как мы
предполагаем, что выходы зависят от настраиваемого вектора параметров
А задача поиска
оптимального вектора
Это и есть общая
вероятностная постановка задачи для оптимизации (нахождения) коэффициентов
Я здесь учитываю
тот факт, что входные объекты (наблюдения)
Это есть не что
иное, как теорема Байеса для условной ПРВ. Она позволяет выполнять пересчет
вероятностей выходов
Однако, на
предыдущем занятии нам повезло, так как
Эти небольшие теоретические выкладки, что я привел, показывают, как важно опираться на строгие математические выводы, а не просто на «здравый смысл». Но я все это привел еще и для того, чтобы вы увидели ключевой вероятностный элемент задач машинного обучения – формулу Байеса. Часто, именно она является отправной точкой для решения оптимизационных задач с позиции теории вероятностей. В частности, так обстоит дело с L1 и L2-регуляризаторами. Давайте
вспомним, что регуляризация – это ограничения, накладываемые на значения
вектора коэффициентов
А как можно в вероятностном смысле интерпретировать эти ограничения? Да, через априорную ПРВ для параметров ω. В частности, L2-регуляризатор соответствует нормальному распределению:
где Теперь, с учетом наличия априорной ПРВ для вектора параметров, нам следует рассматривать оптимизацию следующей совместной ПРВ:
Снова распишем эту формулу, получим:
и алгоритм поиска наилучших параметров, будет иметь вид:
Мы здесь
отбросили Что же в итоге имеем? Давайте предположим, что у нас имеется некая обучающая выборка для задачи бинарной классификации:
Тогда подбор параметров по обучающей выборке можно записать так, как мы это делали на предыдущем занятии:
То есть, мы здесь используем логарифм правдоподобия. Это эквивалентно, следующей функции потерь:
В свою очередь:
(здесь const=0, т.к. не
влияет на оптимизацию). И, как раз, приходим к выражению L2-регуляризации,
которое мы ранее с вами вводили из некоторых эвристических соображений. Здесь
же мы точно, математически показали, что L2-регуляризатор
эквивалентен введению нормального априорного распределения на вектор
настраиваемых параметров. Причем, предполагается, что элементы вектора
можно определять
L2-регуляризатор
с произвольной корреляционной матрицей По аналогии распишем вероятностно L1-регуляризатор. Там используется сумма модулей и это приводит нас к распределению Лапласа:
где
но второе слагаемое будет несколько иным:
(здесь также const=0). В приведенной формуле распределения Лапласа мы также полагаем независимость элементов вектора параметров, нулевое среднее и постоянную дисперсию. Если же это не так, то опираясь на формулу, всегда можем скорректировать поведение L1-регуляризатора.
Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
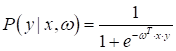
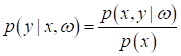
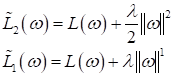
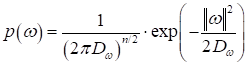 ,
,
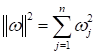 ;
;
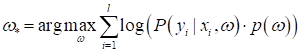
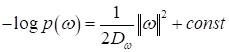
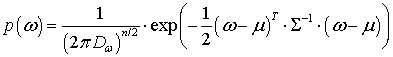
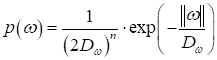
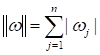 .
В этом случае функция потерь принимает тот же вид:
.
В этом случае функция потерь принимает тот же вид: