Вероятностная оценка качества моделей

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

На предыдущих занятиях мы с вами познакомились с несколькими подходами для решения задач бинарной классификации, в том числе:

логистическая регрессия;
метод опорных векторов.

Во всех случаях мы имеем некую параметрическую модель:

которая выдает метки классов:

и позволяет вычислить отступ для объектов обучающей или тестовой выборок:

Например, для линейных моделей, отступ определяется обычным скалярным произведением:

Имея эти данные, нам бы хотелось уметь оценивать качество полученной модели. Конечно, вы сейчас можете сказать, что нет ничего проще: давайте, например, посмотрим на долю верной классификации в отложенной (тестовой) выборке (метрика accuracy):

И она действительно покажет, как часто классификатор давал верные ответы на тестовых данных. Например, если вся выборка k = 1000, а модель сделала 10 ошибок, то accuracy составит:

Но это число ничего не говорит, по крайней мере, о двух важных аспектах:

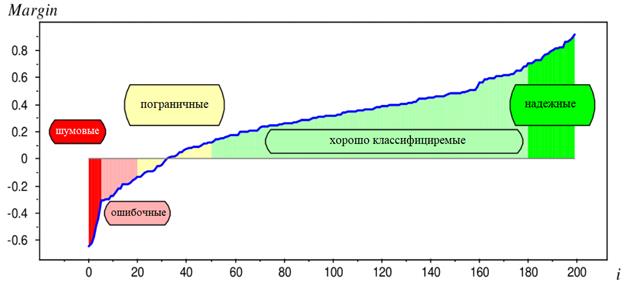
насколько модель была уверена в своих прогнозах;
насколько была сбалансирована выборка при вычислении accuracy.

Начнем с первого аспекта. Как можно определить уверенность классификатора в своем ответе? Наверное, в самом простом случае, можно построить распределение отступов:

для всех объектов отложенной выборки:

Если график имеет «быстрый» переход через ноль с минимальной зоной пограничных объектов, то, очевидно, такой классификатор должен давать надежные оценки и иметь хорошую обобщающую способность. Если желтая область пологая и содержит много пограничных объектов, то это повод задуматься о надежности модели и, возможно, попробовать другие алгоритмы для решения текущей задачи.

Но это чисто визуальный метод оценки надежности модели, хотя и очень неплохой. Однако, в ряде задач нам бы хотелось получать численные характеристики уверенности модели в правильной классификации. И, как это сделать мы с вами уже говорили, когда рассматривали вероятностный взгляд на задачи машинного обучения. В частности, для логистической регрессии при функции потерь:

было явно показано, что величину отступа (линейной модели):

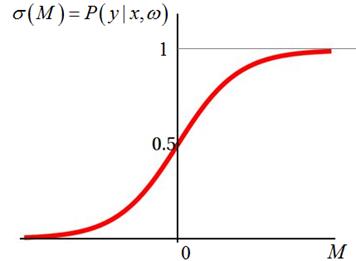
можно перевести в значения вероятности с помощью сигмоидной функции:

Но насколько эта вероятность будет соответствовать действительности? То есть, если уверенность модели в прогнозе составляет, например, 0,7, то, в принципе, мы ожидаем, что этот прогноз будет сбываться в 70% случаях. Например, модель оценивает заемщиков и решает, кому дать кредит (метка класса +1), а кому отказать (метка класса -1). Предположим, она выдает прогноз +1 со значением вероятности 0,9. Значит, мы ожидаем, что 90% таких заемщиков будут отдавать кредит. И здесь важно, чтобы это значение как можно точнее совпало с реальным поведением заемщиков. Иначе банк не сможет корректно просчитать свои риски. Поэтому, это далеко не праздный вопрос.

Так как нам убедиться в корректности вероятностного значения? Обычно, это делают по отложенной (тестовой) выборке. Весь вероятностный диапазон [0; 1] разбивают на поддиапазоны:

Затем, перебирают все k объектов тестовой выборки, вычисляя для каждого вероятность:

После этого объект помещается в соответствующий поддиапазон:

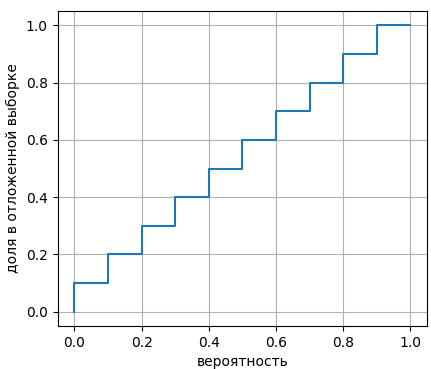
В результате, мы для каждого вероятностного интервала вычисляем долю объектов, которые в него попали:

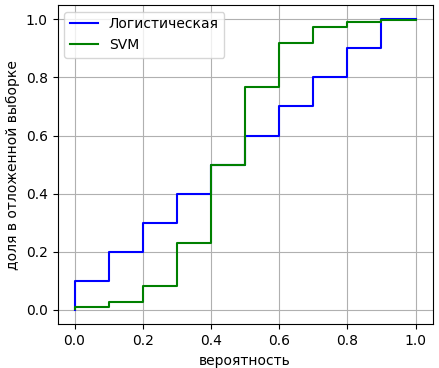
Если получается примерно диагональный график, значит, расчетные вероятности соответствуют экспериментальным показаниям и таким значениям можно доверять. В частности, логистическая регрессия, как правило, дает такой диагональный график, поэтому отступы ее модели можно совершенно спокойно пересчитывать в вероятности и пользоваться этими значениями в дальнейшем.

А вот если построить аналогичный график для метода опорных векторов, то, как правило, получается следующая картина:

Здесь зеленый график несколько перекошен относительно диагонали (синего графика). Это значит, что отступы в SVM не могут быть напрямую переведены в вероятности. Получается, что мы не можем использовать вероятностную интерпретацию выходов модели в случае метода опорных векторов? Напрямую да, не можем. Но можно сделать калибровку кривой: приведение расчетных вероятностей к экспериментальным значениям. Например, мы видим, что для диапазона [0,3; 0,4) экспериментальная вероятность составляет примерно 0,2. Значит, значения вероятностей этого диапазона надо заменять на 0,2. И так для всех интервалов. Такие калибровки действительно проводят и это нормальная практика.

Теперь мы с вами знаем, что вероятности, которые можно рассчитать для моделей, необходимо проверять по отложенной выборке. И, при необходимости, проводить калибровку этих значений.

На этом мы завершим текущее занятие, а на следующем продолжим эту тему и рассмотрим методы оценок надежности моделей при несбалансированных выборках.

Практический курс по ML: https://stepik.org/course/209247/

Вероятностная оценка качества моделей

Видео по теме