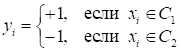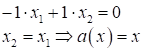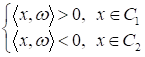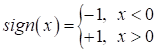Линейные модели. Градиентный алгоритм
Что такое машинное обучение? Обучающая выборка и признаковое пространство
Постановка задачи машинного обучения
Линейная модель. Понятие переобучения
Способы оценивания степени переобучения моделей
Уравнение гиперплоскости в задачах бинарной классификации
Решение простой задачи бинарной классификации
Функции потерь в задачах линейной бинарной классификации
Стохастический градиентный спуск SGD и алгоритм SAG
Пример использования SGD при бинарной классификации образов
Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam
L2-регуляризатор. Математическое обоснование и пример работы
L1-регуляризатор. Отличия между L1- и L2-регуляризаторами
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
Линейные модели. Градиентный алгоритм

Уравнение гиперплоскости в задачах бинарной классификации

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

С этого занятия мы начнем изучение довольно интересной темы в машинном обучении – классификации входных наблюдений. Подобные алгоритмы нас сейчас окружают повсюду – это и камеры с функцией распознавания лиц, походки, чрезвычайных ситуаций и т.п., распознавание отпечатка пальца владельца смартфона, доступ к защищенным данным по радужной оболочке глаза и голосу и масса других приложений. Но, какими бы сложными они ни казались на первый взгляд, в их основе часто лежит общий, простой принцип – построение разделяющей гиперплоскости в определенном признаковом пространстве.

Давайте, для простоты, поставим задачу двухклассовой классификации точек на плоскости, которые линейно разделимы. В этом случае каждый входной вектор будет иметь два измерения:

А целевые выходные значения – одно из двух значений:

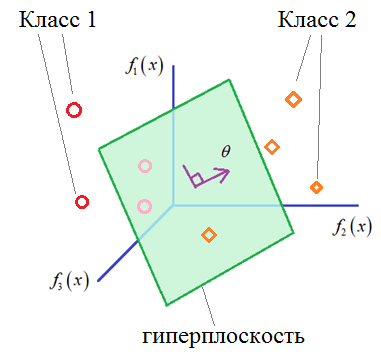
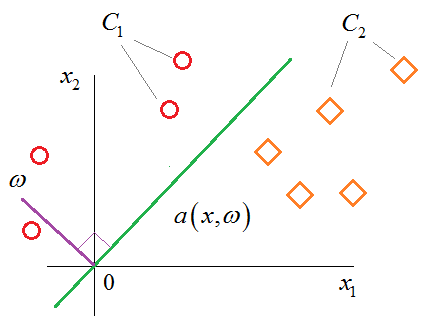
Графически, распределение двух классов можно представить, следующим образом:

В качестве модели в этой задаче выступает уравнение разделяющей прямой:

Давайте теперь зададимся вопросом, что это за множество точек, лежащих на прямой ? Очевидно, это точки, у которых координаты связаны выражением:

Распишем его, получим:

И в общем виде можно записать, следующим образом:

Смотрите, что здесь получается. Если выделить два вектора:

то эту же формулу можно переписать в виде:

Здесь - скалярное произведение двух векторов. А свободный коэффициент лишь определяет смещение прямой по оси ординат. Давайте пока его приравняем нулю и будем считать, что прямая проходит через начало координат. А в качестве вектора

, то есть

При этих параметрах получаем следующее уравнение прямой:

То есть, это прямая, которая проходит под 45 градусов через начало координат, а вектор ортогонален этой прямой:

Можно заметить, что вектор всегда ортогонален разделяющей прямой , так как, вспоминая школьную математику, скалярное произведение можно расписать и так:

Если длины векторов отличны от нуля (как в нашем случае) , то получаем косинус угла между ними равный нулю. А это справедливо только для ортогональных векторов, то есть, при .

Картина не изменится если свободный коэффициент . В этом случае прямая будет вращаться не относительно точки 0, а в точке выше или ниже по оси ординат. Главное, что здесь по-прежнему векторы (остаются ортогональными друг другу).

Это очень важный момент при решении задач классификации входных данных с помощью линейной модели:

И вы сейчас увидите почему. Но вначале отмечу, что вот этот свободный член также можно внести в скалярное произведение, если исходные двумерные векторы дополнить третьим измерением с константным значением -1:

Тогда вектор принимает вид:

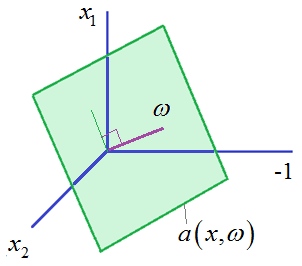
и мы получаем уравнение множества точек на плоскости в трехмерном пространстве:

Как видите, здесь по-прежнему векторы и графически все можно представить, следующим образом:

Причем, гиперплоскость в трехмерном пространстве признаков будет вращаться относительно нуля, хотя изначально в двумерном у нас было смещение по оси ординат. Этот пример хорошо показывает, что для любого вектора размерности n мы всегда можем добавить одно новое измерение, чтобы сформировать гиперплоскость, проходящую через ноль.

Хорошо, мы с вами поняли, как описывается разделяющая гиперплоскость в задачах классификации линейно разделимых образов и что вектор параметров , который ее задает, всегда перпендикулярен этой плоскости. Но, как нам теперь, используя эту модель , отделять объекты одного класса от другого? Делается это очень просто. Давайте я покажу это на примере двумерного пространства, но та же самая идея будет применима к пространству любой размерности.

Смотрите, если модель сформирована верно и линия действительно делит образы на два класса, то для любой точки первого класса скалярное произведение с вектором параметров будет положительным, а для точек класса - отрицательным:

Почему так происходит, хорошо видно из рисунка. Радиус-векторы точек для класса образуют острый угол с вектором . Так как скалярное произведение – это, фактически, вычисление косинуса угла между векторами, то для острых углов будем получать положительные значения. Точки же класса образуют тупые углы с вектором . Следовательно, для них будем иметь отрицательные значения. Видите, как математически можно очень просто разделить точки, лежащие по разные стороны от прямой или гиперплоскости, т.к. в многомерном пространстве признаков мы будем иметь тот же самый принцип.

В итоге, алгоритм классификации образов с помощью модели можно записать в виде:

Здесь sign() – знаковая функция, которая возвращает +1 для положительных чисел и -1 – для отрицательных:

Вы можете спросить, а что делать, если скалярное произведение даст точно 0. В нуле эта функция не определена. На самом деле, в практике, вероятность того, что точка окажется точно на разделяющей гиперплоскости, почти равна нулю. Но для надежности мы можем положить, что если окажется:

то выдаем отказ в классификации (значение 0), т.к. здесь действительно неясно, к какому классу отнести данный образ.

Надеюсь, из этого занятия вы поняли, как задается гиперплоскость и как с ее помощью выполняется бинарная классификация векторов входных наблюдений.

Практический курс по ML: https://stepik.org/course/209247/

Уравнение гиперплоскости в задачах бинарной классификации

Видео по теме