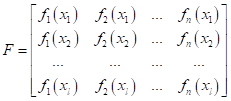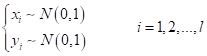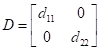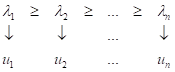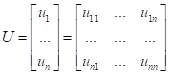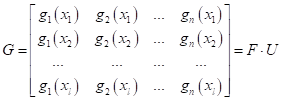|
Сингулярное разложение и его связь с PCAПрактический курс по ML: https://stepik.org/course/209247/ Практическое использование метода главных компонент (PCA – Principal Component Analysis) тесно связано с сингулярным разложением матриц (Singular Value Decomposition, SVD), которое формально записывается так:
На первый взгляд эта формула выглядит совершенно непонятной и странной. В конце концов, зачем нам раскладывать матрицу на произведение трех других? Но не спешите делать такие заключения. Эта формула – одно из значимых практических достижений линейной алгебры и довольно часто применяется в алгоритмах машинного обучения. Здесь каждая матрица имеет свой особый смысл. И сейчас вы узнаете, как она «работает». Пусть матрица F – это матрица объектов в признаковом пространстве:
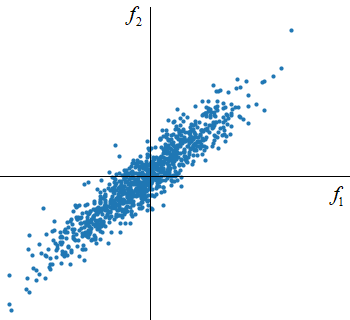
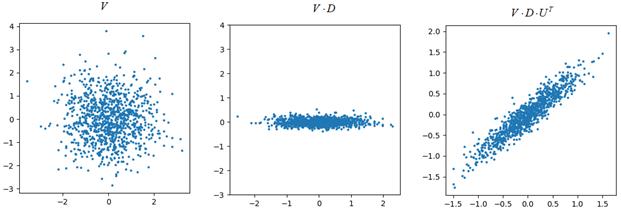
Для простоты изобразим множество точек объектов матрицы F на плоскости (двумерном пространстве):
В действительности, для получения такого распределения, я сначала сгенерировал координаты множества точек по нормальному закону с нулевым средним и единичной дисперсией:
Получил матрицу:
Затем, изменил масштаб проекций точек по обеим координатам с использованием диагональной матрицы
А в конце
повернул исходную систему координат на 45 градусов, используя матрицу поворота
В результате, мы представили точки исходного признакового пространства через произведение трех матриц:
Это и есть графическая интерпретация сингулярного разложения. Однако остается вопрос, зачем все это нужно? Применений, на самом деле, множество. Я покажу то, что нас сейчас больше всего интересует: связь сингулярного разложения с методом главных компонент. Связь сингулярного разложения с PCAКогда мы вычисляли (на предыдущих занятиях) собственные векторы и собственные значения матрицы:
то получали
упорядоченный набор векторов
Эти векторы, как вы уже знаете, образуют ортонормированный базис (систему координат в новом признаковом пространстве). Если их записать в виде матрицы:
То исходные точки (признаки) матрицы F в новом базисе U будут иметь представление:
А обратное
преобразование из G в F, запишется в виде (при условии, что
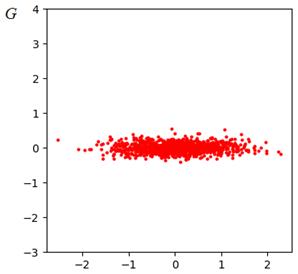
Фактически, здесь, матрицу U можно воспринимать, как матрицу поворота. Именно она ориентирует новую ортонормированную систему координат вдоль наиболее значимых изменений координат признаков. И если мы отобразим новые полученные признаки G:
То никакого поворота множества точек уже не будет, т.к. мы как бы находимся внутри повернутой системы координат U. А вот масштаб вдоль каждой из осей, разный. Но мы знаем, что разброс проекций на каждую ось, определяется соответствующим собственным числом λ, причем λ – это дисперсия разброса. Отсюда получаем, что диагональная матрица масштабирования, может быть записана в виде:
И матрица
где V – матрица распределения признаков в пространстве U без искажения масштаба по осям (с равным масштабом). Отсюда автоматически получаем, что исходное признаковое пространство F может быть представлено в виде:
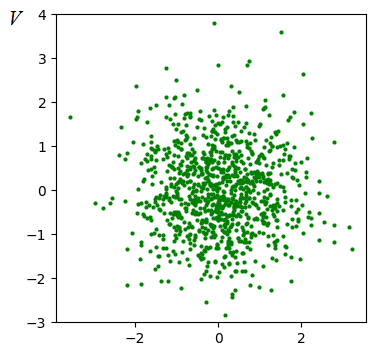
А это и есть формула сингулярного разложения. Получается, что когда мы вычисляли собственные векторы (матрицу U) и собственные значения (диагональную матрицу Λ), то, по сути, шли по пути сингулярного разложения матрицы F. Последнюю матрицу V мы могли бы вычислить как:
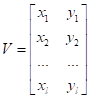
И в нашем примере распределение точек матрицы V имело бы вид:
Как видите, здесь мы просто устранили искажение по обеим осям, привели все к единому масштабу. Ну, хорошо, мы увидели, что сингулярное разложение и метод главных компонент – это, фактически, одно и то же. Но, что это нам дает? Главное здесь то, что сингулярное разложение имеет более эффективный вычислительный алгоритм, чем прямой поиск собственных векторов и чисел. Поэтому, для реализации метода главных компонент часто выполняют сингулярное разложение, а затем, применяют метод PCA. Так рекомендуется делать при больших размерностях признакового пространства (от тысяч и более). Сокращение числа признаков в разреженных матрицах с помощью SVDВ машинном обучении часто встречаются задачи, приводящие к матрицам признаков с большим количеством нулевых значений. Например, при разработке рекомендательных систем. Предположим, на некотором сервисе пользователи ставят лайки под видео. Это можно представить в виде следующей матрицы исходных признаков:
Такие разреженные матрицы часто имеют ранг (максимальное число линейно независимых строк или столбцов) гораздо меньший размерности самой матрицы. В этом случае можно применить сингулярное разложение для сокращения признакового пространства и формирования нового, где эта разреженность будет отсутствовать:
Тогда мы получим большое количество нулевых собственных чисел и соответствующие признаки в пространстве U можно просто отбросить. Благодаря этому ускоряется алгоритм обучения и повышаются обобщающие способности полученной модели. Вообще, если вы будете активно заниматься разработкой алгоритмов машинного обучения (или уже этим занимаетесь), то метод SVD вам, наверняка, пригодится и не раз. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |