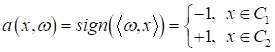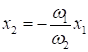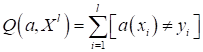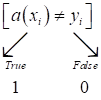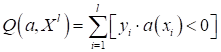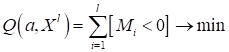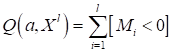|
Решение простой задачи бинарной классификацииПрактический курс по ML: https://stepik.org/course/209247/ На этом занятии я хочу привести простой пример решения задачи бинарной классификации линейно разделимых образов. Это позволит вам лучше понять специфику решения подобных задач. Напомню, что на предыдущем занятии мы с вами определили, следующий алгоритм бинарной классификации:
где Предположим, мы хотим создать классификатор, который бы отличал гусениц от божьих коровок по двум результатам измерений: ширины и длины. В итоге, наша обучающая выборка будет состоять из следующих наблюдений:
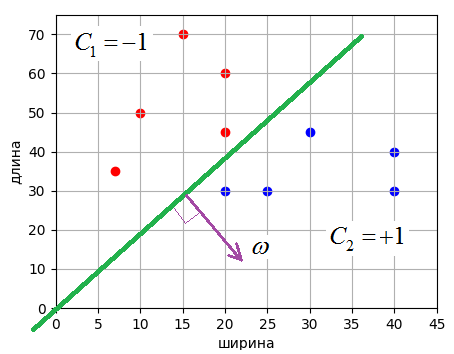
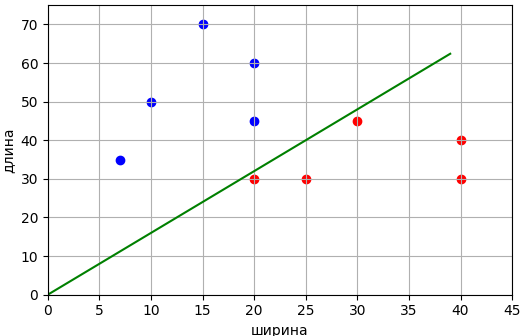
Визуально множество измерений располагается, следующим образом:
Здесь красными точками отмечены гусеницы, а синими – божьи коровки. Причем, гусеницам будет соответствовать целевое значение -1, а божьим коровкам – +1. Также видно, что обучающая выборка образует линейно-разделимые классы и разделяющую линию можно провести через начало координат. Поэтому уравнение линии будем искать в виде:
Упростим выражение, перепишем его, следующим образом:
Если принять
А общий вектор:
Фактически,
здесь Примерно в середине 1950-х годов подобную задачу решал Фрэнк Розенблатт. Он сформулировал критерий качества для разделяющей линии как число неверных классификаций:
Здесь квадратные скобки – это индикатор ошибки, они переводят булевы величины True и False в значения 1 и 0 (нотация Айверсона):
В данном случае,
если ответ решающего правила Однако, при
решении задач бинарной классификации, когда целевые ответы выбираются из
множества
Здесь величина Такое произведение очень часто используют при разработке алгоритмов бинарной классификации. Обозначают его большой буквой M:
и называют отступом (в переводе с англ. margin). Эта величина может показывать не только признак верной классификации, но и насколько далеко отстоит образ от разделяющей плоскости. В нашем случае мы могли бы измерять это расстояние, если убрать знаковую функцию из модели:
и
Но пока нам это не нужно и мы оставим функцию sign(). Главное здесь запомнить, как вычисляется margin и что он означает. В дальнейшем мы его будем активно использовать. Итак, критерий качества для решения поставленной задачи сформулирован:
Как нам теперь
им воспользоваться, чтобы найти коэффициент
1) инициализация 2) повторять N раз 3) поочередно
выбирать 4) если 5)
корректировать вес: 6) вычисляем
показатель качества 7) если Реализацию на Python этой задачи можно посмотреть в файле После запуска программы увидим следующий результат:
Как видите, нам
удалось построить разделяющую линию для выборки из двух классов. Конечно, это
относительно простая задача. Здесь я лишь хотел показать принцип обучения
алгоритма по тренировочной выборке, а также познакомить с понятием отступа (margin) и критерием
качества Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
-
вектор настраиваемых (в процессе обучения) параметров. Как искать вектор 
-
это ключевой вопрос таких задач. На этом занятии мы будем действовать банально,
прямолинейно, что называется «в лоб» для нахождения значений компонент вектора 
,
то останется только один подбираемый параметр:
-
угловой коэффициент прямой и нам нужно его найти.
не
совпадает с целевым 
,
то формируется значение True, то есть, 1. И, наоборот, при
совпадении, будем получать False и значение 0. В итоге, функционал 
будет
подсчитывать число ошибок классификации.
,
тот же самый показатель качества можно вычислить и так:
будет
принимать отрицательные значения при ошибочных классификациях и положительные –
при правильных. Действительно, если знаки величин 
совпадают,
значит, мы верно отнесли образ к нужному классу и произведение будет
положительным. Иначе, знаки будут различаться, и произведение будет меньше нуля.
,
шаг обучения 
, максимальное
число итераций N
из
обучающей выборки 
, то
,
то прерываем цикл (решение найдено)
