Решающие деревья
Логические методы классификации
Критерии качества для построения решающих деревьев
Построение решающих деревьев жадным алгоритмом ID3
Усечение (prunning) дерева, обработка пропусков и категориальных признаков
Решающие деревья в задачах регрессии. Алгоритм CART
Случайные деревья и случайный лес. Бутстрэп и бэггинг
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
Решающие деревья

Решающие деревья в задачах регрессии. Алгоритм CART

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

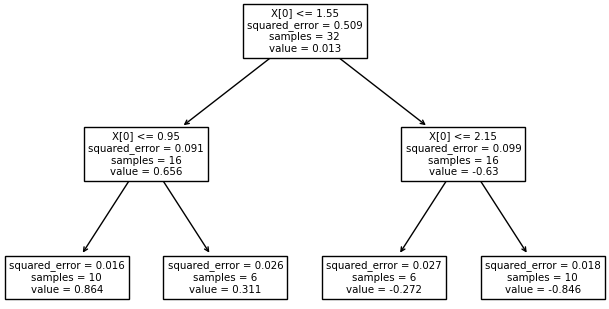
На предыдущих занятиях мы с вами рассматривали решающие деревья для задач классификации. Однако, в ряде случаев, их применяют и для задач регрессии, когда алгоритм на выходе формирует одно вещественное значение (или несколько значений) для каждого входного вектора . То есть, в листьях такого дерева хранятся соответствующие вещественные числа.

Давайте, для определенности, я сразу приведу пример такого решающего дерева.

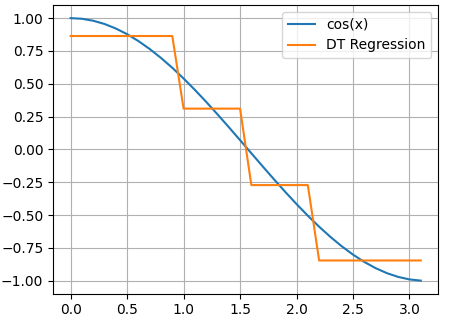
Смотрите, изначально наши данные представляют собой точки функции cos(x):

Здесь аргумент функции cos() – это признак, а значения функции в каждой точке – целевые переменные. Затем, по признаку (аргументу функции) выполняется разделение исходного множества точек на непересекающиеся подмножества. В результате, при глубине дерева два, получаем четыре подинтервала и четыре листа. Причем, в каждом листе хранится одно константное вещественное значение, которым заменяются все значения выделенного подмножества. Поэтому мы видим на графике ступенчатую функцию при аппроксимации косинусоиды решающим деревом.

Вот общая идея использования решающих деревьев для задач регрессии. И здесь возникают два главных вопроса:

По какому критерию оценивать качество деления на подмножества (то есть, что использовать в качестве меры неопределенности – impurity)?
Как вычислять вещественные значения в полученных листовых вершинах?

Хорошая новость, что на оба этих вопроса имеется единый ответ. Я начну с последнего. Часто в задачах регрессии требуется обеспечить минимум среднеквадратичной ошибки прогноза:

Здесь - ответ (прогноз) модели на входной вектор признаков ; - множество объектов , дошедших до некоторой листовой вершины v, и соответствующие им целевые значения .

Так как при использовании решающих деревьев каждое подмножество аппроксимируется некоторым константным значением:

то для минимизации квадратичного критерия, величину следует вычислять, как среднее арифметическое от всех целевых значений , попавших в листовую вершину v дерева:

Можно легко доказать, что эта величина будет наилучшим образом описывать значения подмножества при квадратичном критерии.

Так как величина зависит от множества , а значит, от способа разбиения деревом исходной обучающей выборки, то ее было бы логично использовать в качестве меры информативности (impurity) и выбирать в каждой промежуточной вершине разбиение так, чтобы максимизировался информационный выигрыш:

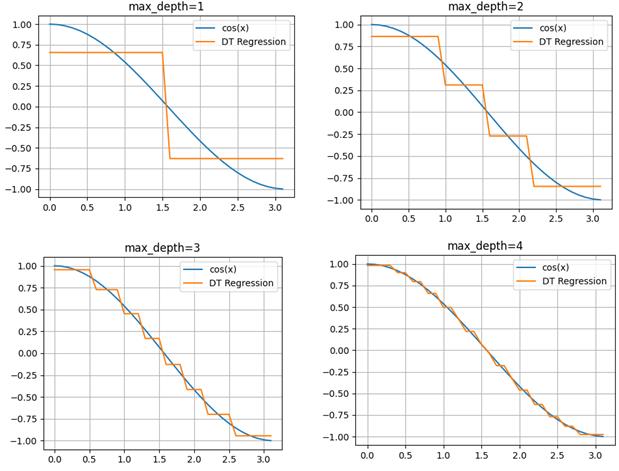
То есть, мы будем выбирать порог t так, чтобы impurity левого и правого подмножеств были как можно меньше.

Вот примеры разбиения исходной последовательности деревом глубиной от единицы до четырех:

Как видите, вначале выделяются два равных подмножества и две константы, которые грубо описывают график косинусоиды. И это описание наилучшее с точки зрения квадратического критерия. При увеличении глубины, получаем все больше и больше информации об исходном сигнале, и для глубины 4 вполне угадывается график косинусоиды.

Реализация решающих деревьев на Python с помощью Scikit-Learn

Итак, мы с вами в целом познакомились с идеей решающих деревьев для задач классификации и регрессии. Осталось узнать, как можно реализовать эти подходы при решении практических задач. В самом простом варианте это можно сделать на языке Python с использованием библиотеки Scikit-Learn. В этой библиотеке имеется ветка:

from sklearn import tree

которая отвечает за построение решающих деревьев.

Разработчики Scikit-Learn использовали алгоритм:

Classification and Regression Trees (CART)

с помощью которого можно выполнять как классификацию, так и решать задачи регрессии. Подробнее об этом можно почитать на странице официальной документации:

https://scikit-learn.org/stable/modules/tree.html

Давайте, вначале построим решающее дерево для задачи регрессии. Для этого сформируем обучающее множество в виде значений функции косинуса:

import numpy as np
import matplotlib.pyplot as plt
 
x = np.arange(0, np.pi, 0.1).reshape(-1, 1)
y = np.cos(x)

И, затем, по этому набору данных построим решающее дерево с максимальной глубиной 3:

clf = tree.DecisionTreeRegressor(max_depth=3)
clf = clf.fit(x, y)

После этого выполним прогноз по значениям x:

yy = clf.predict(x)

и отобразим полученные графики (результаты):

plt.plot(x, y, label="cos(x)")
plt.plot(x, yy, label="DT Regression")
plt.grid()
plt.legend()
plt.show()

Вот так достаточно просто используются решающие деревья, применительно к задачам регрессии. Дополнительно можно вывести структуру полученного дерева с помощью команды:

tree.plot_tree(clf)

По умолчанию класс DecisionTreeRegressor использует критерий минимума квадрата ошибки прогноза так, как мы говорили на этом занятии. Но, при необходимости, можно воспользоваться и другим критерием – минимума модуля ошибки прогноза. Подробно об этом написано в официальной документации (по ссылке, что приведена выше). Дополнительно у класса DecisionTreeRegressor имеются и другие параметры для управления построением дерева. Все это можно посмотреть в документации.

Решающие деревья для задач классификации

При решении задач классификации используется класс DecisionTreeClassifier библиотеки Scikit-Learn:

from sklearn.tree import DecisionTreeClassifier

У него также много разных входных параметров для управления построением дерева. Обо всем подробно можно почитать в официальной документации. Здесь же отмечу, что по умолчанию используется критерий Джини в качестве impurity и методика усечения дерева (pruning).

Давайте применим этот класс для разделения цветков ирисов по видам. Программу можно посмотреть по адресу:

machine_learning_40_classification.py

Думаю, из этих занятий у вас сложилось общее представлении об идее решающих деревьев для задач классификации и регрессии.

Практический курс по ML: https://stepik.org/course/209247/

Решающие деревья в задачах регрессии. Алгоритм CART

Реализация решающих деревьев на Python с помощью Scikit-Learn

Решающие деревья для задач классификации

Видео по теме