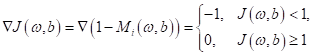Реализация метода опорных векторов (SVM)

Практический курс по ML: https://stepik.org/course/209247/

На предыдущем занятии мы с вами рассмотрели оптимизационную задачу для метода опорных векторов, получили следующую систему:

              (*)

и из нее пришли к алгоритму для поиска параметров ω и b:

Для минимизации этого функционала обычные градиентные методы нам не подходят, т.к. функция потерь здесь непрерывная, но не гладкая (производные не существуют в точке перегиба). Как вариант можно воспользоваться субградиентными методами, то есть, вычислять производную по правилу:

Но изначально решение задачи оптимизации метода опорных векторов сводился к решению системы (*). То есть задаче квадратичного программирования, минимизации коэффициентов ω при линейных ограничениях в виде неравенств. Такой подход приводит к достаточно эффективным численным методам и, кроме того, позволяет выделить объекты (наблюдения), на основе которых рассчитываются коэффициенты ω и b. Это интересная дополнительная информация о структуре обучающей выборки.

Я не буду приводить подробный вывод задачи квадратичного программирования для системы (*). Для тех, кто хочет погрузиться в эту математику, скажу лишь, что здесь используется условие Каруша-Куна-Таккера с поиском седловой точки функции Лагранжа. В итоге мы приходим к тому, что коэффициенты ω могут быть вычислены по формуле:

где  - некоторые коэффициенты, которые также вычисляются по ходу решения данной оптимизационной задачи. То есть, получается, что оптимальный вектор ω представляется в виде линейной комбинации наблюдений из обучающей выборки. И если для какого-либо i-го наблюдения , значит, он не используется для вычисления вектора ω. Что примечательно, нулевых значений λ получается достаточно много и из всей обучающей выборки остается несколько, которые и играю роль при расчете коэффициентов. Такие наблюдения (векторы) получили название опорных. 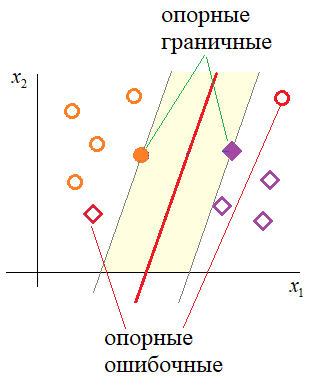Отсюда и пошло название метод опорных векторов.

Вообще, значения коэффициентов λ можно интерпретировать, следующим образом:

•  - периферийные (неинформативные) объекты;
•  - опорные граничные объекты;
•   - опорные ошибочные объекты.

Реализация SVM на Python

Давайте теперь посмотрим, как можно применить всю эту математику в конкретной практической задаче бинарной классификации. Я снова возьму ту же самую задачу линейно разделимых образов гусениц и божьих коровок:

И воспользуемся готовой реализацией метода опорных векторов из библиотеки Scikit-Learn:

from sklearn import svm

Готовую реализацию можно посмотреть в файле:

machine_learning_20_1_svm.py

После запуска программы увидим следующие значения коэффициентов вектора ω:

[ 0.24371833 -0.13071248  0.01218592]

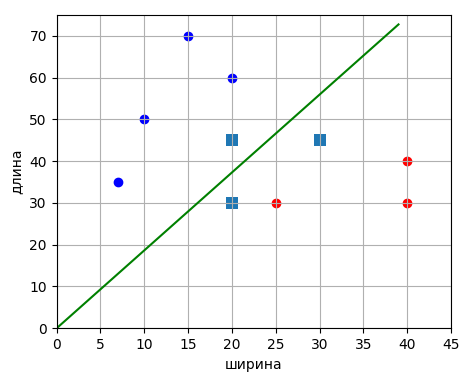
(здесь последний коэффициент – это смещение b). А также список опорных векторов, для которых :

[[20. 45.  1.]

 [20. 30.  1.]

 [30. 45.  1.]]

Визуализация этих данных дает нам следующую картину:

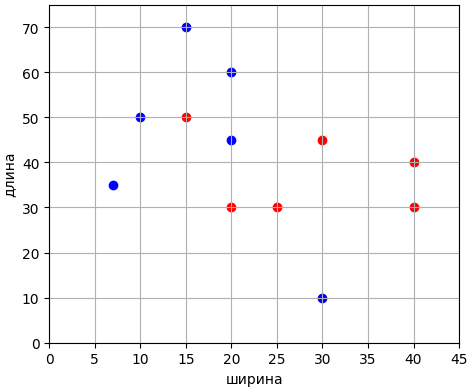
Как видим, разделяющая линия действительно проходит по центру полосы, образованной опорными векторами.

Давайте добавим в выборку два новых образа, которые будут являться выбросами и сделают выборку линейно неразделимой:

Получим следующее распределение наблюдений:

Реализуем SVM для такого случая. Здесь мы будем использовать только класс SVC, так как прежний LinearSVC применим только к линейно разделимой выборке. Программу можно посмотреть в файле:

machine_learning_20_2_svm.py

После запуска мы увидим качество классификации:

[-2  2  0  0  0  0  0  0  0  0  0  0]

(здесь нули соответствуют верной классификации, а не нулевые значения – ошибочной). Как видим, классификатор ошибся только на двух первых наблюдениях, в которые мы прописали выбросы, то есть, он корректно построил разделяющую гиперплоскость. Кроме того, видим список опорных векторов:

[[30. 10.  1.]

 [20. 60.  1.]

 [20. 45.  1.]

 [ 7. 35.  1.]

 [15. 50.  1.]

 [20. 30.  1.]

 [25. 30.  1.]

 [30. 45.  1.]]

и их стало заметно больше предыдущего случая (при линейно разделимой выборке).

Я надеюсь, что из последних двух занятий у вас сложилось представление о принципах работы метода опорных векторов и его реализации на Python с использованием пакета Scikit-Learn и линейным классификатором.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

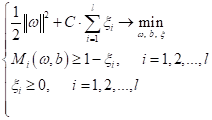Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation