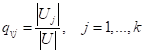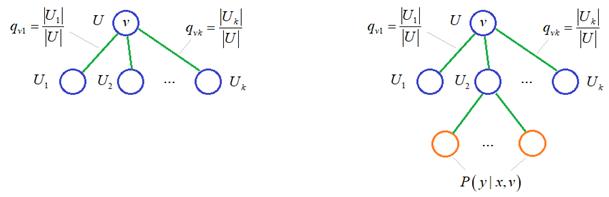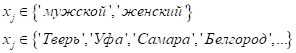Усечение (prunning) дерева, обработка пропусков и категориальных признаков

Практический курс по ML: https://stepik.org/course/209247/

На предыдущем занятии мы с вами рассмотрели алгоритм классификации ID3, который реализует жадную стратегию при построении решающих деревьев и использует энтропию для вычисления информативности (impurity) текущих вершин.

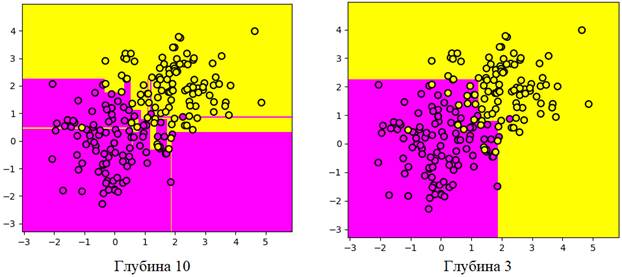
Однако, часто дерево в результате получается сильно переобученным, то есть, слишком хорошо подгоняется под данные обучающей выборки, что резко снижает качество прогнозирования на отложенной (тестовой) выборке. Разумным решением здесь кажется ограничить глубину решающего дерева и, таким образом, повысить его обобщающие способности.

Как я уже отмечал, процедура усечения дерева после его построения по обучающей выборке, называется pruning. В отличие от контроля глубины непосредственно при его построении. Этот процесс уже носит название pre-pruning или early stopping. Сейчас речь пойдет именно о pruning – усечения дерева после его обучения (построения).

Усечение дерева (pruning)

Так как мы имеем дело с переобучением (overfitting), то нам понадобится контрольная выборка. Именно на ней следует определять качество прогноза решающего дерева. Контрольная выборка, как правило, формируется из 30% объектов исходных размеченных данных, а 70% составляет, собственно, обучающая выборка. Далее, мы перебираем все внутренние вершины дерева:

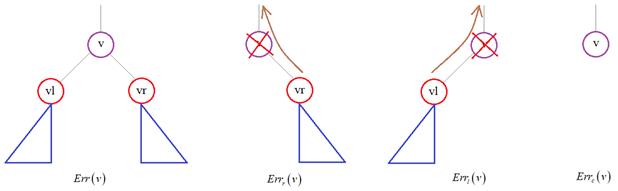
Опустим детали, в каком порядке это делается: вершины в одних алгоритмах перебираются снизу вверх, проходя все выше и выше до корня дерева, а в других, наоборот, от корня – до листовых.

Для каждой текущей внутренней вершины v мы определяем множество объектов  контрольной выборки, которые дошли до нее. Если оказывается, что это множество пустое (такое вполне может быть, т.к. используется отложенная выборка, а не обучающая, по которой строилось дерево), то данную вершину превращаем в листовую, так как высока вероятность, что поддерево этой вершины описывает какие то детали (возможно, выбросы) обучающей выборки и ее следует отбросить (обрезать). В листовую вершину прописываем метку класса, соответствующую наибольшему числу представителей объектов из обучающей выборки.

Если же множество объектов  не пустое, то вычисляем ошибки прогнозов для четырех возможных ситуаций усечения поддерева:

Выбираем вариант с наименьшей ошибкой, которая вычисляется по контрольной выборке. В результате, мы либо оставляем все как есть, либо усекаем правое или левое поддерево, либо превращаем вершину в листовую.

Вот в целом идея обрезки решающего дерева. И такая процедура рекомендуется, когда дерево строится в соответствии с жадным алгоритмом, т.к. высока вероятность, что оно окажется переобученным.

Обработка пропусков в данных

На данном этапе вы должны хорошо себе представлять идею построения решающих деревьев по жадному алгоритму и их усечение для повышения обобщающих способностей. Но один важный вопрос у нас остался в стороне. Как выполнять обработку реальных данных (входных векторов ), если у них отсутствуют нужные для вывода признаки?

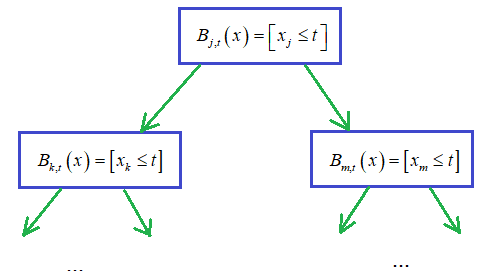
О чем здесь речь? Давайте представим, что у нас имеется следующий фрагмент решающего дерева. Чтобы обработать вектор  требуются признаки, которые, условно, я обозначил . Предположим, что объекты обучающей выборки имели эти признаки. Но в процессе эксплуатации или на этапе тестирования, выясняется, что некоторые объекты (редкие) не имеют этих признаков, то есть, возникают пропуски в данных. Такая ситуация не является чем то исключительным и встречается на практике. И требуется выработка некоторой стратегии (подхода) для обработки редких пропусков в данных.

Здесь существует несколько подходов решения этой задачи. Я приведу математический алгоритм, как приверженец строгой математики. Итак, у нас имеется обучающая выборка  по которой было построено решающее дерево. И пусть в некоторую вершину v попадает U объектов выборки . Также мы знаем, подмножества  объектов, которые перешли по каждой ветви вершины v в соответствии с заданным предикатом. Я здесь рассматриваю общую структуру решающего дерева с множеством потомков. Для бинарных деревьев достаточно положить k=2. На основе этих данных легко вычислить частотную вероятность того, что произвольный вектор  перейдет по одной из ветвей:

Если вершина v является листовой, то вероятность того, что вектор  принадлежит классу , можно определить по формуле:

То есть, мы в листовой вершине подсчитываем представителей класса  и делим на общее число объектов U, которые в нее попадают.

Зная вероятности:

 и

мы можем рекуррентно их пересчитывать для любой промежуточной вершины по формуле:

То есть, проходим по ветвям вершины v и суммируем вероятности листовых вершин . Если следующая вершина не листовая, то для нее применяется та же самая формула по рекурсии. В результате, мы получаем вероятность того, что некоторый вектор  принадлежит классу .

А дальше все просто. Если в какой-либо промежуточной вершине v для вектора  не существует нужного для предиката признака , то он относится к классу, у которого наибольшая вероятность:

На мой взгляд, это достаточно стройный и логичный алгоритм обработки пропущенных признаков для входных векторов .

Обработка категориальных признаков

До сих пор мы считали, что вектор  представлен числовыми признаками и потому, для них можно было определять предикаты вида:

Но не редко встречаются задачи, когда какой-либо признак (а может быть и несколько) относятся к категориальным, то есть, принимают одно из заданного множества значений. Например, это может быть пол человека, или город, в котором он живет, и т.п.:

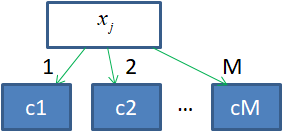
Как правильно их обрабатывать с помощью решающих деревьев? Давайте вначале обобщим запись для категориальных признаков, следующим образом:

Здесь C – это множество из M возможных категорий. И j-й признак вектора  принимает одно из M значений. Тогда, первое что приходит в голову, это определить вершину решающего дерева с M потомками для обработки такого признака:

Если мы теперь будем вычислять показатель качества разбиения для такой вершины так, как это делали для обычных числовых признаков, то получим выражение вида:

Напомню, что здесь

это impurity (информативность) вершины дерева. Так вот, выражение  при категориальных признаках коварно тем, что оно почти всегда будет выигрывать (принимать большее значение) в сравнении с числовыми признаками. Потому что информативность при большом количестве дочерних вершин будет быстро уменьшаться. Кроме того, такое разветвленное дерево образует гораздо более сложную иерархию взаимосвязей и, как следствие, очень быстро переобучается – подстраивается под обучающую выборку.

Существуют методики обхода этих проблем, например, через добавление регуляризационного множителя в формуле , но это часто приводит к другим дополнительным проблемам. Поэтому, здесь, лучше попытаться свести задачу обработки категориальных признаков к задаче бинарной классификации, когда вершина, по-прежнему, будет иметь только два потомка.

Опять же, в самом простом варианте, мы можем просто-напросто разбить все множество категорий на два непересекающихся множества:

А, затем, определить предикат, например, вида:

 или, наоборот,

То есть, здесь нам необходимо определить (подобрать) содержимое множеств  для формирования предиката . Если решать эту задачу «в лоб», то получим:

вариантов разбиений. Как вы понимаете, даже при небольшом числе M (от 10 и выше) мы получаем огромное количество вариантов. Выбрать из них лучшее простым перебором оказывается вычислительно очень сложно.

Вы можете сказать, а почему бы нам не воспринимать номера категорий, как числовой признак и не использовать его наряду с другими? И формировать предикат уже знакомого нам вида:

Это вполне разумная идея, только здесь есть один нюанс. Давайте представим, что наше решающее дерево связано с определением (прогнозом) уровня оплаты труда для некоторого индивида, представленного признаками входного вектора . И для j-го категориального признака имеем следующее соотношение между городами и уровнем оплаты:

Как видите, здесь уровень заработной платы то возрастает, то убывает с номером категории. Поэтому, увеличение порога t здесь не будет иметь прямую взаимосвязь с размером заработка. Например, если взять предикат:

то последняя 5-я категория не будет соответствовать максимальной оплате труда. А числовые признаки должны интерпретироваться именно так: чем больше номер категории, тем выше оплата труда.

По этому примеру, я думаю, вы уже догадались, что достаточно упорядочить категории по целевому значению и тогда их номера можно воспринимать как числовые признаки:

Вот общий принцип, положенный в основу обработки категориальных признаков как числовых. На практике, именно он чаще всего и используется.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation