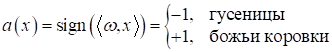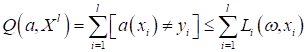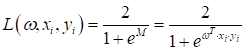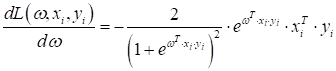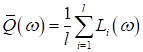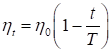Пример использования SGD при бинарной классификации образов

Практический курс по ML: https://stepik.org/course/209247/

На предыдущем занятии мы с вами познакомились с двумя подходами к реализации псевдоградиентных алгоритмов – это SGD и SAG. Чтобы в дальнейшем этот теоретический материал лучше воспринимался, на этом занятии я приведу пример использования SGD для все той же задачи бинарной классификации гусениц и божьих коровок.

Напомню, что у нас с вами имеется следующая обучающая выборка:

И нужно построить линейный классификатор:

который выдает -1 гусениц и +1 – для божьих коровок. То есть, целевые выходы .

Как всегда будем минимизировать эмпирический риск непрерывной функцией потерь:

В этот раз выберем сигмоидную функцию в качестве loss function:

Ее производная по , равна:

Таким образом, у нас есть все исходные данные для нахождения вектора параметров  с помощью алгоритма SGD. Напомню его псевдокод:

• Вход: выборка , шаг сходимости , скорость «забывания» .
• Выход: вектор весовых коэффициентов .

1) инициализация весов  некоторыми начальными значениями;

2) начальное вычисление функционала качества:

3) цикл

4)    случайный выбор наблюдения  из

5)    вычисление функции потерь

6)    шаг псевдоградиентного алгоритма:

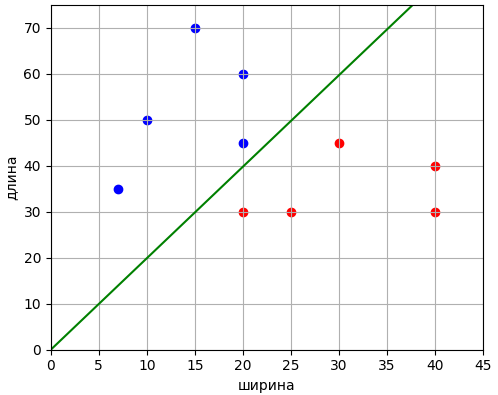
7)    пересчет функционала качества:

8) пока  и/или  не достигнут заданных значений

Реализуем теперь эти шаги на языке Python. Программу можно скачать по ссылке:

machine_learning_9_sgd.py

После запуска увидим следующие значения коэффициентов:

[ 0.32536188 -0.16612466  0.00541073]

и график разделяющей линии для двух классов:

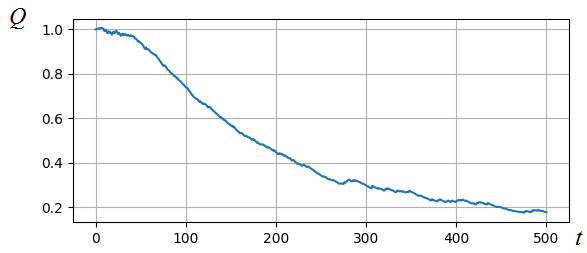
Как видите, мы смогли найти решение с помощью довольно простой реализации алгоритма стохастического градиентного спуска. Если дополнительно посмотреть на график показателя качества на разных итерациях, то видно, как он на протяжении всех 500 итераций постепенно уменьшается:

Конечно, это не самое лучшее решение и, очевидно, можно подобрать параметры так, чтобы сходимость была более быстрой. Например, уменьшать шаг по линейному закону:

или экспоненциальному:

Здесь T – параметр, определяющий скорость уменьшения шага обучения.

Некоторые другие рекомендации по выбору шага обучения можно посмотреть на занятии, посвященном градиентному алгоритму:

https://www.youtube.com/watch?v=OKeZEbJgQKc&list=PLA0M1Bcd0w8yZNgl5J814WQykTZnzj771&index=3

Я предлагаю вам в качестве практики поиграться гиперпараметрами этого алгоритма и попробовать найти лучшее решение.

Вообще, глядя на реализацию SGD, можно увидеть следующие его преимущества:

• малый объем вычислений;
• легко реализуется для самых разных функций потерь;
• можно использовать при потоковом обучении (когда наблюдения поступают непрерывно на вход алгоритма и обучающую выборку можно не сохранять в памяти);
• на очень больших выборках можно использовать только ее часть для обучения алгоритма;
• можно использовать в задачах с Big Data.

Ну а недостатки общие, присущие всем градиентным алгоритмам:

• застревание в локальных оптимумах;
• подбор гиперпараметров (шаг обучения, скорость «забывания», критерии останова и т.п.);
• может приводить к переобучению модели.

На последующих занятиях мы с вами посмотрим, как можно бороться с проблемами переобучения и застревания в локальных оптимумах градиентных алгоритмов.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation