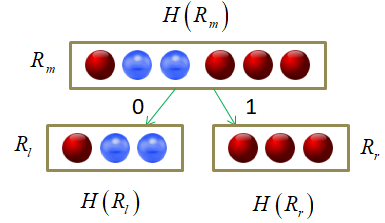
Построение решающих деревьев жадным алгоритмом ID3

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

На предыдущем занятии мы с вами познакомились с критериями выбора предикатов для разбиения множества данных в вершинах решающего дерева. В первую очередь – это impurity (информативность, мера неопределенности), обозначим ее через

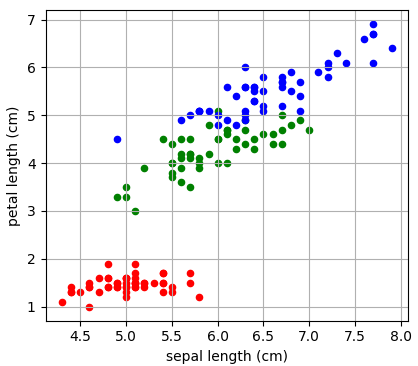
где - выборка, попавшая в текущую вершину. И показатель качества разбиения, который часто вычисляется как информационный выигрыш:

Давайте теперь воспользуемся этими показателями для построения бинарного решающего дерева. В качестве обучающей выборки возьмем 150 объектов трех классов ирисов (50 в каждом классе), распределенных в двумерном признаковом пространстве: длина и ширина лепестков:

То есть, входные векторы будут иметь два числовых признака:

Существует несколько распространенных алгоритмов построения решающих деревьев. Вначале я рассмотрю самый простой, который называется ID3 (Iterative Dichotomiser 3), разработанный Россом Куинланом в 1986 году для задачи классификации. Этот алгоритм использует энтропию в качестве информативности и реализует жадную стратегию, то есть, в каждом узле дерева, начиная с корневого, находит такой признак j и такой порог t, которые дают наибольшее значение показателя :

Затем, построение рекурсивно повторяется для каждой новой вершины.

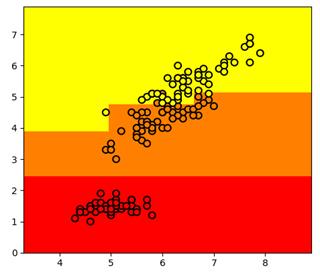
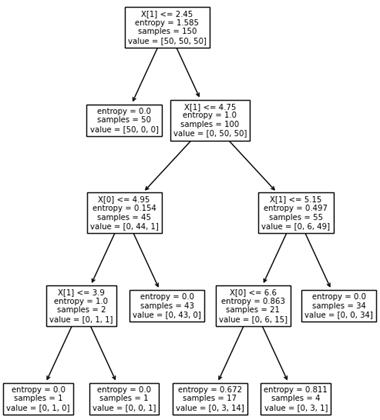
Вот пример разбиения обучающего множества деревом глубиной 4. Само дерево имеет вид:

Отсюда хорошо видно, как происходило разбиение. Вначале были отделены все красные объекты выборки по второму признаку (длина лепестка) с порогом t = 2,45 и предикатом:

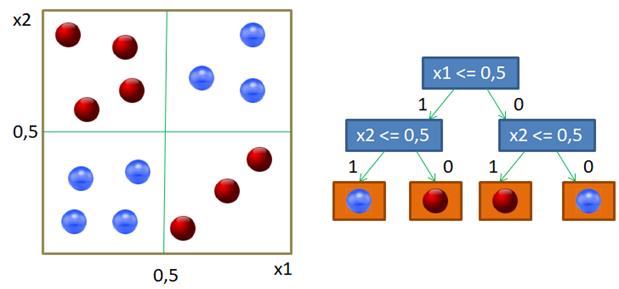
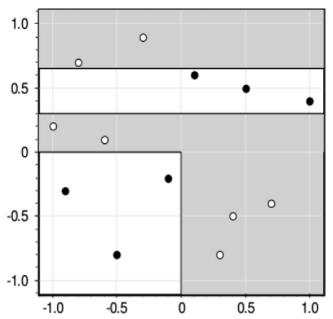
Если предикат выполняется, то попадаем в листовую вершину с нулевой энтропией и 50-ю представителями класса «красных» объектов. Во вторую вершину попадает 100 объектов двух других классов с энтропией, равной 1. Далее, мы делим объекты второй вершины дерева также по второму признаку и уровню 4,75. Формируются следующие две вершины. И так далее, пока либо не будет достигнута нулевая энтропия и сформирован лист дерева, либо глубина дерева достигнет уровня 4. (Этот максимальный уровень был задан при генерации данного решающего дерева.) В каждой листовой вершине мы сохраняем метку класса с наибольшим числом представителей.

Вот наглядный пример работы жадного алгоритма ID3. Казалось бы, все прекрасно и ничто не мешает нам использовать его в самых разных задачах. Однако, практика показала, что жадная стратегия построения деревьев часто не самая лучшая. Простой контрпример – задача XOR, когда объекты двух классов сосредоточены в разных углах квадрата:

Жадная стратегия дает, следующее решающее дерево:

Но, тем не менее, алгоритм ID3 относительно прост в реализации, а потому является основой для более сложных подходов к построению решающих деревьев, о которых мы поговорим на следующих занятиях.

Критерии останова (методы регуляризации)

Когда выполняется построение решающих деревьев по множеству данных (обучающей выборки), важно определить для алгоритма критерии формирования листовых вершин. Один из них очевиден. Когда impurity вершины равна 0, то в ней присутствуют представители только одного класса, а потому дальнейшее деление выполнять не нужно. Однако на практике применяют и другие критерии останова. К основным можно отнести, следующие:

impurity равна нулю или меньше некоторого заданного значения;
число объектов в вершине меньше заданной величины;
вероятность правильной классификации объекта больше заданной величины;
достигнуто максимальное количество листьев в дереве;
достигнута максимальная заданная глубина дерева.

Конечно, могут быть использованы и другие критерии, это лишь часто применяемые. Причем, в процессе построения дерева можно использовать сразу несколько критериев и, обычно, так и делают. Их выбирают из расчета получения хорошей обобщающей способности обученного (результирующего) дерева, то есть, критерии формирования листовых вершин можно рассматривать как эвристики регуляризации решающего дерева.

Применять критерии останова также можно по разному. Либо сразу в процессе построения дерева, при формировании каждой текущей вершины. Такой способ называется pre-pruning или early stopping. Либо, построить дерево по жадному алгоритму без сильных ограничений, а затем провести его стрижку (pruning), то есть, удалять отдельные вершины так, чтобы качество его работы оставалось примерно на том же уровне. Причем, качество такого дерева следует проверять по отложенной (тестовой) выборке (а не обучающей).

Преимущества и недостатки жадной стратегии

Итак, я думаю, в целом идея построения решающих деревьев по алгоритму ID3 вам понятна. В заключение отмечу преимущества и недостатки такого подхода.

Достоинства:

Интерпретируемость и простота классификации (легко объяснить результат классификации эксперту).
Допустимы разнотипные данные и пропуски в данных.
Не бывает отказов от классификации.

Недостатки:

Жадная стратегия в большинстве задач излишне усложняет структуру дерева, то есть, приводит к его переобучению.
Чем дальше от корня дерева, тем меньше объектов в листовых вершинах, а значит, ниже статистическая надежность различных показателей, например, вероятности появления того или иного класса.
Высокая чувствительность к шуму в объектах выборки и критерию информативности (impurity).

Некоторые из приведенных достоинств и недостатков присущи вообще всем решающим деревьям. Например, простота интерпретации результата, обработка пропусков данных (об этом речь пойдет дальше), высокая чувствительность к шумам (выбросам). Все это следствие самой структуры логических выводов с помощью решающих деревьев. На следующем занятии мы рассмотрим методику усечения (pruning) переобученных деревьев для повышения их обобщающих способностей.