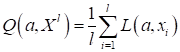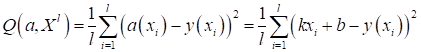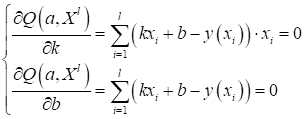Линейные модели. Градиентный алгоритм
Что такое машинное обучение? Обучающая выборка и признаковое пространство
Постановка задачи машинного обучения
Линейная модель. Понятие переобучения
Способы оценивания степени переобучения моделей
Уравнение гиперплоскости в задачах бинарной классификации
Решение простой задачи бинарной классификации
Функции потерь в задачах линейной бинарной классификации
Стохастический градиентный спуск SGD и алгоритм SAG
Пример использования SGD при бинарной классификации образов
Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam
L2-регуляризатор. Математическое обоснование и пример работы
L1-регуляризатор. Отличия между L1- и L2-регуляризаторами
Обучающие курсы
Python Python ООП Структуры данных Django C/C++
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наш канал

Главная
ML
Линейные модели. Градиентный алгоритм

Постановка задачи машинного обучения

Здравствуйте, дорогие друзья! Мы продолжаем курс по машинному обучению. На предыдущем занятии мы ввели понятие обучающей выборки 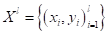и признакового пространства в виде матрицы 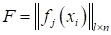. Будем полагать, что набор этих признаков и подается на вход алгоритмов. Причем, в частном случае, когда

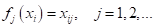
имеем неизменные исходные данные измерений .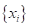

Получается, что идеальный алгоритм должен уметь отображать входы 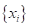в соответствующие выходы 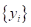. На уровне математики это можно записать через функциональную зависимость между входами и выходами:

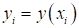
Причем, функциональная в широком смысле слова – это может быть любой алгоритм, связывающий вход с выходом. Но мы эту взаимосвязь не знаем. Целью обучения, как раз и является найти такую модель, решающую функцию (decision function), которая бы приближала ответы

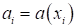
к требуемым 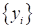на всем множестве возможных входных данных X (не только для обучающей выборки, но для всех возможных наблюдений той же природы). Это и есть общая постановка задачи машинного обучения.

Конечно, в таком виде совершенно непонятно, как ее решать, как искать правило преобразования 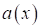? Необходима конкретизация. По сути, весь курс машинного обучения – это и есть различные вариации решения поставленной задачи.

Как можно ее решить? Наверное, одним из самых простых подходов (и наиболее часто используемых), представить функционал 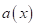в виде некоторой выбранной нами параметрической функции:

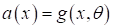
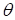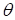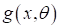с настраиваемым набором параметров . То есть, мы сводим задачу обучения к поиску неизвестных параметров и делаем это (в самом простом, но распространенном случае) по обучающей выборке. Причем вид самой функции может быть сколь угодно сложным (в математическом смысле) и в общем случае состоять из композиции других, более простых функций. То есть, вид функции 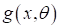должен отражать характер (природу, модель) изменения данных между входом и выходом, а параметры 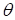подгоняют ее под конкретный набор данных.

Чтобы все это было понятнее, давайте рассмотрим классический пример такой задачи – линейную регрессию, когда входы и выходы имеют ярко выраженную функциональную зависимость вида:

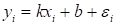
(здесь 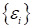- гауссовский (нормальный) шум с нулевым средним и некоторой небольшой дисперсией). Так как мы не можем прогнозировать случайные отклонения, то самое разумное описать модель данных в виде линейной функции с двумя неизвестными параметрами :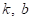

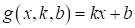
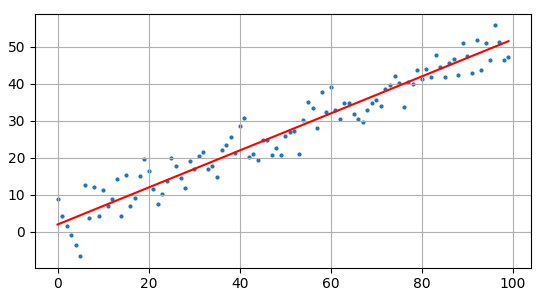
В результате, мы имеем вектор параметров , которые определяют конкретный наклон и сдвиг линейной функции. То есть, исходная функция 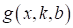описывает весь класс прямых, а при конкретных получаем определенную прямую для данных обучающей выборки.

Вот принцип параметрической оптимизации, который расширяется на произвольные функциональные зависимости выходов от входов.

Этап обучения

Хорошо, решающая функция 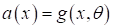в виде параметрической функции, определена. Как теперь нам найти значения параметров 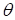на множестве входов и выходов 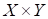обучающей выборки? Очевидно, они должны быть подобраны так, чтобы уменьшить ошибки между заданными выходами 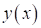и теми, которые получаются в нашей модели :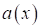

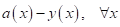
Но сама по себе ошибка в качестве оптимизируемой величины не очень удобна, т.к. в точке минимума (нуля) она не образует точки экстремума. Математически было бы лучше использовать функцию, которая бы возрастала с увеличением ошибки и убывала бы с ее уменьшением. Например, можно выбрать, следующие:

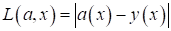- абсолютная ошибка;
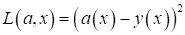- квадратичная ошибка.

Подобные функции получили название функций потерь 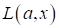(loss function), которые, фактически, вычисляет меру потерь (несоответствия) между нашей моделью и обучающей выборкой. Конечно, таких функций огромное количество и с некоторыми из них мы будем знакомиться по мере прохождения этого курса.

Однако, сама по себе функция потерь – это случайная величина, которая зависит от алгоритма 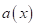и текущего входного вектора 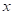. Поэтому оптимизировать одно какое-то конкретное значение функции потерь – неправильно. Нужно сделать так, чтобы на всем обучающем множестве, в среднем, ошибка была бы минимальна. В результате мы приходим к понятию среднего эмпирического риска:

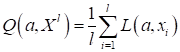
(Здесь 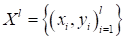- обучающее множество). Фактически, это и есть показатель качества, который нужно минимизировать, подбирая значения вектора параметров .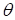

Например, если вернуться к нашей задаче линейной регрессии и в качестве функции потерь выбрать квадрат ошибки, то получим функционал качества в виде:

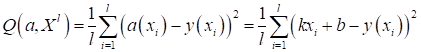
В данном случае параметры 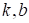легко вычисляются из решения следующей системы линейных уравнений:

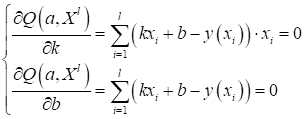
Это известная задача под названием метод наименьших квадратов (МНК) и я ее подробно рассматривал в одном из видео:

https://youtu.be/8sVfWyQrMiM

Если вы с ним не знакомы, то советую посмотреть этот материал.

Итак, резюмируя материал этого занятия, можно отметить следующие четыре пункта:

Общая задача машинного обучения ставится как поиск модели 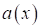, которая наилучшим образом описывает природу зависимости входных данных 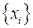и целевых выходных значений .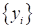
Задачу поиска наилучшей модели часто сводят к задаче параметрической оптимизации функции вида .
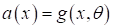Для нахождения подходящих параметров 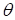вводится функция потерь 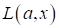и определяется средний эмпирический риск 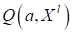. Минимизируя этот показатель качества, получаем набор параметров 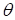по обучающей выборке.
На основе найденной зависимости 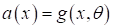в дальнейшем вычисляются выходные значения 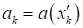при предъявлении нового входного вектора 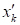той же природы, что и при обучении.

Эти четыре этапа представляют собой общий принцип, лежащий в основе всех алгоритмов машинного обучения.

Постановка задачи машинного обучения

Этап обучения

Видео по теме