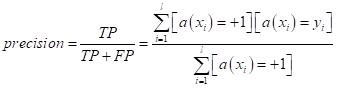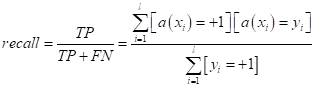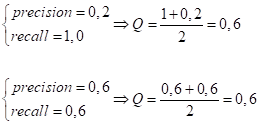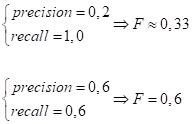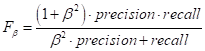SVM, PCA, показатели качества
Введение в метод опорных векторов (SVM)
Реализация метода опорных векторов (SVM)
Метод опорных векторов (SVM) с нелинейными ядрами
Вероятностная оценка качества моделей
Показатели precision и recall. F-мера
Метрики качества ранжирования. ROC-кривая
Метод главных компонент (Principal Component Analysis)
Сокращение размерности признакового пространства с помощью PCA
Сингулярное разложение и его связь с PCA
Многоклассовая классификация. Методы one-vs-all и all-vs-all
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
SVM, PCA, показатели качества

Показатели precision и recall. F-мера

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

На предыдущем занятии мы с вами увидели, как корректно оценивать уверенность модели отнесения объекта к одному из двух классов, используя значения вероятностей. Обычно, это вполне удовлетворительная характеристика, если классы в выборке сбалансированы, то есть, присутствует примерно одинаковое число объектов первого и второго классов. Однако, ситуация кардинально меняется, если мощности классов имеют сильную диспропорцию. Здесь часто приводят пример задачи кредитного скоринга, когда модель прогнозирует выдавать заемщику кредит или отказать. В этом случае может оказаться, что среди большого числа заявок, кредиты одобряются лишь небольшой части.

Давайте представим, что из 1000 заявок реально было одобрено только 100:

№	Заявка: з/п, стаж, возраст, долги	Одобрение
1	30000, 5, 35, 0	+1
2	23450, 10, 44, 0	+1
…	…	…
100	50000, 7, 54, 5000	+1
101	10000, 5, 60, 7000	-1
102	14500, 17, 55, 500	-1
…	…	…
1000	20000, 3, 65, 0	-1

В выборке налицо сильный дисбаланс классов: в первом всего 100 объектов, а во втором – 900. И если оценивать качество алгоритма, например, по метрике accuracy:

то при константной модели:

получим значение:

Если не знать о дисбалансе классов, то можно было бы подумать, что мы получили отличный результат, а в действительности прекратили функционирование кредитной организации, т.к. она всем желающим взять кредит выдает отказ.

Помимо дисбаланса классов (а, возможно, и совместно с ним), цена ошибки за неверный прогноз может отличаться для разных заемщиков. Например, если алгоритм отказал в кредите очень надежному заемщику, то разумно такой ответ штрафовать гораздо сильнее, чем при отказе сомнительному заемщику. Этот момент метрика accuracy также не учитывает.

Чтобы точнее оценивать качество модели в таких ситуациях, вводят следующие понятия:

	Ответ классификатора	Правильный ответ
TP, True Positive
TN, True Negative
FP, False Positive
FN, False Negative

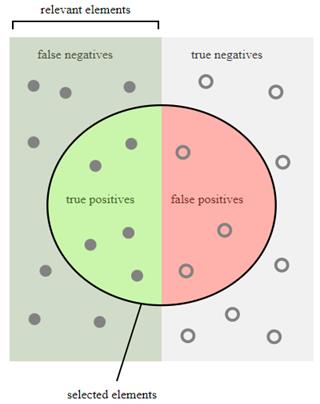
Запомнить это можно очень легко. Второе слово (positive или negative) относится к выходу классификатора, а первое (true или false) – верен ли выход классификатора или нет.

Еще все эти комбинации при бинарной классификации представляют в виде такой таблицы:


	TP	FP
	FN	TN

Что вам проще, первый или второй вариант, выбирайте сами.

Итак, на основе прошлых эмпирических данных (это может быть и сама обучающая выборка), мы легко можем вычислить величины TP, FP, FN, TN – это соответствующие числа верных и неверных прогнозов алгоритма для обоих классов.

Например, мы оцениваем работу спам-фильтра какого-либо мессенджера и получили следующие данные:

(класс +1): пришло 100 нормальных (не спам) сообщений, из которых модель 90 пометила как не спам, а 10 – как спам;
(класс -1): пришло 10 спам-сообщений, из которых модель выделила только 7.

Получаем значения величин:

TP = 90; FN = 10; FP = 3, TN = 7

Условное распределение величин TP, FP, FN, TN можно представить графически в виде, следующей диаграммы, взятой с сайта Wikipedia:

https://en.wikipedia.org/wiki/Sensitivity_and_specificity

Precision и recall

На основе этих данных мы легко можем вычислить уже знакомую нам метрику accuracy, следующим образом:

То есть, используя величины TP, FP, FN, TN мы можем строить самые разные метрики. Давайте попробуем сконструировать новые показатели алгоритма, которые бы учитывали дисбаланс классов. Первой такой величиной будет precision (точность):

Она показывает, насколько можно доверять модели, когда она выдает положительный класс +1. Например, применительно к задаче кредитного скоринга, в знаменателе указаны все заемщики, которым модель выдала кредит, а в числителе – те из них, которые вернули кредит. Если оказывается, что эта величина 0,9 и более, то очевидно, что к рекомендациям такой модели следует прислушаться, т.к. подавляющее большинство рекомендаций оправдывается (заемщики возвращают кредит).

Но этой характеристики явно недостаточно, т.к. она не показывает насколько анализируемая модель охватывает всех заемщиков положительного класса. Возможно, она так завышает требования и выдает кредиты только очень состоятельным организациям или гражданам. Тогда, как менее состоятельные клиенты ею не учитываются, а среди них, очевидно, не мало тех, кто способен расплатиться по взятым обязательствам. Поэтому вторая характеристика должна показывать охват положительного класса нашей моделью. Она называется recall (полнота) и определяется выражением:

Объединение precision и recall

В идеале хорошая модель должна показывать высокие значения по обоим параметрам precision и recall. Однако, на практике отдают большее предпочтение одному показателю и меньшее – другому, так как одновременно максимизировать оба (найти такую модель) часто очень сложно. И здесь возникает следующая задача – объединения этих двух характеристик в одну, чтобы на выходе мы имели одно число, по которому можно было бы судить о качестве полученной модели.

Линейная комбинация (не рабочий вариант)

Первое, что приходит в голову, просто взять линейную комбинацию от этих признаков с некоторыми весами:

Но это не очень хороший вариант, т.к. для любых можно придумать контрпример, где показатель Q даст спорный результат. Например, при , получим:

и, далее:

Как видите, при двух совершенно разных показателях precision и recall, мы получаем одно и то же значение Q. Значит, такое объединение не дает объективной картины.

Использование функции min

Другой радикальный вариант – это воспользоваться функцией min, для выбора минимального значения из двух показателей:

Но здесь, очевидно, возникает другой недостаток, мы в значении Q будем видеть только одну минимальную величину, а вторую просто отбрасывать. Это не очень хорошо, так как, обычно, важны обе характеристики с разными весами.

Гармоническое среднее (F-мера)

Приемлемый результат можно получить с помощью вычисления гармонического среднего (F-меры) на основе precision и recall:

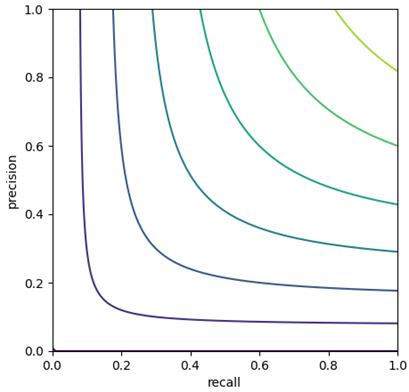
Почему это хорошо, я покажу на линиях уровня. Пусть у нас есть график на плоскости. По одной оси откладываем различные значения precision, а по второй – recall:

Мы видим скругленные линии. Это значит, что для любого фиксированного значения F, увеличивая, например, precision, будет уменьшаться recall. Или, увеличивая recall, будет уменьшаться precision. При этом, гармоническое среднее напоминает линии уровня функции min, то есть, как бы «тянется» к меньшей величине. Например:

Fβ-мера

Рассмотренная F-мера уже дает неплохие результаты объединения двух показателей precision и recall, но она учитывает их в равной степени. А, что если мы хотим уделять больше внимания показателю precision или, наоборот, recall? Для этого было придумано расширение F-меры до Fβ-меры, которая определяется выражением:

Здесь β – любое действительное число:

При β=1 получаем обычную F-меру.

Геометрическое среднее

Несколько реже используется геометрическое среднее двух показателей:

Эта метрика считается хуже, чем F-мера, т.к. «тяготеет» к более высоким значениям. Например:

То есть, гармоническое среднее (F-мера) оказывается более требовательной к обеим метрикам precision и recall, а геометрическое среднее в большей степени «перекошено» к более высоким значениям. Поэтому, на практике чаще выбирают именно F-меру и ее аналоги.