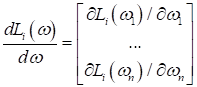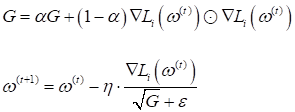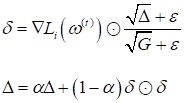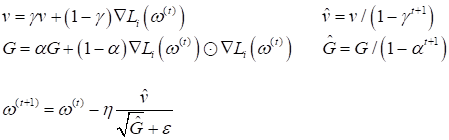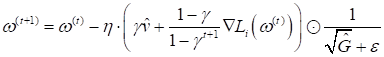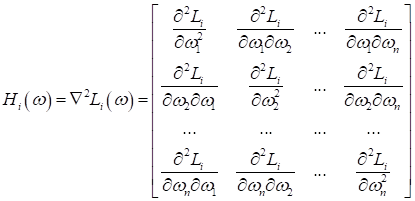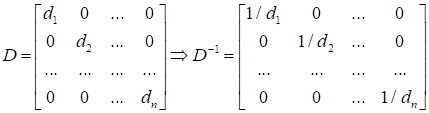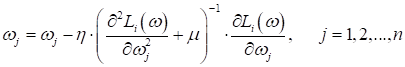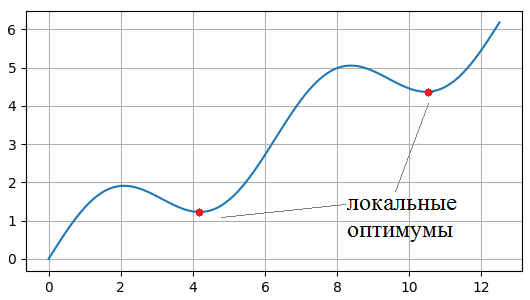
|
Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, NadamПрактический курс по ML: https://stepik.org/course/209247/ На данный момент мы с вами познакомились с численными методами оптимизации функций – градиентными алгоритмами. Но, как я отмечал, они имеют один существенный недостаток – застревание в локальных оптимумах.
Очевидно, в таких точках производная равна нулю, а значит, дальнейшее изменение весов по правилу:
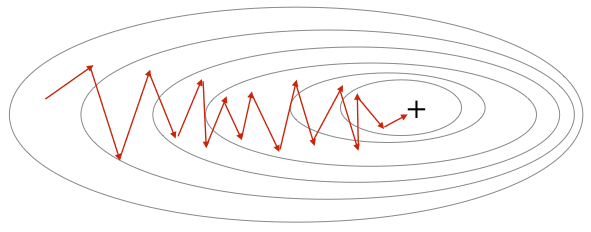
происходить не будет. Кроме того, стохастические градиентные алгоритмы могут образовывать сильные колебания (флуктуации) при движении к точке минимума функции:
Метод импульсов (momentum)Для некоторого исправления этих недостатков было придумано множество эвристик. Одна из первых была предложена Борисом Теодоровичем Поляком в 1964 году. Он предложил усреднять градиент по шагам с помощью экспоненциального скользящего среднего:
или, переобозначая:
метод импульсов часто записывают в виде:
(Мы с вами уже
знаем, что означает экспоненциальное скользящее среднее по примерно последним
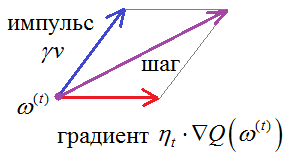
Что мы в итоге получаем? Во-первых, сглаживание градиента и уменьшение амплитуд его случайных изменений. Во-вторых, при попадании в небольшой локальный минимум, градиент не станет мгновенно равным нулю, мы, как бы, по инерции продолжим движении в прежнем направлении. И если оптимум (ямка функции) был неглубоким, то перескочим его и продолжим поиск, в надежде найти меньшее значение функции. Практика показала, что такая эвристика действительно улучшает сходимость стохастических градиентов и позволяет с большей вероятностью находить по настоящему глубокие минимумы функции. Стохастический градиент с импульсом Нестерова (NAG – Nesterov’s accelerated gradient)Давайте еще раз посмотрим на формулу вычисления импульса (усредненного значения) градиента:
Здесь,
фактически, выполняется сложение двух векторов: v и
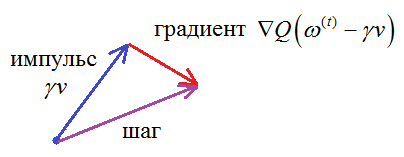
Но на момент
вычисления градиента мы уже знаем, что сместимся на величину
И такой подход, как правило, показывает лучшую сходимость к точке оптимума. Алгоритм был предложен Нестеровым в 1983 году и активно применяется (наряду с другими оптимизаторами) при обучении алгоритмов, в частности, нейронных сетей. RMSProp (running mean square)Метод импульсов с поправкой Нестерова – это достаточно очевидные эвристики. В последующем были предложены более сложные и изощренные подходы. Например, довольно часто при обучении нейронных сетей используют оптимизатор RMSProp. Его целью является не только сглаживание псевдоградиента в стохастических алгоритмах, но и нормализация скорости изменения вектора весов:
О чем здесь речь? Часто в задачах многомерной оптимизации, когда число подбираемых весовых коэффициентов не 2-3, а десятки, сотни, тысячи и более, частные производные по функции потерь от каждого из них могут сильно различаться:
А это, в свою очередь, приводит к сильному изменению одних весовых коэффициентов и практически оставляет без изменения – другие:
Так вот, чтобы
нормализовать скорость адаптации весов вектора
(здесь деление
векторов во второй формуле выполняется поэлементно). Вначале мы похожим образом
вычисляем экспоненциальное скользящее среднее, но не по градиентам, а по
квадратам градиентов (здесь AdaDelta (adaptive learning rate)Как развитие
этой идеи выступает еще одна эвристика – алгоритм AdaDelta. Ее цель не
только выравнивать скорость сходимости по компонентам настраиваемых параметров Начало алгоритма абсолютно такое же, как и в RMSProp, мы вычисляем экспоненциальное среднее по квадратам компонентов вектора градиентов:
Но, затем,
вычисляем еще один вектор
То есть,
Причем,
гиперпараметр В ряде случаев такая эвристика действительно позволяет уйти от определения шага сходимости в градиентных алгоритмах. Adam (adaptive momentum)Следующая очень популярная эвристика, часто используемая для оптимизации стохастических градиентных алгоритмов, - это адаптивный импульс (Adam). Он был получен путем объединения метода импульсов и RMSProp. В результате, получился следующий алгоритм:
Здесь Любители строгой математики сейчас могут в недоумении смотреть на все эти формулы и задаваться вопросом, откуда вообще все это взялось? Из каких соображений? На самом деле, смотреть на все это следует лишь как на математическую формализацию некой идеи, которая пришла в голову их создателям. Конечно, каждая разумная идея содержит некую гипотезу об ускорении градиентных алгоритмов. Но доказательство ее справедливости часто сводится к экспериментам. Если метод действительно в ряде задач показывает хорошую эффективность, его оставляют и начинают применять. В противном случае – забывают. Поэтому приведенные формулы служат лишь для общего понимания идей, заложенных в тот или иной оптимизатор, чтобы вы понимали принцип его работы. Это главная цель данного занятия. Когда вам придется применять их на практике, то все приведенные здесь алгоритмы уже реализованы в стандартных пакетах, таких как: Scikit-Learn, Keras, Pytorch, Tensorflow и др. Ну а если понадобится погрузиться глубоко в математику некоторых оптимизаторов, то они подробно описаны в большом числе публикаций. Nadam (Nesterov-accelerated adaptive momentum)Естественное
развитие оптимизатора Adam – это добавление момента Нестерова при
вычислении градиентов. В результате получаем все те же самые формулы для
Вообще, самых разных оптимизаторов существует огромное количество. Уверен, каждый из вас при определенной тренировке сможет придумать и свой какой-нибудь. Поэтому, это все и называется эвристиками. Здесь нет строгой математики, которая бы давала один лучший, оптимальный результат и мы бы им только и пользовались. Этого на данном поле добиться пока не удается, хотя если посмотреть в сторону алгоритмов второго порядка, то можно нащупать некое более фундаментальное основание. Диагональный метод Левенберга-МарквардтаНапример, если записать метод Ньютона для нашей задачи многомерной оптимизации, то получим выражение вида:
Здесь
Если вычислить саму матрицу еще как-то можно, то на каждом шаге брать обратную матрицу в признаковом пространстве n, когда n = 100 000 и более, вычислительно очень затратно, а при размерностях 1 000 000 и выше – практически невозможно даже на современных компьютерах. Поэтому была предложена очередная эвристика (хитрость) – считать матрицу Гессе диагональной, то есть, обнулить все смешанные частные производные. Тогда для ее вычисления будет достаточно взять n вторых частных производных (по главной диагонали) и еще n операций деления при вычислении обратной матрицы, так как:
Обращать диагональные матрицы не составляет больших проблем. Именно это и предложили Левенберг и Марквардт – считать гессиан диагональной матрицей. Тогда алгоритм оптимизации можно записать в виде:
Здесь Какой оптимизатор выбратьНа этом я завершу обзор популярных оптимизаторов. Как я уже говорил, их огромное количество, но на практике используют лишь небольшую их часть. И здесь, естественно, возникает вопрос, как выбрать оптимизатор при решении конкретной задачи. Строгого математического ответа на этот вопрос не существует. Скорее, ориентируются на опыт и удачу. Просто перебирают несколько оптимизатор, исходя из знаний их работы и здравого смысла, а затем, оставляют один-два, которые предположительно сработали лучше всего. Далее, уже с их помощью пытаются улучшить показатели (найти глубокий минимум показателя качества) и при этом постараться не переобучить модель. Если вы предполагаете использовать оптимизаторы для обучения нейронных сетей, то под видео будут ссылки на занятия, где я показываю, как их можно применять в пакетах Keras и Tensorflow: Tensorflow – строим градиентные алгоритмы оптимизации: https://www.youtube.com/watch?v=WYme8F384as&list=PLA0M1Bcd0w8ynD1umfubKq1OBYRXhXkmH Keras – обучение сети распознаванию рукописных цифр: https://www.youtube.com/watch?v=oCXh_GFMmOE&list=PLA0M1Bcd0w8yv0XGiF1wjerjSZVSrYbjh Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
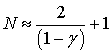отсчетам).
Затем, полученное значение v, используют для корректировки весов:
.
Графически, это можно представить, так:
.
Поэтому было бы правильнее вычислять градиент не в точке 
,
а в точке:
,
Джефри Хинтон на своем курсе по Deep Learning (глубокое
обучение) предложил делать следующую перенормировку шага обучения:
-
поэлементное умножение соответствующих компонент векторов). А, затем, нормируем
текущий вектор градиента на корень квадратный из усредненных (по экспоненте)
квадратов градиентов на последних итерациях. (Здесь 
-
небольшая константа для исключения деления на ноль). В результате, каждый
компонент вектора градиента 
будет
поделен на пропорциональное значение из вектора 
и,
таким образом, несколько нормирован. Благодаря этому выравнивается скорость
изменения коэффициентов в векторе 
,
чтобы нам не пришлось задумываться о способе выбора этого гиперпараметра.
для
нормировки, следующим образом:
(можно
просто положить равным 1).
-
номер итерации; 
-
нормированные векторы 
(нормировка
увеличивает 
.
,
а корректировка весов принимает вид:
- матрица Гессе
(гессиан), размерностью n x n:
-
это значение, которое предотвращает деление на ноль и кроме того, задает
скорость сходимости алгоритма, когда вторая производная обнуляется. Это
происходит в случаях линейного изменения функции потерь (ускорение равно нулю).
Здесь мы, фактически, следует только за градиентом, не обращая внимание на
вторые производные.
