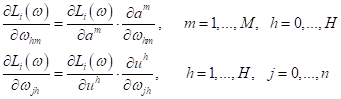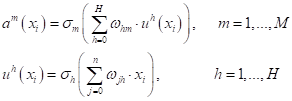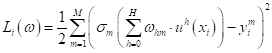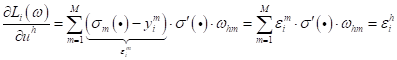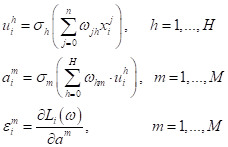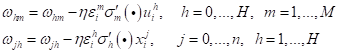Обучение нейронной сети. Алгоритм back propagation

Практический курс по ML: https://stepik.org/course/209247/

На предыдущем занятии мы с вами в целом познакомились с идеей полносвязных нейронных сетей (НС) и рассмотрели несколько простейших примеров. И здесь самой главной и сложной задачей является обучение таких структур. Я напомню, что нейронные сети относятся к параметрическим алгоритмам:

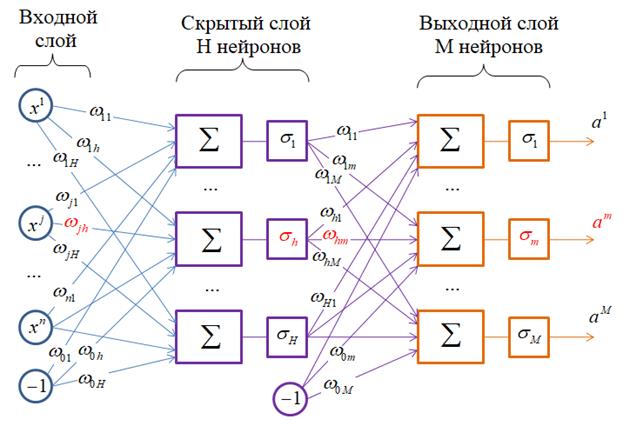
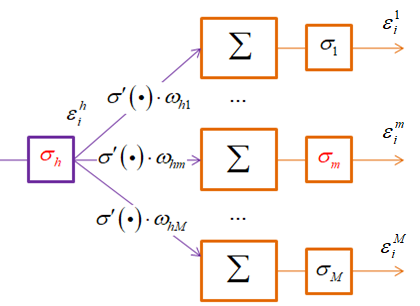
где  - набор (вектор или матрица) весовых коэффициентов.

Давайте, для определенности, возьмем структуру двухслойной НС:

Здесь весовые коэффициенты – это веса связей . Именно они настраиваются в процессе обучения НС так, чтобы каждому входному образу  из обучающей выборки  соответствовало целевое значение (или вектор) . Все остальные параметры (число нейронов в слоях, функции активации) задаются до обучения и не меняются. Получаем классическую оптимизационную задачу, которую мы много раз рассматривали на предыдущих занятиях. Для ее решения нужно выбрать функцию потерь:

и минимизировать функционал качества (эмпирический риск):

В общем случае задачу минимизации можно решить численно с помощью градиентного алгоритма. Учитывая, что обучающие выборки для НС, как правило, очень большие, то применяют стохастический градиентный алгоритм:

Вход: обучающая выборка ; шаг обучения ; параметр

Выход: вектор весовых коэффициентов

1: инициализировать веса  и по ним вычислить функционал

2: повторять

3:      выбрать случайный образ  из обучающей выборки

4:      вычислить значение функции потерь:

5:      корректировка весов:

6:      пересчет значения функционала:

7: пока значение  и/или веса  не стабилизируются.

Но оказывается такой классический подход, который мы применяли к линейным алгоритмам с небольшим числом параметров вектора  (до 1000), далеко не всегда можно применить к нейронным сетям. Почему? Все дело в вычислении градиента функции потерь, когда вектор параметров  содержит огромное количество N весов связей (от сотен тысяч и более). В этом случае вычислительная сложность градиента функции потерь на каждой итерации составит . И это очень много. Поэтому был придуман специальный алгоритм применительно к НС, который позволяет вычислить этот же самый градиент за линейное число операций, примерно:

где K – число слоев НС. Алгоритм получил название back propagation (обратное распространение ошибки).

В плейлистах по НС я приводил принцип его работы без математического вывода. Поэтому здесь восполню этот пробел и приведу математический вывод этого алгоритма применительно к полносвязной двухслойной НС прямого распространения. Но этот результат, затем, легко обобщается на НС с произвольным числом слоев.

Вывод алгоритма back propagation

Вывод алгоритма back propagation я взял из курса лекций профессора Воронцова, как наиболее простой из всего, что я видел:

https://www.youtube.com/watch?v=zbdgUZAzfQg

Наша цель научиться корректировать веса  у выходного слоя и веса  у скрытого слоя. Это значит, нам нужно научиться вычислять частные производные вида:

Для дальнейших выкладок нам нужно определиться с видом функции потерь. Для простоты возьмем квадратическую функцию (но те же самые выкладки можно повторить с любой другой дифференцируемой функцией потерь):

где

Теперь мы можем записать конкретное выражение для частной производной:

А перед вычислением другой частной производной  я перепишу выражение функции потерь в виде:

Отсюда мы явно видим зависимость функции потерь от . Соответственно, ее частная производная по , равна:

Эта последняя формула показывает, как вычисляется величина , которую мы условно назовем ошибкой на выходе i-го нейрона скрытого слоя. Фактически, мы вычисляем взвешенную сумму ошибок  на выходных нейронах, двигаясь по сети в обратном направлении:

По аналогии мы можем вычислять такие ошибки для любых промежуточных слоев в многослойных НС.

Теперь у нас есть все, чтобы вычислить итоговые градиенты функции потерь по весам НС:

и

Все, мы знаем как вычисляются частные производные по всем весам связей НС и можем их корректировать с помощью градиентного алгоритма.

Псевдокод алгоритма back propagation для нашей двухслойной НС можно записать следующим образом:

Вход: обучающая выборка ; шаг обучения ; параметр

Выход: вектор весовых коэффициентов

1: инициализировать веса  и по ним вычислить функционал

2: повторять

3:     выбрать объект  из обучающей выборки (например, случайно)

4:     прямой ход:

5:     пересчитываем функционал качества:

6:     обратный ход:

7:     градиентный шаг:

8: пока  не стабилизируется

Преимущества и недостатки алгоритма back propagation

Итак, благодаря алгоритму back propagation мы получаем следующие преимущества:

• быстрое вычисление градиента;
• возможность использования любых функций активаций, потерь (дифференцируемых) и применять для любого числа слоев;
• возможность динамического (потокового) обучения;
• сублинейное обучение на сверхбольших выборках (когда для обучения используется ограниченная подвыборка);
• возможность распараллеливания.

К недостаткам этого подхода можно отнести:

• медленная сходимость к точке минимума;
• застревание в локальных экстремумах;
• практически остановка обучения при наличии горизонтальных асимптот у функций активации ;
• проблема переобучения.

Но все эти проблемы, в общем то, вытекают из самого градиентного алгоритма и присущи всем оптимизационным подходам такого типа. Нейросети здесь не исключение. Но эти недостатки относительно успешно преодолеваются различными эвристиками. В частности, против застревания в локальных оптиумах используют оптимизаторы, о которых мы подробно говорили вначале этого курса. Проблема переобучения преодолевается с помощью метода Dropout, о котором я подробно рассказываю в плейлите по НС. А ускорение обучения в глубоких НС достигается за счет применения идеи статистической нормализации по мини-батчам – Batch Normalization. Обо всем этом и многих других моментах, связанных с проектированием и обучением нейронных сетей различных структур, смотрите в плейлистах по нейронным сетям на этом канале.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation