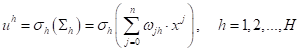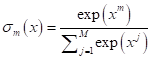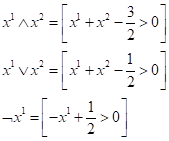|
Нейронные сети. Краткое введение в теориюНаверное, многие, кто начинает изучать машинное обучение, в первую очередь думают о нейронных сетях. Сейчас эта тема на вершине популярности благодаря новым техникам построения и обучения глубоких нейронных сетей (deep learning). Именно эти сети позволяют лучше многих других алгоритмов обрабатывать данные сложной структуры, в первую очередь изображения, звук, текст. А появление генеративно состязательных сетей в 2015 году дало возможность генерировать новые сложные структуры данных, такие как изображения, видео, звуки. В результате появились алгоритмы сочиняющие стихи, музыку. Программы по анимированию изображений, создания deep fake (дип фейков), раскраски и улучшения качества черно-белых лент старых фильмов, стилизации изображений и так далее. Сейчас глубокие нейронные сети применяются практически во всех сферах, где требуется обработка данных сложной структуры. Но почему они оказались так успешны на этом поприще? Ответ, в целом, очень прост. Глубокие нейронные сети в первых слоях формируют новые качественные признаки, которые гораздо проще обрабатывать стандартными алгоритмами, например, линейным классификатором в задачах распознавания. Однако, чтобы сеть представляла собой единое целое, то и выделение вторичных признаков и задачи их обработки объединяются в одну общую структуру под названием глубокие нейронные сети. Благодаря единой, целостной конструкции алгоритма в процессе их обучения происходит автоматическая настройка первых слоев, где формируются новые качественные признаки, и последних слоев, которые отвечают за обработку этих новых признаков. Получается тесная интеграция двух блоков общей схемы. И это, в итоге, заметно повышает качество работы сети в целом. По нейронным сетям я уже создавал довольно подробные курсы. Вот ссылки на эти плейлисты:
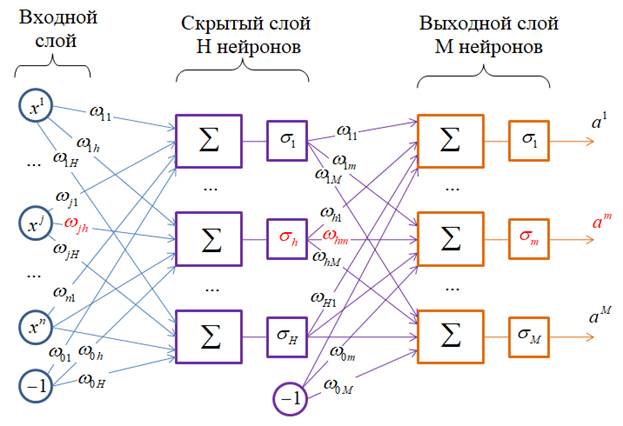
Поэтому не буду повторяться и пытаться уместить весь этот материал в курсе по машинному обучению. Нейронные сети – это одна большая и, в некотором смысле, отдельная область машинного обучения. Хотя, для их понимания нужно хорошо себе представлять и тот материал, что мы уже проходили. Но некоторые моменты, о которых мало или смазанно упоминал в тех плейлистах, я расскажу в рамках этого курса. Чтобы мы понимали друг друга, еще раз (в который раз) приведу общую схему полносвязной нейронной сети (НС) прямого распространения:
Здесь на вход подается вектор из n+1 признаков:
Затем, на каждом сумматоре вычисляется взвешенная сумма признаков с некоторыми весовыми коэффициентами:
Эта сумма пропускается через нелинейную функцию (функцию активации) и формируется выходное значение соответствующего нейрона скрытого слоя:
Получаем вектор промежуточных значений:
После этого
выходы
Вот в двух словах принцип работы полносвязной НС прямого распространения. Легко видеть, что каждый нейрон здесь представляет линейный алгоритм, подобно линейному классификатору:
То есть,
нейронная сеть – это суперпозиция линейных алгоритмов, но с нелинейными
функциями активаций. Почему так важно, чтобы функция
то мы получим суперпозицию обычных линейных алгоритмов, которые вырождаются в один линейный алгоритм. То есть, НС с линейными функциями активаций можно представить одним нейроном, в виде модели:
Чтобы суперпозиция имела смысл, должны использоваться нелинейные функции активации. Исключение составляют выходные нейроны, там иногда (в задачах регрессии) используются линейные активационные функции. Вообще, существует
определенный (джентельменский) набор для функций
И в выходных нейронах:
Конечно, существует и множество других функций активаций. Подробно о некоторых из них я рассказываю в курсе по нейронным сетям. Теорема о структуре полносвязных нейронных сетей прямого распространенияИтак, НС в каждом новом слое формирует новые признаки, которые подаются на модели (нейроны) следующего слоя. Тогда получается, что от слоя к слою могут формироваться все более и более сложные признаки и это, наверное, должно улучшать работу сети в целом? И здесь возникает вопрос, а сколько слоев нам следует взять, чтобы успешно решить поставленную задачу? Удивительно, но на этот вопрос есть строгий математический ответ. В 1989 году американский математик Джордж Цыбенко (George Cybenko) доказал, что при сигмоидной функции активации:
всегда можно подобрать такое конечное число нейронов H скрытого слоя, чтобы нейронная сеть:
аппроксимировала
произвольную непрерывную функцию
Из этой теоремы
вытекает, что двухслойная НС способна решить все те же задачи, что и
многослойная НС. По крайней мере, она может аппроксимировать любые непрерывные
функции Спрашивается, почему природа (эволюция) сформировала глубокие нейронные сети, хотя математика утверждает, что двух слоев достаточно? Здесь есть, по крайней мере, одна веская причина для перехода к многослойным сетям – общее число нейронов и скорость обучения. Приведенная теорема ничего не говорит о количестве нейронов H скрытого слоя. В общем случае эта величина может стремиться к очень большим значениям. И было экспериментально замечено, что многослойная сеть с меньшим числом нейронов способна аппроксимировать функцию с той же точностью, что и двухслойная. Мало того, формируя множество последовательных слоев, их структура может меняться от слоя к слою. Например, сверточные НС в первых слоях реализуют, так называемые, свертки, а в последних – идет обычная полносвязная сеть (в задачах классификации). Это позволяет естественным образом разделить функционал сети на выделение более содержательных вторичных признаков в первых слоях, и непосредственно классификацию – в последних полносвязных слоях. Двухслойные сети прямого распространения не обладают таким свойством. Также, несмотря на эту теорему, обучить на практике двухслойную НС, например, для решения задач классификации изображений, так, чтобы она решала задачу не хуже глубокой НС – не удается. Глубокие сети не только содержат меньше нейронов, но и проще обучаются на сложных задачах, таких как обработка изображений, звуков, текстов и прочее. Именно поэтому глубокие НС завоевали большую популярность и в ряде важных направлений остаются вне конкуренции. Нейронная реализация логических функцийВ заключение этого занятия продемонстрирую простые примеры нейронных сетей для решения задач классификации двумерных бинарных сигналов, то есть, входов вида:
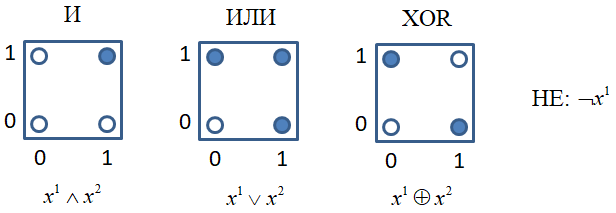
На уровне этих
бинарных признаков
А теперь поставим задачу классификации этих образов (закрашенные точки – класс 1, не закрашенные – класс 0) с помощью НС. Для трех функций И, ИЛИ, НЕ это делается очень просто. Можно заметить, что:
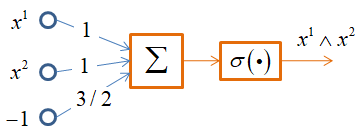
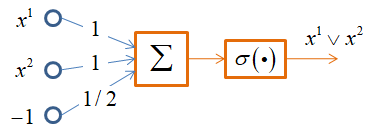
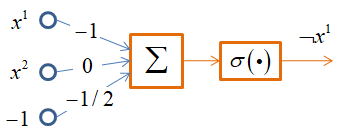
Здесь квадратные скобки – это нотация Айверсона. Как видите, мы расписали конъюнкцию, дизъюнкцию и отрицание через простые арифметические операции. Эти операции легко реализовать с помощью одного нейрона и пороговой функции активации:
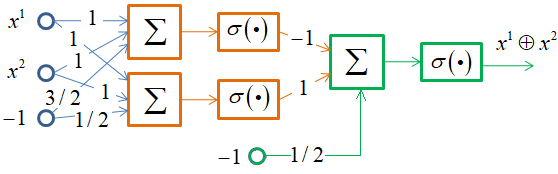
Однако, функцию XOR одним нейроном не описать. Но можно двухслойной НС по следующей схеме:
Здесь используются операции конъюнкции и дизъюнкции для формирования выходного значения. Получаем, следующую структуру НС:
В результате, мы смогли описать все базовые функции алгебры логики, а значит, с помощью комбинации таких сетей можно формировать произвольные логические выводы. Причем, для этого достаточно двухслойной НС. Хотя, как я уже отмечал, многослойные оказываются гораздо более практичным решением. Следует отметить, что функцию XOR также можно было бы реализовать и другим подходом, по формуле:
Но здесь используется умножение двух признаков. Выполнить эту операцию нейроном невозможно, т.к. там используется сумматор. Но мы могли бы сами заранее сформировать новый признак и подать на вход нейрона вектор:
Тогда операция XOR могла бы быть описана также с помощью одного нейрона. Оба подхода на практике вполне применимы. На этом мы завершим первое краткое теоретическое введение в НС. Более подробную информацию по нейронным сетям смотрите в плейлистах. А на следующем занятии мы подробно рассмотрим алгоритм back propagation для обучения НС. Видео по теме |
нейронов
скрытого слоя подаются на следующий слой (выходной в нашем примере) и
формируются M выходных
значений НС:
была
нелинейной? Если взять ее линейной, например,
.
Наиболее часто используют, следующие:
на
n-мерном
единичном кубе 
с
любой заданной точностью 
:
можно
описать функции И, ИЛИ, НЕ, XOR, следующим образом:
