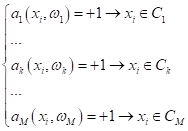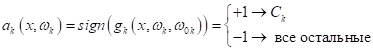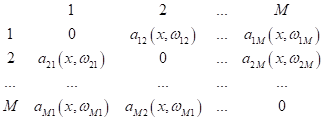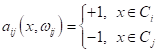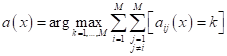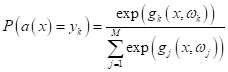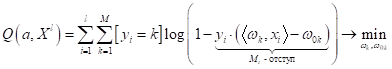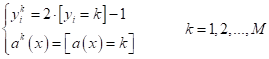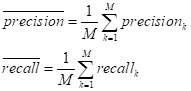SVM, PCA, показатели качества
Введение в метод опорных векторов (SVM)
Реализация метода опорных векторов (SVM)
Метод опорных векторов (SVM) с нелинейными ядрами
Вероятностная оценка качества моделей
Показатели precision и recall. F-мера
Метрики качества ранжирования. ROC-кривая
Метод главных компонент (Principal Component Analysis)
Сокращение размерности признакового пространства с помощью PCA
Сингулярное разложение и его связь с PCA
Многоклассовая классификация. Методы one-vs-all и all-vs-all
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
SVM, PCA, показатели качества

Многоклассовая классификация. Методы one-vs-all и all-vs-all

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

До сих пор мы с вами рассматривали только двухклассовую (бинарную) классификацию. Однако, на практике немало задач, когда нужно отнести объект к одному из M классов. Например, определение марок машин по их изображениям, или вида животных по их характеристикам и т.п. О способах решения таких задач мы с вами и поговорим на этом занятии.

Самый очевидный подход – это взять какой-либо алгоритм бинарной классификации и расширить его на M классов. Здесь существует множество стратегий, но наиболее распространенные две, известные под названиями:

one-vs-all (один против всех) – в ScLearn one-vs-rest;
all-vs-all (все против всех).

В первом случае (one-vs-all) мы строим M алгоритмов, которые отделяют один определенный класс от всех остальных:

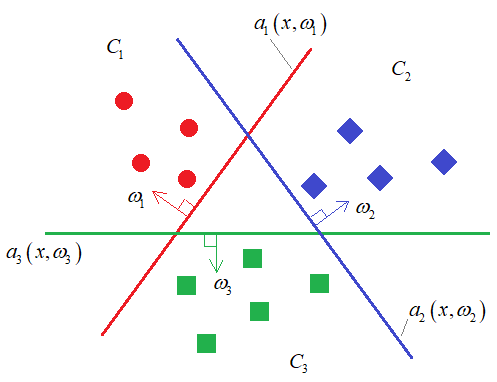
Например, если нарисовать в двумерном признаковом пространстве объекты трех классов (M=3), то каждый алгоритм будет определять свою разделяющую гиперплоскость, для выделения одного класса от всех остальных:

Причем, векторы весов подбираются так, чтобы положительное значение классификатора соответствовало принадлежности объекта определенному классу:

В частности, для линейных моделей:

После того, как модели обучены, выбор делается в пользу класса с самым большим положительным отступом от разделяющей границы:

И, обратите внимание, чтобы этот многоклассовый вывод работал корректно, длины векторов должны совпадать (это условие можно записать также через квадрат нормы):

Вот принцип работы стратегии один против всех (one-vs-all). Главным его недостатком является то, что мы обучаем каждую модель независимо от других моделей. Это несколько ухудшает конечный результат многоклассовой классификации.

Стратегия all-vs-all (все против всех)

Чтобы как то преодолеть недостаток предыдущей стратегии, была предложена другая, в которой модели выполняют бинарную классификацию только для пары классов:

(здесь M – число классов). То есть, модель, разделяющая два класса , формирует следующие выходные значения:

Причем, при правильном выборе моделей, очевидно, должно выполняться условие:

так как это, фактически, одна и та же, только «перевернутая» разделяющая гиперплоскость. С учетом этого равенства, мы получаем:

уникальных моделей. Затем, итоговый результат классификации для M классов определяется путем голосования (по мажоритарному принципу):

Многоклассовая логистическая регрессия

Для всех этих алгоритмов многоклассовой классификации можно применить формулу SoftMax:

для оценки вероятности принадлежности прогноза модели k-му классу. Однако, здесь следует быть аккуратными с интерпретацией полученных значений вероятностей. Как мы с вами уже говорили (когда рассматривали метод опорных векторов), эти вероятности в целом соответствуют реальным данным для логистической регрессии (при логарифмической функции потерь). Если же модель реализует какой-либо иной алгоритм бинарной классификации, то значения функции SoftMax могут сильно расходиться с их вероятностной интерпретацией. Поэтому, если вам действительно нужно получить вероятностные характеристики, то следует использовать многоклассовую логистическую регрессию, которую можно получить путем минимизации следующего функционала:

Забегая вперед, отмечу, что задача разделения образов на несколько классов, достаточно хорошо решается с помощью нейронных сетей. Однако, нейронные сети имеет смысл применять только для тех задач, где они действительно эффективны в сравнении с другими алгоритмами. Прежде всего, это задачи с трудно формализуемыми вторичными признаками, например, классификация изображений, звуков, анализ текста и прочее. Если признаки четко определяют решение поставленной задачи, то классические методы, как правило, проще (с вычислительной точки зрения) и приводят к схожим результатам, что и нейронные сети.

Метрики качества

В заключение этого занятия скажу пару слов о том, как оценивать качество моделей при многоклассовой классификации.

Самая распространенная метрика accuracy (доля верных классификаций), определяется абсолютно по той же формуле, что и для бинарного случая:

Но, как мы уже знаем, она не дает полную характеристику модели. Для более полной картины можно сформировать, так называемую, матрицу ошибок классификации:

	y=1	…	y=M
		…
…	…	…	…
		…

Здесь - число ответов модели класса i, когда в действительности имеет место класс j:

По этой матрице можно увидеть, как классификатор ведет себя на разных классах и сколько совершает ошибок.

Обобщения precision, recall, AUC-ROC при нескольких классах

Наконец, мы можем применить известные нам метрики precision, recall и AUC-ROC для многоклассового классификатора . Для этого, сначала приводят общую модель к бинарному виду для анализа классификации k-го класса:

А, затем, для каждого класса вычисляют характеристики:

После этого делают микро-усреднение этих показателей:

с последующим вычислением precision и recall:

Либо, выполняют макро-усреднение:

а уже затем, вычисляют средние показатели:

Отличия в микро- и макро-усреднениях достаточно просты. Из формул хорошо видно, если классы объектов в обучающей выборке не сбалансированы, то при микро-усреднении они будут «теряться». Тогда как при макро-усреднении они будут иметь примерно тот же вес, что и большие (по числу объектов) классы. То есть, если нам важны, при оценке модели, и большие и малые классы, то лучше использовать макро-усреднение. Если же, главным образом, анализируем большие классы, то микро-усреднение. Если же выборка сбалансирована, то различий между этими подходами особых нет.