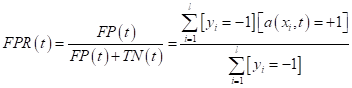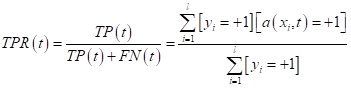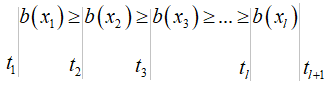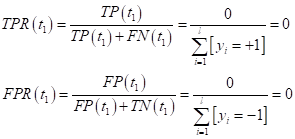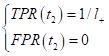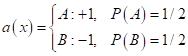SVM, PCA, показатели качества
Введение в метод опорных векторов (SVM)
Реализация метода опорных векторов (SVM)
Метод опорных векторов (SVM) с нелинейными ядрами
Вероятностная оценка качества моделей
Показатели precision и recall. F-мера
Метрики качества ранжирования. ROC-кривая
Метод главных компонент (Principal Component Analysis)
Сокращение размерности признакового пространства с помощью PCA
Сингулярное разложение и его связь с PCA
Многоклассовая классификация. Методы one-vs-all и all-vs-all
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
SVM, PCA, показатели качества

Метрики качества ранжирования. ROC-кривая

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

Продолжаем знакомиться с метриками качества оценок моделей при бинарной классификации. И на этом занятии мы затронем вопрос весьма важный вопрос оценки качества моделей ранжирования. Но вначале определимся, что это за класс моделей.

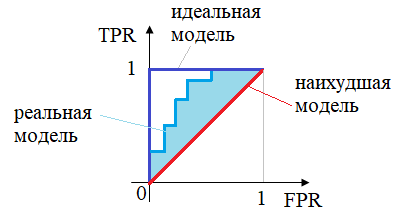
Рассмотрим классический пример удержания клиентов банка, сотового оператора или еще какой-либо организации. Нам поставили задачу по разработке модели, которая бы прогнозировала по некоторым признакам , что клиент скоро покинет учреждение (для определенности банк):

Конечно, модель делает лишь предположение. Уйдет клиент на самом деле или нет нам неизвестно. Мы можем это узнать только спустя какое-то время. Но на всякий случай таких «неуверенных» клиентов было бы хорошо обзвонить и сделать им «приятное» предложение, чтобы удержать. Однако, ресурсы любой организации ограничены и обзванивать всех таких клиентов может оказаться очень накладно. Поэтому здесь лучше выделить самых «неуверенных», которые с наибольшей вероятностью собираются перейти в другой банк. И возникает вопрос, как определить этих самых «неуверенных»? Для этого поступают следующим образом. Сортируют всех клиентов по значениям скалярного произведения:

Получаем таблицу:

	Реальный исход
100	+1
98	+1
76	+1
75	-1
…	…
50	+1
25	+1
10	-1
6	-1
4	+1
1	-1
-8	+1
-10	-1
-14	-1
…	…

Здесь самые первые (верхние) клиенты – это наиболее «неуверенные», те, что с наибольшей вероятностью покинут учреждение в ближайшем будущем, а чем ниже, тем все более лояльные. Причем, мы можем по историческим данным (или спустя какое-то время) определить, как реально себя повел тот или иной клиент (ушел или остался) – это целевые значения .

Так вот, при ограниченных ресурсах call-центра, было бы логично выделить в этой таблице несколько первых клиентов и именно им делать предложение, от которого они не смогут отказаться и, таким образом, удержать их. Математически это можно записать, следующим образом:

Здесь t – это некоторый порог (число), по которому разделяются клиенты на нелояльных (+1) и лояльных (-1). Устанавливая, например, этот порог больше нуля, мы будем выделять наименее лояльных клиентов с точки зрения модели. Причем, пороговое значение – это переменная величина и может меняться, выделяя более или менее лояльных клиентов, например, в зависимости от нагрузки call-центра. В этом ключевая особенность работы алгоритмов ранжирования. Нам приходится разрабатывать модель, не зная конкретного порогового значения, то есть, она в целом (для любых порогов) должна давать хорошие прогнозы поведения пользователей. Например, если при некотором пороге t, упорядоченные по убыванию значения скалярного произведения, будут соответствовать чередованию целевых значений на исторических данных, значит, модель делает плохой прогноз и эффективность работы учреждения, скорее всего, резко снизится. Поэтому, прежде чем применять модель на практике, ее нужно оценить и, обычно, делается это с помощью разработанных метрик качества ранжирования.

ROC-кривая

Вообще, идеальная модель ранжирования – это та, у которой после сортировки целевые значения также оказываются отсортированными по не возрастанию (сначала все +1, затем, все -1). Тогда, для любого порога t мы будем получать качественные результаты. Но это в идеале. В реальности же существуют ошибки и в этих условиях нужно понять, как будет строить прогнозы модель при разных порогах t. Для этого поступают, следующим образом. Используют две характеристики качества классификации модели:

False Positive Rate – доля ошибочных положительных классификаций:

Величину еще называют специфичностью алгоритма.

True Positive Rate – доля правильных положительных классификаций (чувствительность алгоритма):

Внимательный зритель здесь сразу отметит, что метрика

то, что мы рассматривали на предыдущем занятии. Причем, формально величины можно вычислять не только для линейных алгоритмов классификации, но и для любых других, главное, чтобы мы имели возможность ранжирования с использованием порога.

Итак, у нас есть две характеристики , которые зависят от свободного параметра t. Как теперь с их помощью оценить модель для задачи ранжирования? Для этого строят график, который исторически (из радиотехники) получил название Receiver Operating Characteristic или сокращенно ROC-кривая. График строится в осях TPR/FPR:

Для этого мы будем перебирать значение параметра t в диапазоне:

где , - бесконечно малая величина.

Сначала выбираем порог . Он больше всех возможных значений скалярного произведения в нашей выборке. Следовательно:

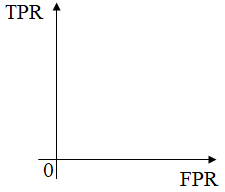
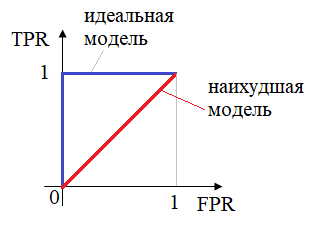
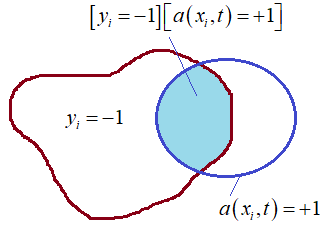
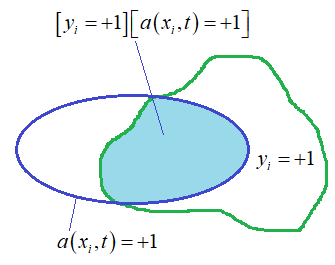
Получаем, что график ROC-кривой исходит из нуля (0; 0). Далее предположим, что у нас идеальная модель, т.е. она не совершает ошибок (полностью совпадает с целевыми значениями ). Тогда для следующего порога мы получим некоторое увеличение и нулевое значение для :

(здесь - число объектов положительного класса). Перебирая дальше пороги, мы, очевидно, будем постоянно увеличивать TPR, сохраняя нулевое значение FPR, пока не переберем все объекты положительного класса. В этом случае TPR достигнет максимального значения 1, а FPR пока будет равно нулю.

Далее, переходя к отрицательным классам, у нас все будет наоборот – TPR остается без изменений, равный 1, а FPR станет постепенно увеличиваться, доходя до 1. В результате, для идеальной модели график ROC-кривой будет иметь вид (синяя линия):

А вот для наихудшей модели, которая прогнозирует значения бинарного класса с вероятностью 1/2:

ROC-кривая будет примерно лежать на диагонали (красная линия).

Как вы уже догадались, реальные модели с небольшим числом ошибок прогнозов, лежат между красной и синей кривыми:

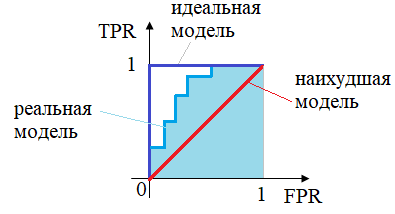
Отлично, ROC-кривую мы научились строить, но как теперь по ней получить числовую характеристику качества модели? Здесь есть два распространенных подхода. В первом случае просто берут площадь под ROC-кривой. Такая характеристика называется AUC-ROC, и чем она больше, тем качественнее модель. Для идеальной модели площадь равна 1, а для худшей – 1/2. Хорошими считаются модели, у которых площади больше 0,9. То есть, показатель AUC-ROC показывает, насколько хорошо модель сортирует (ранжирует) объекты класса.

Во втором случае вычисляют меру разности площадей между ROC-кривыми реальной модели и наихудшей, по следующей формуле:

То есть, это удвоенная разность между площадью ROC-кривой анализируемой модели и наихудшим случаем:

Такой показатель называют индексом Джини или коэффициентом Джини. Но это лишь несколько иной взгляд на ту же самую площадь под ROC-кривой.

Основным недостатком этих показателей (AUC-ROC и индекс Джини) является плохой учет в их значениях несбалансированности классов. Например, если к положительному класс относятся 100 объектов, а к отрицательному 1 000 000, то площадь под ROC-кривой получится большой (выше 0,9), но при этом ранжирование объектов может быть очень плохим. Вот этот момент следует учитывать, пользуясь данными характеристиками качества ранжирования.

Практический курс по ML: https://stepik.org/course/209247/

Метрики качества ранжирования. ROC-кривая

ROC-кривая

Видео по теме