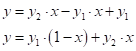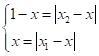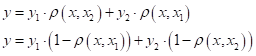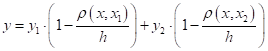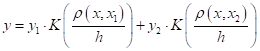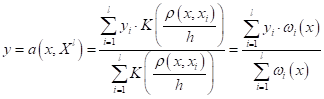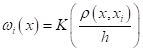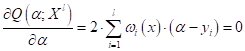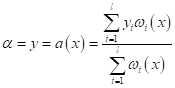|
Метрические регрессионные методы. Формула Надарая-ВатсонаПрактический курс по ML: https://stepik.org/course/209247/ На предыдущих занятиях мы увидели, как можно использовать метрический подход для построения классификаторов. Но его же можно применять и в задачах регрессии, когда выходом модели является не номер класса, а некоторое вещественное значение:
Давайте
предположим, что у нас имеется некоторый набор размеченных данных
В таких задачах
модель
и находили
вектор параметров
то автоматически
приходим к методу наименьших квадратов (МНК). Здесь Существенным
недостатком такого подхода является необходимость выбора параметрической
функции
между
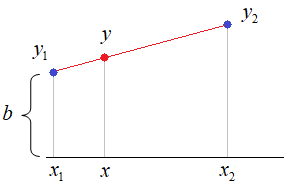
произвольным отсчетом Давайте, я покажу принцип такого подхода на простом примере линейной аппроксимации данных из двух точек:
Здесь все промежуточные значения можно вычислить по формуле прямой:
Для простоты положим, что:
Тогда:
Эту же формулу можно переписать в виде:
Смотрите, здесь
расстояния до
соседних точек
В этих
обозначениях величину
А обобщение на произвольный интервал
даст выражение:
Вам это ничего
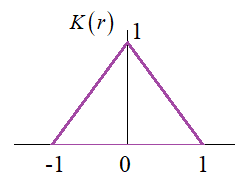
не напоминает? Смотрите, здесь веса перед
Получим:
Или, обобщая на произвольное число отсчетов, имеем:
В последнем равенстве введено обозначение весовых коэффициентов:
Также обратите внимание, мы здесь в формулу добавили нормировку по весам, так как при большем числе отсчетов и при разных функциях ядра, нам необходимо сохранить масштаб выходных значений. Полученная нами формула известна под названием формулы ядерного сглаживания Надарая-Ватсона. Ее можно вывести более строгими математическими методами, например, из критерия минимума квадрата ошибки, при константной параметрической функции:
Дифференцируя это выражение по α, и приравнивая результат нулю, получим:
откуда
Этот простой вывод показывает, какой критерий качества минимизируется формулой Надарая-Ватсона. Общий вывод
здесь такой. Мы получаем возможность аппроксимировать экспериментальные
зависимости В качестве
функции ядра Примеры аппроксимации данных ядерным сглаживаниемВ заключение этого занятия я приведу программу на Python, которая реализует аппроксимацию данных с помощью формулы Надарая-Ватсона. Текст программы можно посмотреть по ссылке: Экспериментальные данные здесь генерируются по формуле:
где Затем, мы определим метрику как модуль расстояния:
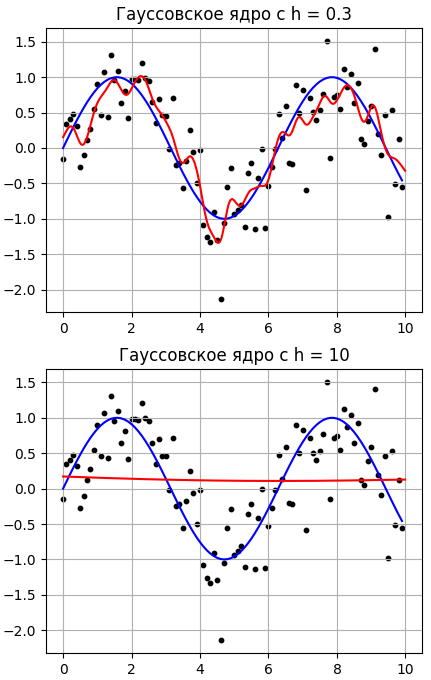
А в качестве ядра возьмем гауссовскую кривую:
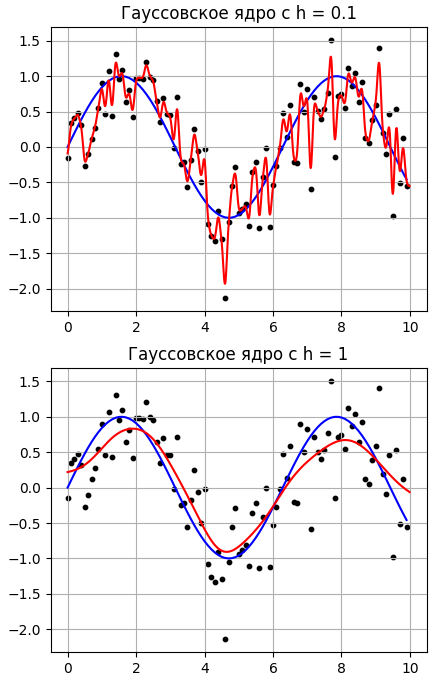
Получим следующие результаты при разной ширине окна h:
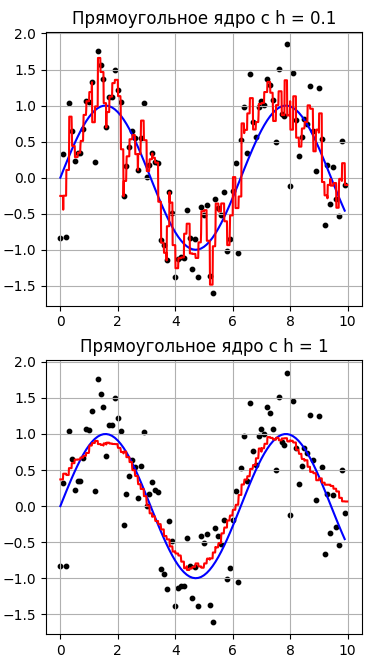
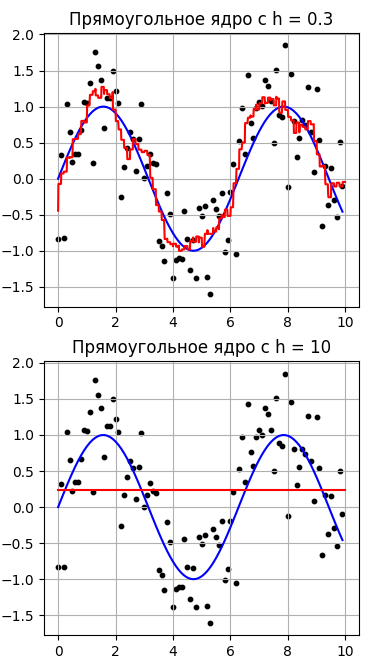
Как видим, лучшие результаты получаются при ширине окна h=1, причем, с ростом h у нас данные, фактически, усредняются. Давайте, теперь выберем прямоугольное окно и посмотрим, как будет выглядеть аппроксимация данных:
Здесь красная кривая выглядит уже не такой гладкой, т.к. используется не гладкая функция ядра. Во всем остальном принцип сохраняется: лучшее значение при h=1, а при h=10 имеем среднее арифметическое по всем выходным (целевым) значениям выборки. В обоих случаях малое значение h приводит к, своего рода, переобучению модели, т.к. мы слишком сильно подстраиваемся под выходные значения. Такая модель вряд ли будет давать хорошие прогнозы. С другой стороны, большое значение h слишком сильно огрубляет выходные значения и приводит к значительному расхождению между истинной зависимостью (синий график) и восстановленными значениями (красный график). На практике ширину окна h часто выбирают по результатам экспериментов, например, методом скользящего контроля leave-one-out (LOO):
Здесь мы последовательно из выборки убираем по одному наблюдению и строим его прогноз по всем остальным. То окно h, которое приводит к лучшим прогнозам, выбираем в качестве параметра результирующей модели. Вот, в целом, принцип решения регрессионных задач метрическими методами, которые приводя к формуле ядерного сглаживания Надарая-Ватсона. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
, связанных некоторой
зависимостью (не обязательно строго функциональной):
должна
уловить природу взаимосвязи между входами 
и
выходами 
.
Ранее, мы с вами решали эту задачу путем параметрической оптимизации. То есть,
предполагали зависимости в виде некоторой функции:
так,
чтобы обеспечить минимум функционала качества. Если функционал имеет вид:
-
веса слагаемых (степень их важности). В самом простом случае все их можно
приравнять единице.
.
Она должна корректно отражать зависимость 
данных.
И эта зависимость не всегда очевидна. В этом случае на решение этой же задачи
можно посмотреть с другой стороны. Если нам не составляет труда задать метрику:
и
значениями 
,
то можно применить метрические методы аппроксимации выходных значений 
.
,
то есть, фактически, метрика:
можно
определить, следующим образом:
можно
выразить через треугольное ядро:
через
определение метрики 
и
функции ядра 
.
В результате мы ушли от явного определения параметрической функции 
-
гауссовские случайные величины с нулевым средним и дисперсией 0,5. Сами же
величины 
с
шагом 0,1.
