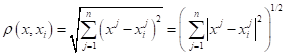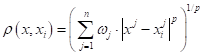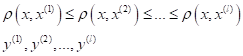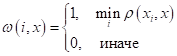Метрические методы
Метрические методы классификации. Метод k ближайших соседей
Методы парзеновского окна и потенциальных функций
Метрические регрессионные методы. Формула Надарая-Ватсона
Задачи кластеризации. Постановка задачи
Алгоритм кластеризации Ллойда (K-средних, K-means)
Алгоритм кластеризации DBSCAN
Агломеративная иерархическая кластеризация. Дендрограмма
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
Метрические методы

Метрические методы классификации. Метод k ближайших соседей

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

На этом занятии мы начнем рассматривать метрические методы классификации. Вначале небольшое, краткое введение. В 1936 году Рональд Фишер, специалист по математической статистике, представил работу по анализу данных цветков ирисов. Данные были собраны ботаником Эдгаром Андерсоном, а Фишер нашел способ по этим данным классифицировать три вида ирисов:

ирис щетинистый (iris setosa);
ирис виргинский (iris virginica);
ирис разноцветный (iris versicolor).

Ирисы Фишера, как их стали позже называть, состоят из данных о 150 экземплярах и результатов, следующих измерений:

длина наружной доли околоцветника (sepal length);
ширина наружной доли околоцветника (sepal width);
длина внутренней доли околоцветника (petal length);
ширина внутренней доли околоцветника (petal width).

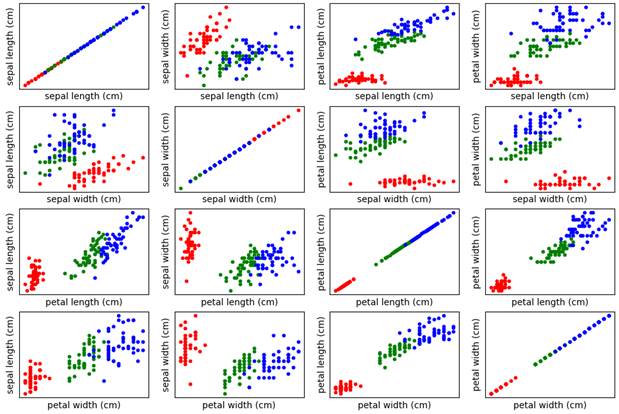
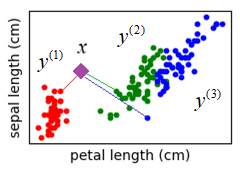
Эти данные можно воспринимать как четырехмерное признаковое пространство, в котором представлены объекты трех классов (трех видов ирисов). Для их визуализации используется, так называемая, диаграмма рассеяния ирисов Фишера. Это отображение всех попарных наборов признаков:

Из этих рисунков хорошо видно, что объекты (результаты измерений) одного и того же класса лежат, как правило, близко друг к другу. И это довольно частая ситуация. В последствие была выдвинута гипотеза компактности, которая гласит:

Координаты образов одного и того же класса в признаковом пространстве концентрируются в геометрически близкие точки, образуя «компактные» сгустки.

Это именно гипотеза. Не для всех объектов она выполняется. Мы это можем лишь предполагать. Но если анализ признакового пространства показывает, что гипотеза компактности, в целом, выполняется, то для задач классификации можно применять, так называемые, метрические методы.

Метрические методы – это методы, которые основаны на расстояниях (меры близости) конкретного образа до образов других классов в признаковом пространстве. Например, у нас есть результат измерения (ромб). Тогда, было бы логично отнести его к тому виду (группе точек), к которому он ближе всего:

Но здесь сразу возникают две проблемы:

как измерять расстояния между объектами в признаковом пространстве;
как определять на основе вычисленных расстояний принадлежность объекта к той или иной группе точек.

На эти вопросы нет единого, общего ответа. А потому существует множество различных метрических методов классификации.

Метрики в пространстве признаков

Давайте начнем с первого вопроса – способа определения расстояния между двумя любыми векторами в n-мерном признаковом пространстве . Предположим, у нас имеются векторы объектов размеченных данных:

и новые результаты измерений, которые следует классифицировать:

Тогда, первое, что приходит в голову, взять евклидовое расстояние между двумя точками:

И такая метрика, действительно, применяется на практике. Но единственная ли она возможная? Конечно, нет. В самом простом случае, мы можем обобщить евклидову метрику, следующим образом:

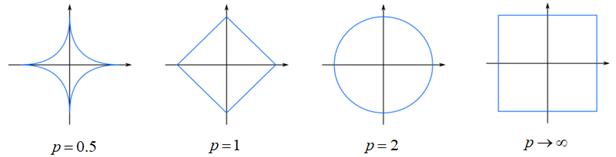
Здесь - параметр метрики; - веса признаков. Такой общий способ вычисления расстояний называется метрикой Минковского.

Зачем нужны веса в этой формуле? Дело в том, что признаки могут иметь разный масштаб. Например, вес золота в граммах и его стоимость в рублях – это два совершенно разных диапазона значений. Чтобы их в равной степени учитывать при определении близости векторов, следует нормировать через подбор весовых коэффициентов.

Другой параметр p задает поведение метрики в разных направлениях. Это проще всего показать на рисунках эквидистантных кривых:

Как видим, при p=1 имеем аналог суммы разностей модулей координат, при p = 2 – классическое евклидовое расстояние, а если , то круг вырождается в квадрат. Чаще всего на практике можно увидеть метрику с модулями и квадратами (при p = 1 и 2).

Обобщенный метрический классификатор

После того, как метрика введена, мы можем строить алгоритм классификации на основе критерия близости некоторого объекта к размеченным образам (ее можно воспринимать, как обучающую выборку). Для этого удобно все объекты выборки упорядочить по возрастанию расстояния относительно совместно с целевыми значениями:

(верхний индекс – новый порядок наблюдений в выборке). Тогда математически классификатор в самом общем виде можно записать, следующим образом:

где - вес (степень важности) i-го объекта по отношению к , связанный с метрикой . Величина неотрицательная и не возрастает при увеличении i.

Фактически, здесь, мы вычисляем суммарный вес для каждого класса и выбираем класс с наибольшей суммой.

Метод k ближайших соседей (k nearest neighbors, kNN)

Давайте, для лучшего понимания конкретизируем эту формулу для простейшего случая, когда мы полагаем:

(помним, что образы упорядочены по возрастанию расстояний относительно вектора ). То есть, у нас i-й вес принимает единичное значение для самой ближайшей точки, и нулевые – для всех остальных:

В этом случае модель можно записать в виде:

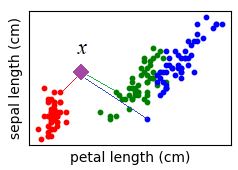
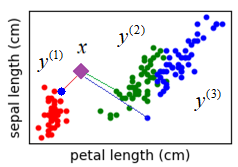
То есть, мы относим объект к классу объекта с минимальным расстоянием в соответствии с выбранной метрикой :

Этот метод известен под названием метод ближайшего соседа. Очевидно, у него есть существенный недостаток. Если среди образов одного класса случайно окажется представитель другого класса, до которого расстояние минимально, то классификатор сделает неверный вывод:

Побороть такие единичные выбросы относительно просто, если учитывать не одного, а k ближайших соседей. В этом случае вектор весов можно определить по правилу:

То есть, теперь веса будут принимать единичные значения для первых k ближайших векторов, а остальные оставаться нулевыми. В результате мы приходим к методу k ближайших соседей со следующим алгоритмом классификации:

По простому, мы предпочтение отдаем тому классу, для которого число из k ближайших соседей наибольшее:

Например, если в окрестности объекта семь образов, причем 4 относятся к классу , а 3 – к классу , то делаем вывод, что объект принадлежит первому классу, т.к. его представителей больше.

Недостатки методов ближайших соседей

Конечно, здесь сразу виден недостаток такого подхода: что делать, если представителей обоих классов будет поровну? Какому классу тогда отдать предпочтение? Можно попробовать взять нечетное число k, тогда для двух классов эта проблема будет решена. Но, ведь в окрестности может оказаться и три и четыре разных классов. Поэтому, эта общая проблема существует и не имеет однозначного решения.

Другим важным недостатком являются единичные значения весов для ближайших k образов:

То есть, мы не учитываем расстояния до соседних объектов, только их наличие или отсутствие. А, наверное, было бы логично оперировать, в том числе, и расстояниями.

Далее, мы с вами познакомимся с другими метрическими алгоритмами классификации, которые решают эти проблемы, хотя порождают некоторые другие. В конце концов, универсальных решений нет.

Преимущества метода k ближайших соседей

Несмотря на очевидные недостатки, метод k ближайших соседей получил широкое распространение и в ряде задач показывает хорошие результаты. Главным его преимуществом является простота реализации. Нам достаточно выделить k ближайших объектов и выделить класс с максимальным числом представителей. Вычислительно, это очень просто. Здесь даже нет, как такового, алгоритма обучения. Все, что нам нужно – это иметь массив размеченных данных (представителей классов) и по ним, затем, относить новые объекты к тому или иному классу. Это называется lazy learning (ленивое обучение).

Благодаря простоте реализации, мы можем на обучающей выборке применить технику скользящего контроля leave-one-out (LOO) для нахождения наилучшего параметра k. Я напомню, что при LOO мы последовательно убираем из выборки по одному образу и оцениваем качество его прогнозирования выбранной моделью (алгоритму классификации) по оставшейся выборке. Так как наша модель в методе k ближайших соседей зависит от параметра k:

то его можно подбирать по методу LOO так, чтобы алгоритм совершал как можно меньше ошибок:

Даже для больших выборок в сотни тысяч и миллион наблюдений можно перебрать целые значения k, скажем в диапазоне от 1 до 100 и выбрать тот, который даст минимум функции LOO.

Я, надеюсь, из этого занятия вы поняли, что из себя в целом представляют метрические методы классификации и как работает алгоритм k ближайших соседей.