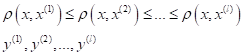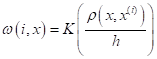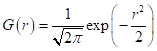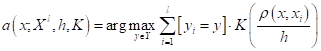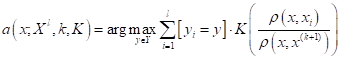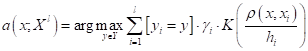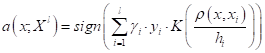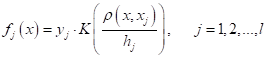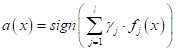|
Методы парзеновского окна и потенциальных функцийПрактический курс по ML: https://stepik.org/course/209247/ На предыдущем
занятии мы с вами рассмотрели простейший алгоритм метрической классификации k ближайших
соседей. И отметили существенный недостаток его весовых коэффициентов
они принимают только два значения:
Я напомню, что
индекс i означает i-й образ в
упорядоченной по возрастанию расстояний последовательности относительно
классифицируемого вектора
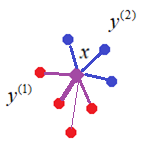
То есть, формула
просто выделяет k ближайших
соседей для вектора
(близкие соседи
несут больший вклад, чем далекие). Для реализации этой идеи веса
Причем, часто ее выбирают ограниченной (финитной) на интервале [0; 1] и симметричной относительно нуля (четной):
Такие ядра получили название окно Парзена или парзеновские окна. Для окон
параметр h в формуле весов
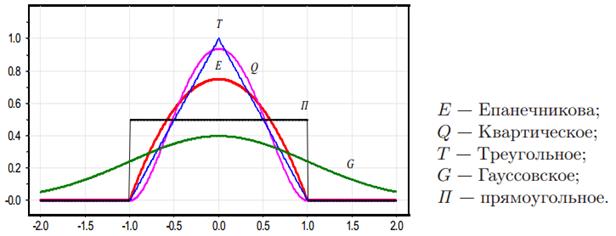
определяет область охвата объектов относительно вектора Остается вопрос, какую функцию ядра взять? Часто на практике используют следующие варианты:
Здесь В результате, мы получаем следующий алгоритм классификации с помощью парзеновского окна:
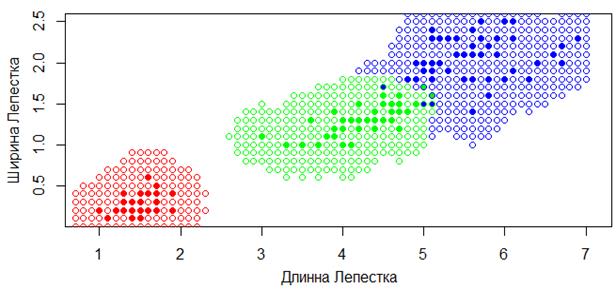
Здесь мы уже можем не сортировать наблюдения по расстояниям, т.к. функция расстояния используется в самом ядре. Фактически, алгоритм работает по похожему принципу, что и метод k ближайших соседей, только рассматривает всех соседей на расстоянии h и с учетом расстояния до них. Например, вот так выглядит карта классификации для квадратического парзеновского окна с параметром h=0,4 в пространстве двух признаков для цветов ирисов:
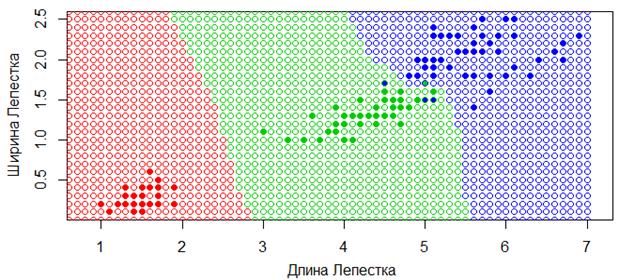
В сравнении та же карта классификации для метода k ближайших соседей при k=6, выглядит следующим образом:
Видите, как заметно отличаются результаты моделей при этих двух подходах. И, наверное, более логичные результаты, мы получаем именно при использовании парзеновских окон, так как области принятия решений становятся ограниченными, как и должно быть в большинстве задач классификации. Однако, у рассмотренного подхода есть один существенный недостаток. Нам нужно как то выбирать параметр h для каждой конкретной задачи. Сделать это можно двумя способами. В первом поступить также, как мы делали в задаче k ближайших соседей, используя метод leave-one-out (LOO):
То есть, поочередно отбрасываем по одному наблюдению из обучающей выборки и оцениваем качество классификации по оставшимся данным при заданном значении параметра h. Затем, меняем h и повторяем эту процедуру. По полученным результатам выбираем h, который приводит к меньшему числу ошибок на обучающей выборке. Второй вариант – это
«скрестить» метод k ближайших
соседей с парзеновским окном. Если считать, что ядро
и алгоритм классификации принимает вид:
Правда, здесь
нам снова придется вернуться к идее упорядочивания наблюдений по возрастанию
расстояний, чтобы определить ширину окна для каждого конкретного вектора Однако, этот
второй подход, как правило, дает лучшие результаты, чем окна с фиксированной
шириной. Особенно актуально это для тех задач, в которых плотность (кучность)
объектов разных классов разная. Тогда подобрать адекватно фиксированную ширину
не всегда удается, а вот адаптивный выбор ширины Ну а общим
недостатком этих методов является необходимость выбора ядра Метод потенциальных функцийНемного другой
взгляд на алгоритмы метрической классификации дает метод потенциальных функций.
Здесь рассуждения идут не относительно классифицируемого вектора
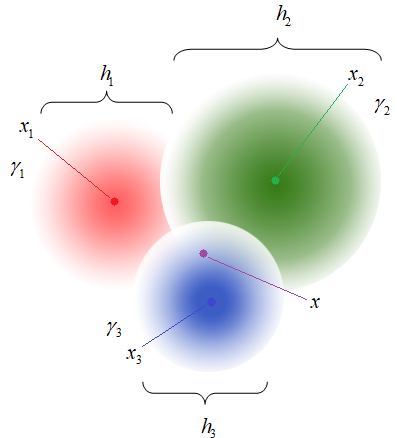
Каждый объект
выборки Математически этот алгоритм можно записать, следующим образом:
где Недостатком и в
то же время преимуществом такого подхода является большое число настраиваемых
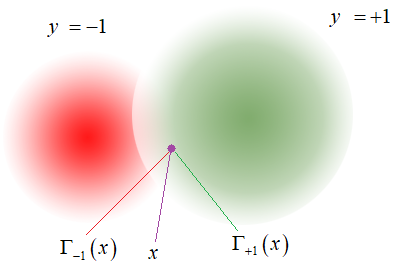
параметров Метод потенциальных функций при бинарной классификацииИнтересную интерпретацию метода потенциальных функций можно сделать для бинарной классификации, когда у нас всего два класса с метками:
В этом случае, у
нас в точке
Здесь
или так:
В последней
формуле значение разности суммарных потенциалов достигается за счет меток
классов Если теперь выделить выражение:
то его можно
воспринимать как формирование нового признака для j-го объекта
обучающей выборки. Причем, этот признак формируется, как функция от расстояния
между классифицируемым вектором
Что вам
напоминает эта формула? Да, это общая запись линейного алгоритма бинарной
классификации образов. А Этот пример показывает,
что мы можем создавать новые признаки для объектов Итак, на этом занятии мы с вами рассмотрели два очевидных обобщения простейшего метрического алгоритма k ближайших соседей:
Преимущества всех метрических алгоритмов в простоте их реализации. Правда, при этом нужно хранить всю выборку размеченных данных (обучающую выборку), по которым и осуществляется дальнейшая классификация. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
:
:
до
них: чем оно больше, тем меньший вес должно иметь данное наблюдение.
(ее
еще называют ядром):
-
индикатор того, что 
,
то есть, возвращается 1, если это так и 0 – в противном случае.
обучающей
выборки:
и
интенсивностями 
.
Все, что нам остается, это в точке 
-
веса i-х объектов
(интенсивности); 
-
мера ширины распределения значений ядра 
.
В самом простом случае их можно считать равными и выбрать некоторые значения h и γ. Либо,
если у нас есть некоторые «знания» о свойствах объектов выборки, то всегда
можно тонко настроить эти параметры для каждой группы объектов.
-
суммарный потенциал от объектов класса 
,
а 
-
суммарный потенциал от объектов класса 
.
Тогда алгоритм принятия решения можно записать через знаковую функцию:
.
Для всех объектов класса +1 получаем обычную сумму, а для объектов класса -1 –
сумму со знаком минус. В итоге имеем суммарную разность потенциалов объектов
обоих классов.
.
Далее, автоматически получаем следующий алгоритм классификации:
-
набор весовых коэффициентов, определяющих ориентацию гиперплоскости в
пространстве признаков. В нашем случае число признаков получается равным
размеру всей обучающей выборки. Но мы можем их сократить, если, например,
подбирать коэффициенты 
