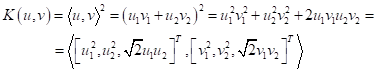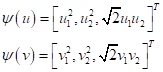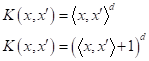SVM, PCA, показатели качества
Введение в метод опорных векторов (SVM)
Реализация метода опорных векторов (SVM)
Метод опорных векторов (SVM) с нелинейными ядрами
Вероятностная оценка качества моделей
Показатели precision и recall. F-мера
Метрики качества ранжирования. ROC-кривая
Метод главных компонент (Principal Component Analysis)
Сокращение размерности признакового пространства с помощью PCA
Сингулярное разложение и его связь с PCA
Многоклассовая классификация. Методы one-vs-all и all-vs-all
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
SVM, PCA, показатели качества

Метод опорных векторов (SVM) с нелинейными ядрами

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

На предыдущем занятии я отметил, что для линейного бинарного классификатора вида:

коэффициенты ω в методе опорных векторов могут быть вычислены по формуле:

где - некоторые коэффициенты. Причем ненулевые коэффициенты соответствуют опорным или ошибочным векторам (выбросам).

Если объединить эти две формулы, то получается, что:

(здесь сумма взята не по всем объектам, а только по опорным, для которых ).

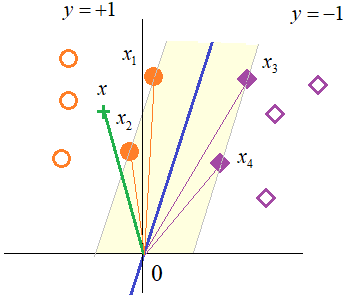
Отсюда хорошо видно, что классификатор вычисляет взвешенную сумму скалярных произведений опорных векторов с некоторым входным вектором x, вычитает смещение b и определяет знак. Графически это выглядит, так:

Пусть у нас линейно разделимая выборка с четырьмя граничными векторами . Смещение для простоты приравняем нулю (). Тогда для произвольного вектора будет вычисляться следующая линейная комбинация:

Или, ее можно записать в таком виде. Сначала суммируем опорные векторы для одного и второго классов образов:

А, затем, на который из них приходится наибольшая проекция вектора x:

Классификатор просто берет знак от этой величины и выдает свое решение:

Вот так можно интерпретировать работу линейного бинарного классификатора в методе опорных векторов.

SVM с нелинейными ядрами

Но давайте вернемся к общей формуле модели линейного классификатора:

и зададимся вопросом, а что если линейные преобразования:

в исходном признаковом пространстве заменить какими-либо нелинейными? Например, взять, и возвести это скалярное произведение в квадрат:

Сможем ли мы тогда повторить все те же вычисления для нахождения опорных векторов и коэффициентов ? Оказывается да, для указанного преобразования и некоторого ряда других нелинейных преобразований решение системы методом Каруша-Куна-Таккера с использованием функции Лагранжа остается неизменным.

Вообще существует теорема, которая гласит:

Функция является ядром (подходит для задачи SVM) тогда и только тогда, когда она симметрична: и неотрицательно определена:

для любой .

Я привел эту теорему лишь формально. На практике ей руководствоваться достаточно сложно (как говорят, она не конструктивна). Но, в частности, преобразование:

удовлетворяет этой теореме. Давайте распишем его для двумерных векторов:

получим:

То есть, возведение скалярного произведения в квадрат двумерных векторов – это аналог скалярного произведения трехмерных векторов:

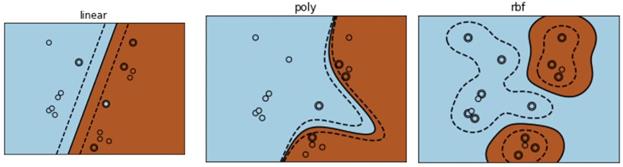
Фактически, функция формирует новое трехмерное признаковое пространство, в котором начинает работать обычный линейный алгоритм опорных векторов. Но с позиции исходного двумерного признакового пространства, мы получаем полиномиальные функции степени два. Причем полиномы здесь не произвольные, а состоят только из омонимов степени два (слагаемых меньших степеней здесь нет).

Я приведу характерные рисунки, взятые из официальной документации Scikit-Learn разделяющих гиперплоскостей для разных типов ядер:

Здесь linear – обычное скалярное произведение; poly – полиномиальное ядро, образуемое функциональными преобразованиями вида:

rbf – радиальные ядра, определяемые выражением:

В практике SVM еще можно встретить ядро вида:

На его основе получается аналог двухслойной нейронной сети с сигмоидальными функциями активации.

SVM как двухслойная нейронная сеть

Вас может немного удивить, причем здесь нейронная сеть, когда мы говорим о совершенно иной структуре алгоритма на основе разделяющей гиперплоскости? Но на самом деле SVM можно представить в виде следующей вычислительной структуры. Так как выход модели при произвольных ядрах вычисляется по формуле:

то имеем:

То на скрытом слое у нас вычисляются свертки входного вектора x с опорными векторами с учетом выбранного ядра . Затем, все эти значения умножаются на весовые коэффициенты , суммируются и пропускаются через знаковую функцию активации. Причем, SVM нам сразу определил необходимое число нейронов скрытого слоя и, конечно же, значения весовых коэффициентов. На мой взгляд, это очень здорово!

Способы синтеза ядер

В заключение этого занятия отмечу несколько простых правил синтеза ядер для метода опорных векторов. К основным можно отнести следующие подходы:

- скалярное произведение;
- константа;
- произведение ядер (подходящих для SVM);
- применение функции;
- сумма ядер.

Существуют и некоторые другие способы синтеза ядер. Но часто на практике использует довольно ограниченный класс – это линейные, полиномиальные, радиальные и гиперболический тангенс. Обычно их вполне хватает для большинства задач и именно такие ядра встроены в пакет Scikit-Learn для метода опорных векторов. Причем, для каждого типа ядра вычислительная схема SVM несколько меняется. Поэтому нельзя сформировать универсальный функционал для произвольных ядер (если, конечно, не использовать субградиентные методы).

Преимущества и недостатки SVM

Итак, если нам удается свести задачу к методу опорных векторов, то мы автоматически получаем следующие преимущества перед субградиентыми методами и нейронными сетями:

Здесь решается оптимизационная выпуклая задача квадратичного программирования, которая имеет одну точку минимума (единственное решение).
Позволяет выделить опорные векторы, в том числе и выбросы, которые могут присутствовать в обучающей выборке (иногда SVM применяют для нахождения выбросов).
В сравнении с нейронными сетями позволяет определить необходимое число нейронов скрытого слоя, как число опорных векторов.

Конечно, универсальных методов в природе не существует и SVM присущи ряд недостатков:

Нет общих подходов к задаче оптимизации для произвольных ядер .
Нет «встроенного отбора признаков» (аналог L1-регуляризатора).
Необходимо подбирать гиперпараметр C для каждой решаемой задачи.

Тем не менее, считается, что SVM является лучшим методом классификации среди прочих линейных классификаторов. Благодаря максимизации ширины полосы между классами, он, как правило, приводит к лучшим обобщающим способностям на реальных данных. Его относительно легко модифицировать для нелинейного случая (для разных ядер), а также дополнительно использовать L1-регуляризатор.