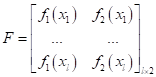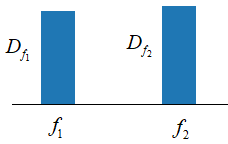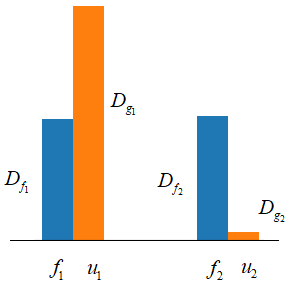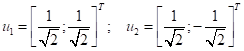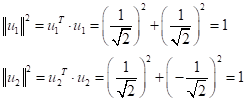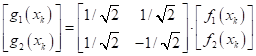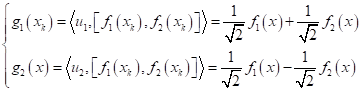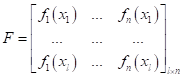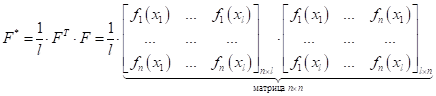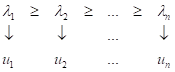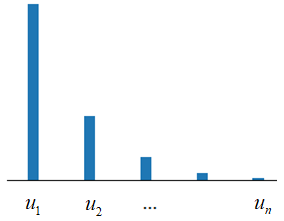SVM, PCA, показатели качества
Введение в метод опорных векторов (SVM)
Реализация метода опорных векторов (SVM)
Метод опорных векторов (SVM) с нелинейными ядрами
Вероятностная оценка качества моделей
Показатели precision и recall. F-мера
Метрики качества ранжирования. ROC-кривая
Метод главных компонент (Principal Component Analysis)
Сокращение размерности признакового пространства с помощью PCA
Сингулярное разложение и его связь с PCA
Многоклассовая классификация. Методы one-vs-all и all-vs-all
Обучающие курсы
Python Python ООП Django C/C++ ООП C++ Машинное обучение Структуры данных
Телеграм-каналы
Канал selfedu_rus Python Django Машинное обучение Java и С++
Наши каналы

Главная
ML
SVM, PCA, показатели качества

Метод главных компонент (Principal Component Analysis)

Практический курс по ML: https://stepik.org/course/209247/

Смотреть материал на YouTube | RuTube

Ранее мы с вами говорили, что одной из ключевых проблем в машинном обучении является эффект переобучения (overfitting). И для борьбы с ним предполагалось либо уменьшать признаковое пространство (упрощать модель), либо вводить регуляризаторы, или делать и то и то. С регуляризаторами в целом все понятно. А вот как можно сократить признаковое пространство, оставив только наиболее важные характеристики объектов, мы с вами подробно познакомимся на этом и последующих занятиях.

Давайте для простоты предположим, что у нас имеется обучающая выборка, состоящая из объектов, представленная в двумерном признаковом пространстве, которое в общем случае описывается функциями:

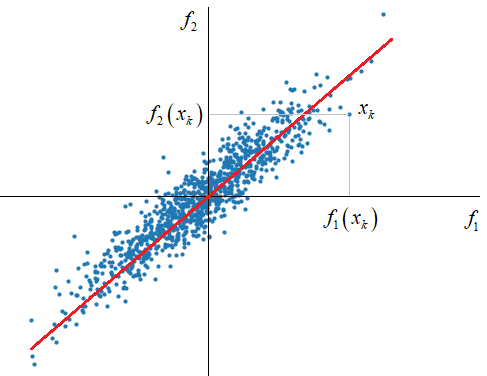
(В самом простом варианте можно считать, что). Пусть, для примера, множество объектов распределено около нуля и вытянуто вдоль линии под углом в 45 градусов:

Мы видим, что признаковое пространство изображено в виде декартовой системы координат и каждая точка (объект выборки) однозначно описывается двумя координатами:

Из этого рисунка хорошо видно, что разброс проекций точек на обе оси, примерно одинаков, с дисперсиями около 0,25:

При некоторых ограничениях, величины можно воспринимать, как среднее количество информации, приходящее на первую и вторую ось. То есть, для нашего примера распределения объектов признаки примерно равноинформативны.

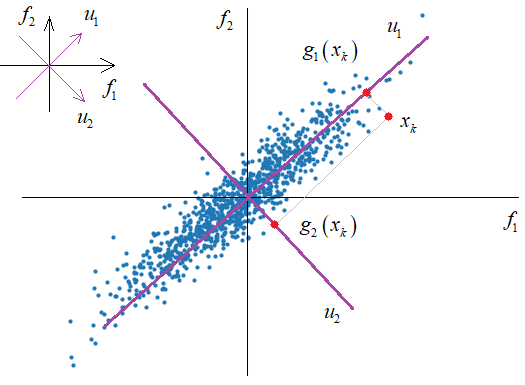
Давайте теперь подумаем, можно ли для нашего конкретного случая сформировать другую ортогональную систему координат так, чтобы на первую ось приходились, в среднем, наибольшие проекции векторов , а на вторую – оставшаяся часть? Почему бы нам не повернуть декартовую систему координат на 45 градусов по часовой стрелке:

Из этого рисунка хорошо видно, что, в среднем, наибольшая проекция будет приходиться на ось , а оставшаяся часть – на ось . То есть, у нас информация об объектах будет, в большей степени, концентрироваться в признаке и в меньшей степени – в признаке .

Новую систему координат можно описать с помощью следующих единичных векторов:

В этом случае квадрат нормы каждого вектора равен 1:

а, значит, они образуют ортонормированную систему координат. Теперь, любой вектор , представленный изначально в декартовых осях , можно представить в новом пространстве координатных осей , используя простое векторно-матричное умножение:

Или, при очевидных заменах, в виде:

То есть, мы ввели, для нашего конкретного случая, новое функциональное преобразование для признаков :

Причем, обратимое, теоретически, мы можем вернуться в исходное признаковое пространство, используя транспонированную матрицу собственных векторов:

Отлично, мы с вами научились концентрировать информацию о признаках для одного конкретного случая. Но как это сделать для произвольного распределения объектов ? Да и еще в многомерном пространстве, когда у нас не два, а n исходных признаков:

Оказывается, сделать это относительно просто. Для этого достаточно вычислить, так называемую, матрицу Грама по признакам:

А, затем, для нее найти собственные векторы и собственные числа, используя известное уравнение из линейной алгебры:

На языке Python это можно сделать с помощью пакета Numpy, командой:

L, W = np.linalg.eig(FF) # L – собственные числа; W – собственные векторы

В результате, получаем набор из n собственных векторов и, соответствующих им, n собственных чисел :

Собственные векторы образуют ортонормированную систему координат в n-мерном пространстве, а собственные числа равны дисперсиям проекций образов на соответствующие координатные оси.

Если отсортировать собственные векторы по убыванию собственных значений, то на первый вектор будут, в среднем, приходиться наибольшие проекции, на второй – наибольшая информация из оставшейся, и так до n-го вектора. Таким образом, мы получаем систему координат, которая наилучшим образом локализует информацию исходного признакового пространства F. Такой подход получил название метод главных компонент (PCA – principal component analysis), который активно используется в практике машинного обучения.

Так получилось, что этот алгоритм в прошлом переоткрывали несколько раз в разных прикладных областях. В результате, у него сформировалось множество разных названий. Например, я впервые о нем узнал, как о преобразовании Карунена-Лоэва, когда работал над кандидатской диссертацией. Есть и другие названия, но все это об одном и том же.

Чтобы не перегружать вас информацией, я расскажу на следующем занятии, как с помощью метода главных компонент можно сокращать признаковое пространство и устранять проблему мультиколлинеарности признаков, которая является причиной переобучения моделей.

Практический курс по ML: https://stepik.org/course/209247/

Метод главных компонент (Principal Component Analysis)

Видео по теме