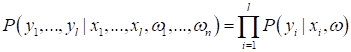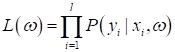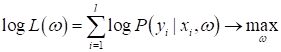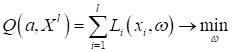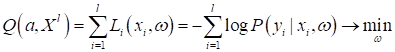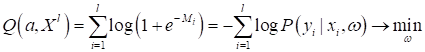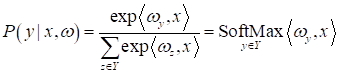Логистическая регрессия. Вероятностный взгляд на машинное обучение

Практический курс по ML: https://stepik.org/course/209247/

Давайте представим следующую задачу бинарной классификации. Пусть некий банк выдает кредиты заемщикам. Для этого он требует следующие сведения (помимо персональных данных):

Смотрите, что здесь получается. Для одинаковых объектов (наблюдений) целевое значение может меняться: кредит иногда возвращают, а иногда нет. То есть, у нас должна быть параметрическая модель, например, линейная:

которая для одного и того же вектора  иногда возвращает 1, а иногда -1. Но детерминированная модель (без случайностей) не обладает таким свойством. Мы будет иметь либо все время 1, либо все время -1. Как быть в такой ситуации? Разрешить ее можно очень просто. Почему бы нам возвращать не номер класса 1 или -1, а вероятность появления прогнозируемого класса. И, так как мы здесь переходим к вероятностям, то давайте использовать вероятностный подход для описания данной задачи:

Данная условная вероятность показывает вероятность появления прогнозируемого класса моделью  при предъявлении конкретного объекта  и вектора весов . Например, согласно приведенной таблицы, для объекта:

вероятность:

А противоположную вероятность (для класса -1), можно вычислить как:

Фактически, наша модель должна выдавать вещественное число в диапазоне [0;1]:

и это, в некотором смысле, роднит ее с задачей регрессии.

Чтобы решить поставленную задачу, нам нужно понять, как вычислять вектор весов . И, так как у нас вероятностная постановка задачи, то этот вектор будем искать, опираясь на выражение вероятности . Для этого в машинном обучении пользуются методом максимального правдоподобия:

То есть, мы выбираем такое , при котором вероятность достигает максимального значения.

Если вы не знакомы с методом максимального правдоподобия, то советую посмотреть занятие, посвященное этой теме:

https://www.youtube.com/watch?v=hO-pATDf75k

Однако, у нас с вами не одно какое-то наблюдение, а целая обучающая выборка, которая описывается, в общем случае, многомерной величиной:

Но для задачи оптимизации нам нужно как-то конкретизировать это выражение. И вот здесь, в машинном обучении, делают довольно сильное предположение: пусть все объекты  обучающей выборки независимы между собой. Тогда эту многомерную формулу можно представить, как произведение отдельных вероятностей:

Такое упрощение многомерного распределения соответствует задаче, известной под названием наивный байесовский классификатор (Naive Bayes classifier).

Причем, в эту формулу мы подставляем конкретные значения  и , а менять (подбирать) можем только вектор коэффициентов . Следовательно, она представляет собой функцию, зависящую только от этого вектора:

Такая функция получила название функции правдоподобия и для поиска наилучших значений вектора  по всей обучающей выборке, мы должны ее максимизировать:

Но искать максимум от произведения величин не очень удобно. Поэтому часто переходят к логарифму правдоподобия (log-likelihood, log-loss):

Мы всегда можем это делать, так как функция логарифма монотонно-возрастающая, а значит, никак не влияет на положение точки максимума функции.

А теперь смотрите, ранее при решении задач классификации, мы с вами вводили функционал, аппроксимирующий эмпирический риск некоторой выбранной функцией потерь:

Видите сходство этих двух критериев качества? Только в одном случае мы максимизируем, а в другом – минимизируем. Но это легко свести к единой задаче минимизации и записать следующее равенство:

Отсюда следует важный, ключевой вывод: вероятностный взгляд на задачи машинного обучения и взгляд через определение моделей с функциями потерь – это, фактически, одно и то же. Мы совершенно спокойно можем переходить из модельной плоскости в вероятностную и обратно при решении любых задач машинного обучения.

Если теперь в качестве функции потерь выбрать логарифмическую:

чтобы сходство обеих сумм было еще больше. Я напомню, что

отступ для i-го образца, показывающий, насколько далеко он находится от разделяющей гиперплоскости. Для корректного вычисления отступа для обоих классов, целевые выходы должны быть . Также из формулы отступа автоматически вытекает линейная формула для определения разделяющей гиперплоскости:

В результате, мы имеем:

Откуда следует, что:

или в виде:

То есть, логарифмическая функция потерь приводит нас к достаточно простой формуле построения оценок вероятностей для прогнозируемого класса. Причем, функция:

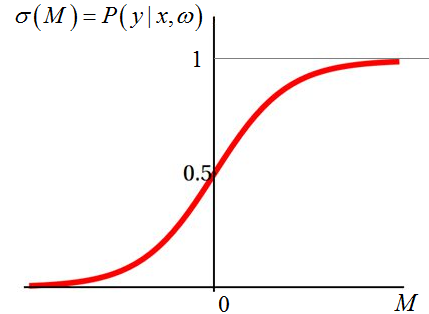
называется сигмоидальной и непосредственно связана с логарифмической (логистической) функцией потерь. Отсюда и пошло название такого класса задач – логистическая регрессия.

График сигмоиды выглядит, следующим образом:

И из него хорошо видно, что чем дальше от разделяющей гиперплоскости находится правильно спрогнозированный класс (M > 0), тем выше значение вероятности (уверенности) классификатора, что прогноз верен. И, наоборот, если знак отступа отрицательный (M < 0), значит, произошла ошибка классификации и вероятность будет меньше 0,5. Если же образ оказался точно на разделяющей гиперплоскости, то на выходе увидим значение 0,5, то есть, классификатор не уверен, к какому классу отнести текущий вектор .

Многоклассовая логистическая регрессия

В заключение этого занятия скажу несколько слов про многоклассовую логистическую регрессию. Она используется, когда решается задача M-классовой классификации, причем образы не пересекаются. В этом случае для каждого класса  имеется свой вектор весовых коэффициентов  и мы выбираем тот класс, для которого скалярное произведение:

наибольшее. Затем, для вычисления вероятности правильного выбора, можно воспользоваться следующей формулой:

которая носит название функции softmax. Она довольно часто используется на практике, в частности в нейронных сетях, когда входной вектор нужно отнести к одному из M классов. Тогда на выходе сети прописывают функцию softmax и получают некий аналог вероятностей отнесения объекта к тому или иному классу.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation