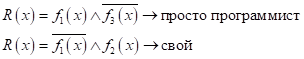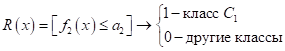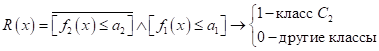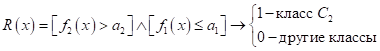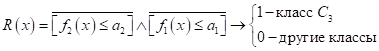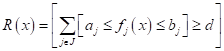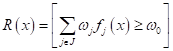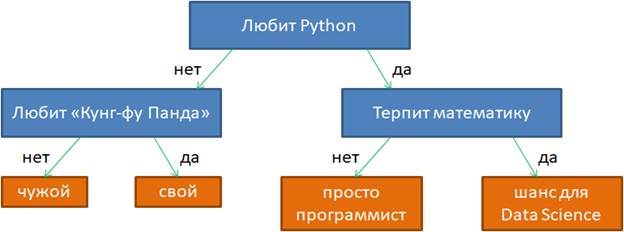
Логические методы классификации

Практический курс по ML: https://stepik.org/course/209247/

На этом занятии мы затронем новый класс алгоритмов в машинном обучении под названием логические методы классификации. В чем суть таких методов? Смотрите. Довольно часто на практике встречаются задачи, где требуется делать вывод по небольшому набору исходных данных (признаков), выстраивая некоторую цепочку рассуждений. Например, следующая схема позволяет сделать некоторые выводы в зависимости от пары ответов на простые вопросы:

Здесь условно можно выделить три бинарных признака:

И сформировать на их основе логические правила вывода, например:

То есть, в каждом правиле мы имеем последовательность утверждений, которые все должны быть выполнены, чтобы сделать тот или иной вывод. Это простейшие примеры логических выводов на основе серии конъюнкций бинарных признаков. Причем в логических правилах используется довольно ограниченное число признаков для вывода (рекомендуется 2-4 и не более 7). Это связано с человеческим восприятием такого вывода, когда эксперт пытается понять, почему алгоритм рекомендует то или иное решение. Осознать два-три признака (предиката) относительно просто. Например, система отклоняет кредит заемщику, отмечая, что у него низкий доход и большой возраст. А если этих показателей будет больше, например, наличие квартиры, детей, машины, загран паспорта и т.п., то эксперту уже значительно сложнее оценить причины отказа или, наоборот, рекомендации выдать кредит. И так в самых разных областях. Поэтому рекомендательные системы и в целом логические методы, как правило, оперируют небольшим числом признаков.

Хорошо, я думаю этот момент понятен. Давайте теперь несколько расширим, обобщим правила логических выводов, положим признаки вещественными, числовыми:

Здесь n – общее число признаков, вычисленных по вектору . Как в таком случае строить логические выводы? Очевидно, здесь каждый признак нужно сравнивать с некоторым числовым порогом и выдавать ответы 0 или 1 (аналог «да» и «нет»). Математически это удобно записать с использованием нотации Айверсона:

или в еще более общей форме:

Если условие выполняется, то скобка возвращает 1, иначе – 0. В результате мы превращаем вещественный признак снова в бинарный и можем формировать логические правила по ранее приведенному принципу:

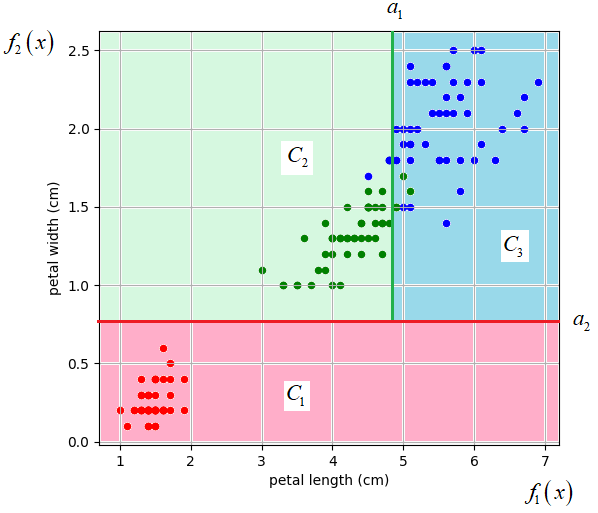
Здесь J – это множество признаков, которые мы отбираем для формирования вывода.

Чтобы эта математика была более понятна, приведу пример с классификацией цветов ириса Фишера. На рисунке тремя разными цветами показано распределение трех видов цветков ирисов по двум признакам: ширина и длина лепестков. Наша цель – разделить их по классам, используя правила логического вывода на основе этих двух вещественных признаков.

Очевидно, первый класс  (красные точки) очень хорошо отделяется от других по второму признаку с отсечением по порогу :

Для классификации двух других дополнительно нужно сравнивать первый признак с порогом :

Здесь верхняя черта означает отрицание предиката (если было 0, становится 1, если была 1, становится 0). Или, этот же логический вывод можно записать без отрицания, изменив только знак в скобке на больше:

Очевидно, получим то же самое правило.

Наконец, последний третий класс можно выделить по правилу:

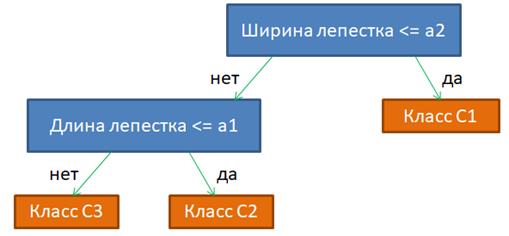
Вот пример с вещественными признаками и набором правил логического вывода для определения видов цветов ириса. Все эти правила можно объединить и построить следующее решающее дерево:

Я не случайно назвал этот направленный ациклический граф решающим деревом. Это один из самых распространенных подходов среди логических методов классификации. То есть, если на основе исходных размеченных данных (обучающей выборки) удается построить такую древовидную структуру, то у нас автоматически формируется набор правил для классификации данных обучающей выборки. А если повезет, то и для произвольных данных той же природы, что и обучающая выборка.

Но прежде чем с головой погрузиться в теорию решающих деревьев, следует отметить, что логические методы не ограничиваются только ими. Есть еще несколько общих подходов для формирования правил логического вывода.

С первым общим подходом мы с вами только что познакомились – это набор предикатов, объединенных конъюнкциями:

и, как следствие, получаем из них решающие деревья. Другой подход под названием синдром был подсмотрен во врачебной практике (отсюда и его название). Когда врач ставит диагноз, то вначале изучает набор симптомов у пациента, а затем, делает вывод в пользу заболевания, которому в большей степени соответствуют наблюдаемые симптомы. Математически это можно формализовать, так:

То есть, здесь мы имеем определенный набор признаков (измерений) J. Например, температура тела, покраснение, першение в горле и т.п. А, затем, подсчитываем, сколько из этих признаков не соответствуют норме, то есть, выделяем набор симптомов. Причем, у разных пациентов набор этих симптомов может быть разным. Но если набирается определенное количество d симптомов характерных для той или иной болезни, то делается вывод (ставится диагноз), что у больного именно это заболевание.

Наконец, есть еще пара известных, но менее распространенных схем построения логических выводов:

- полуплоскость (линейная пороговая функция):

- шар (пороговая функция близости):

Здесь  - некоторая метрика (расстояние между векторами). В последнем случае мы смотрим, насколько близок вектор  к некоторому характерному представителю  определенного класса. Если  попадает в окрестность  по совокупности определенных признаков, то мы относим его к тому же классу, что и .

Подобных правил огромное количество, но остальные очень редко используются на практике. В основном, самые простые, что мы отметили в начале нашего занятия.

У вас здесь может возникнуть вопрос, а какие правила, когда использовать? В действительности, это часто следует из постановки задачи (технического задания – ТЗ). Некоторые эксперты хорошо воспринимают правила в виде набора конъюнкций. Другие (в частности, медики) – правила на основе синдромов. Где-то явно следует выделять характерные объекты и измерять близость до них. И так далее. То есть, все это, как правило, следует из самой решаемой задачи. Но чаще всего, все же, используются правила в виде набора конъюнкций, которые хорошо выражаются в виде решающих деревьев. Именно о них мы подробнее поговорим на следующем занятии.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation