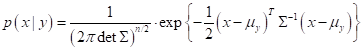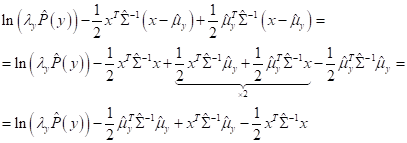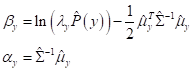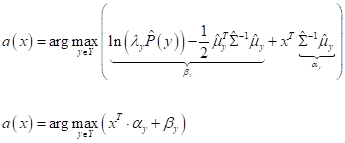Линейный дискриминант ФишераПрактический курс по ML: https://stepik.org/course/209247/ Довольно интересным частным случаем гауссовского байесовского классификатора, который мы рассмотрели на предыдущем занятии, является линейный дискриминант Фишера. Он строится исходя из предположения о равенстве всех ковариационных матриц классов:
Я напомню, что модель строится по правилу:
где
в случае
гауссового распределения признаков вектора Так вот, при равенстве всех ковариационных матриц разных классов, нам достаточно оценить векторы математических ожиданий (МО):
и общую ковариационную матрицу уже по всем объектам обучающей выборки:
То есть, у нас МО разные (свои) для каждого класса, а ковариационная матрица общая. В итоге, классификатор принимает вид (с использованием логарифмической функции):
Обратите
внимание, мы здесь убрали слагаемое Далее, выражение под argmax можно расписать, следующим образом:
Последнее
слагаемое
Если теперь для
каждого класса
то классификатор примет вид:
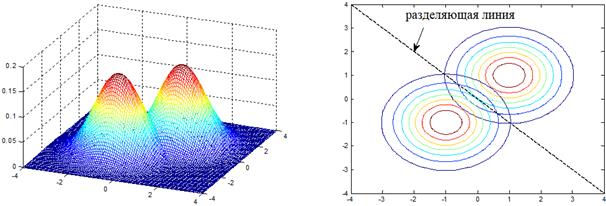
Это вам ничего не напоминает? Да, это обычный линейный классификатор, о котором мы с вами ранее уже говорили. Он получил название линейный дискриминант Фишера. В честь ученого, который впервые решил эту задачу в далеком 1936 году. Получается, если распределение множества объектов разных классов подчиняются гауссовскому закону и имеют одинаковые ковариационные матрицы, то оптимальный классификатор для них будет линейным (или кусочно-линейным для множества классов). И это понятно. Если мы посмотрим на границу пересечения двух нормальных двумерных ПРВ с одинаковыми ковариационными матрицами, то увидим, что линия с равными вероятностями классов будет линейной:
Даже если мы будем выбирать разные штрафы, или классы будут иметь разные априорные вероятности, то эта линия просто будет смещаться вправо или влево – в сторону от класса с большим штрафом и/или большей априорной вероятностью. Форма же разделяющей линии или гиперплоскости будет оставаться неизменной. Поэтому алгоритм классификации при таких исходных данных всегда линеен. Основным преимуществом линейного дискриминанта Фишера в простоте его реализации (малого объема вычислений) и, кроме того, возможность вычислять ковариационную матрицу по всем объектам выборки, а не по объектам одного отдельного класса. Этот подход помогает, когда выборка сильно не сбалансирована и представителей отдельного класса может быть недостаточно для хорошей оценки ковариационной матрицы. В дискриминанте Фишера такой проблемы, как правило, нет. Однако, и в
гауссовском байесовском классификаторе и в линейном дискриминанте Фишера
остается одна главная проблема с обращением матрицы ковариаций Во втором способе добавляют к элементам главной диагонали ковариационной матрицы небольшие ненулевые значения:
где
Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
- штрафы за
неверную классификацию класса 
;
- априорная
вероятность появления класса 
.
,
которое присутствует в гауссовском байесовском классификаторе, т.к. при
равенстве ковариационных матриц, эта величина одна и та же для всех классов, а
значит, ее можно отбросить.
не зависит от
номера класса, следовательно, его можно также не учитывать. Получаем
классификатор в виде:
. Как вы уже
знаете, из-за линейных или почти линейных зависимостей между признаками эта
матрица становится плохо обусловленной и обратная матрица может даже не
существовать. Решить эту проблему можно двумя распространенными способами. Один
мы с вами совсем недавно уже рассмотрели – это считать все признаки
независимыми, тогда матрица ковариаций вырождается в диагональную матрицу,
которая всегда хорошо обращается. В итоге, мы приходим к наивному байесовскому
классификатору.
,
- небольшое
значение; 
- единичная
матрица. Этот подход соответствует L2-регуляризации и, конечно же, в
байесовских классификаторах его также можно использовать.
