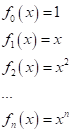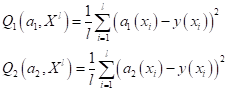Практический курс по ML: https://stepik.org/course/209247/
На предыдущем
занятии мы увидели, что задачи машинного обучения – это задачи оптимизации, в
частности минимизации эмпирического риска:
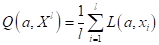
зависящего, в
общем виде, от модели 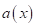 и
вида функции потерь
и
вида функции потерь 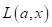 .
То есть, нам нужно выбрать такую модель, чтобы функционал принимал наименьшее
значение на обучающей выборке. Математически это можно записать так:
.
То есть, нам нужно выбрать такую модель, чтобы функционал принимал наименьшее
значение на обучающей выборке. Математически это можно записать так:
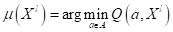
Здесь 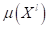 - найденная
модель на этапе обучения по всем возможным моделям
- найденная
модель на этапе обучения по всем возможным моделям 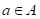 ; argmin – определяет
значение аргумента, при котором функция принимает наименьшее значение.
; argmin – определяет
значение аргумента, при котором функция принимает наименьшее значение.
В случае
параметрических моделей 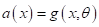 это
выражение может быть записано относительно вектора параметров
это
выражение может быть записано относительно вектора параметров 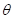 :
:
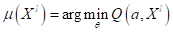
После обучения
мы принимаем 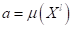 и
используем найденную зависимость в продакшене (при практической реализации).
и
используем найденную зависимость в продакшене (при практической реализации).
Вот так
математически можно кратко записать то, о чем мы говорили на предыдущем
занятии. Давайте снова вернемся к нашему простейшему примеру – методу
наименьших квадратов. Здесь у нас данные формируются по закону:
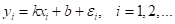
где 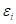 - по
прежнему гауссовский шум с нулевым средним. Для такой задачи оптимальная модель
имеет вид линейной функции:
- по
прежнему гауссовский шум с нулевым средним. Для такой задачи оптимальная модель
имеет вид линейной функции:
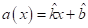
Неизвестные
параметры 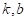 я
обозначил с крышечкой, что означает, что мы не можем их точно определить
(всегда будет погрешность, неточность). Так вот, эту же модель можно записать и
в таком виде:
я
обозначил с крышечкой, что означает, что мы не можем их точно определить
(всегда будет погрешность, неточность). Так вот, эту же модель можно записать и
в таком виде:
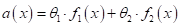
если выбрать: 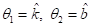 и
и 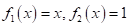 . Модели,
которые представляют собой линейную комбинацию признаков с некоторыми
настраиваемыми параметрами (весами), называются линейными.
. Модели,
которые представляют собой линейную комбинацию признаков с некоторыми
настраиваемыми параметрами (весами), называются линейными.
В общем случае
любую линейную модель можно представить в виде следующей суммы:
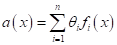
Почему такая
модель считается линейной? Если мы перейдем в пространство признаков 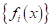 , то
в нем модель
, то
в нем модель 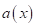 будет
описывать гиперплоскость, ориентация которой определяется вектором параметров
будет
описывать гиперплоскость, ориентация которой определяется вектором параметров 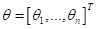 :
:
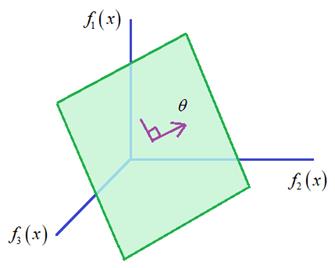
Такие модели
достаточно просты, хорошо изучены и нередко приводят к приемлемым результатам. Мы
с вами вначале подробно изучим работу этих моделей.
Давайте для примера
рассмотрим задачу линейной регрессии, в которой будем строить аппроксимацию
эмпирических данных, сформированных по правилу:
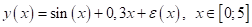
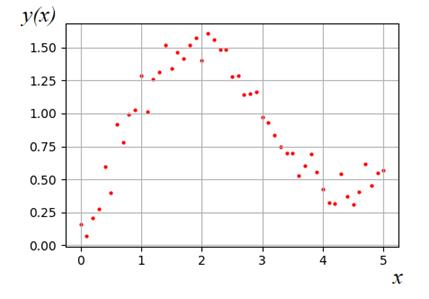
Строго говоря,
мы здесь имеем одномерную величину 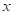 , по
которой нужно спрогнозировать выходное значение
, по
которой нужно спрогнозировать выходное значение 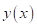 . То
есть, исходные измерения – это
. То
есть, исходные измерения – это 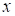 , а целевые
выходные – это
, а целевые
выходные – это 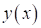 .
Однако, если строить линейную модель по одному признаку
.
Однако, если строить линейную модель по одному признаку 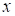 в
виде:
в
виде:
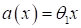
то, как вы
понимаете, мы очень грубо будем описывать изменения представленных (на графике)
точек. Здесь явно нелинейная зависимость 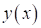 .
Поэтому, чтобы оставаться в рамках линейной модели при решении подобных задач,
мы расширим признаковое пространство следующими преобразованиями:
.
Поэтому, чтобы оставаться в рамках линейной модели при решении подобных задач,
мы расширим признаковое пространство следующими преобразованиями:
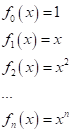
Причем,
преобразования, как правило, выбираются так, чтобы признаки были линейно
независимыми. Иначе, один признак просто сведется к другому. Например, пара
преобразований:
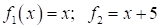
это, фактически,
один и тот же признак, т.к. значение +5 с успехом может быть добавлено
признаком
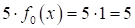
Вот на это
следует обращать внимание при формировании нового признакового пространства –
оно должно быть информативным, а не просто дублировать данные.
Итак, расширение
пространства признаков с помощью функциональных преобразований – это нормальная
практика. В результате, наша линейная модель будет вычислять выходные значения
в виде полинома:
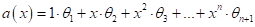
где 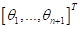 - вектор
весовых коэффициентов, которые определяются по входным эмпирическим данным
(обучающей выборке). То есть, для каждого
- вектор
весовых коэффициентов, которые определяются по входным эмпирическим данным
(обучающей выборке). То есть, для каждого 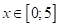 мы
будем вычислять
мы
будем вычислять 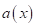 -
это и будет прогнозом величины
-
это и будет прогнозом величины  . В
результате, если взять полином первой степени (
. В
результате, если взять полином первой степени (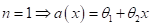 ),
то получим аппроксимацию точек линейной функцией:
),
то получим аппроксимацию точек линейной функцией:
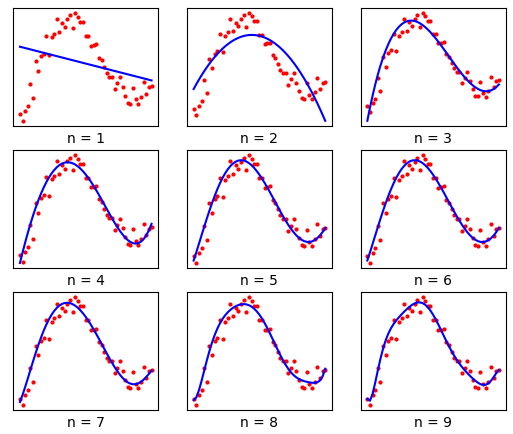
Увеличивая
порядок полинома, мы все точнее и точнее будем описывать экспериментальные
зависимости. Казалось бы, мы с вами только что нашли универсальное решения для
задачи регрессии (да и классификацию тоже можно делать по этому принципу)?
Берем полином сколь угодно большой степени и описываем им эмпирические данные с
нужной точностью. Но, увы, природа так просто не сдает своих позиций и в
полиномах с высокими степенями кроется один неприятный момент. Давайте возьмем
функцию вида:
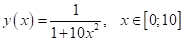
И будем ее
приближать полиномом степени n = 54. Но коэффициенты полинома будем
вычислять только по половине всех точек, взятых через отсчет. Тогда в другой
половине точек полученная модель
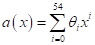
будет строить
прогноз.
На рисунке ниже
красными точками показаны значения функции, участвующие в расчетах параметров 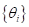 , а
зелеными – точки, в которых строится прогноз по полученной модели.
, а
зелеными – точки, в которых строится прогноз по полученной модели.
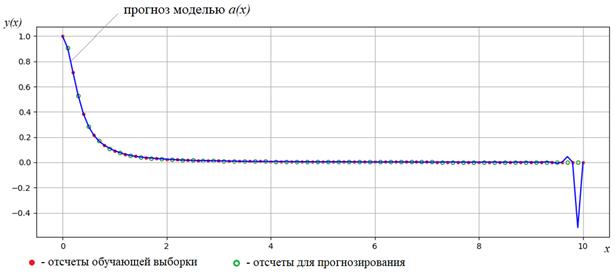
Как видите, при
больших значениях 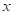 полином
ведет себя совершенно непредсказуемым образом. Это известный факт, знакомый
всем математикам. Применительно к нашей задаче, это означает, что такая модель плохо
будет строить прогнозы в новых, неизвестных ей точках. То есть, с одной
стороны, полином высокой степени хорошо описывает точки обучающей выборки, но
совершенно непригоден для построения прогнозов в новых точках.
полином
ведет себя совершенно непредсказуемым образом. Это известный факт, знакомый
всем математикам. Применительно к нашей задаче, это означает, что такая модель плохо
будет строить прогнозы в новых, неизвестных ей точках. То есть, с одной
стороны, полином высокой степени хорошо описывает точки обучающей выборки, но
совершенно непригоден для построения прогнозов в новых точках.
А вот с
полиномами меньших степеней таких проблем, как правило, нет. Я приведу еще один
график, где покажу, как меняется значение эмпирического риска для двух моделей:
-
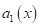 - вычисленная
по всем точкам функции
- вычисленная
по всем точкам функции 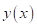 ;
;
-
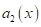 -
вычисленная по половине точек, взятых через отсчет.
-
вычисленная по половине точек, взятых через отсчет.
В результате,
имеем два выражения для эмпирических рисков:
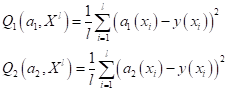
и их графики при
разных степенях полиномов 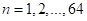 :
:
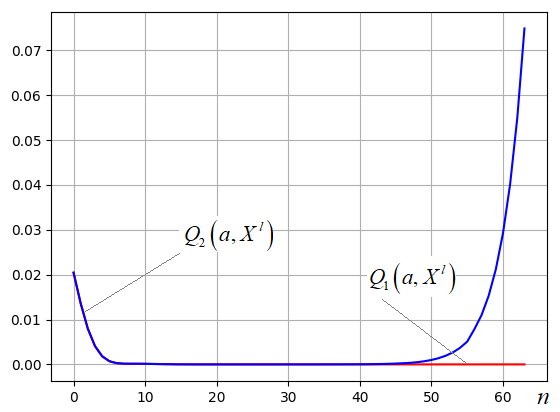
Здесь синий
график – это 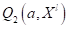 , а
красный -
, а
красный - 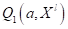 . Хорошо
видно, что сначала увеличение степени полиномов приводит к улучшению степени
аппроксимации функции, а затем, при больших степенях синий график резко
возрастает и расходится с красным. Это, как раз, связано с непредсказуемостью
поведения полиномов с большими степенями и ухудшением их предсказательной
способности.
. Хорошо
видно, что сначала увеличение степени полиномов приводит к улучшению степени
аппроксимации функции, а затем, при больших степенях синий график резко
возрастает и расходится с красным. Это, как раз, связано с непредсказуемостью
поведения полиномов с большими степенями и ухудшением их предсказательной
способности.
С точки зрения машинного
обучения – это яркий пример эффекта переобучения (overfitting). То есть,
переобучение – это несоответствие найденной модели 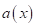 закону
изменения данных, часть которых была представлена в обучающей выборке. При этом
данные самой обучающей выборки описываются моделью хорошо. В результате, такая
переобученная модель не обладает достаточными обобщающими способностями – ее
нельзя расширить на произвольный набор данных
закону
изменения данных, часть которых была представлена в обучающей выборке. При этом
данные самой обучающей выборки описываются моделью хорошо. В результате, такая
переобученная модель не обладает достаточными обобщающими способностями – ее
нельзя расширить на произвольный набор данных 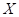 той
же природы, что и в обучающей выборке. А это именно то, что мы хотим от нашей
модели – применять ее для новых наблюдений и получать корректные результаты. То
есть, здесь важно не просто провести функцию по эмпирическим зависимостям, а
выделить их модель, закон природы. В этом и заключается главная задача
машинного обучения.
той
же природы, что и в обучающей выборке. А это именно то, что мы хотим от нашей
модели – применять ее для новых наблюдений и получать корректные результаты. То
есть, здесь важно не просто провести функцию по эмпирическим зависимостям, а
выделить их модель, закон природы. В этом и заключается главная задача
машинного обучения.
Надо сказать,
что абсолютно любая модель 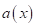 ,
найденная по эмпирическим данным, обладает то или иной степенью
переобученности. Избавиться полностью от этого эффекта невозможно, мы всегда
будем, так или иначе, подстраиваться под данные обучающей выборки. И все, что
можем сделать – это минимизировать данный эффект и, как следствие, повысить обобщающую
способность нашей модели.
,
найденная по эмпирическим данным, обладает то или иной степенью
переобученности. Избавиться полностью от этого эффекта невозможно, мы всегда
будем, так или иначе, подстраиваться под данные обучающей выборки. И все, что
можем сделать – это минимизировать данный эффект и, как следствие, повысить обобщающую
способность нашей модели.
Практический курс по ML: https://stepik.org/course/209247/