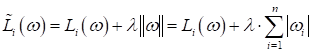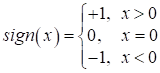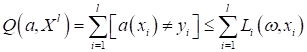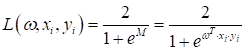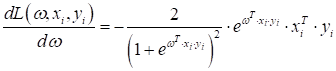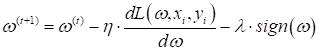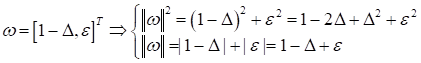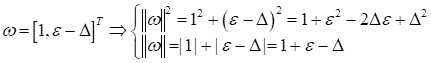|
L1-регуляризатор. Отличия между L1- и L2-регуляризаторамиПрактический курс по ML: https://stepik.org/course/209247/ На предыдущем занятии мы с вами подробно познакомились с принципом L2-регуляризации коэффициентов модели и увидели, что эта эвристика действительно позволяет заметно уменьшить переобучение модели и увеличить ее обобщающие свойства. Но раз L2-регуляризатор – это всего лишь эвристика, то почему бы не попробовать и другие подходы, например, вместо квадрата нормы вектора весовых коэффициентов:
взять модули – норму первой степени:
В машинном
обучении это называется L1-регуляризацией. Чтобы ее применить на
практике, например, в градиентных алгоритмах, нам нужно уметь вычислять
производную по функции потерь. Но, как вы знаете из курса математики, функция
где
В итоге, стохастический градиентный алгоритм (SGD) можно записать, следующим образом:
Формально,
конечно, нужно было умножить последнее слагаемое на Давайте посмотрим, как будет работать такой L1-регуляризатор в уже знакомой нам простой задаче классификации гусениц и божьих коровок. Изначально, у нас есть следующие результаты измерений:
Это обучающая выборка с двумерными входными векторами:
и целевыми ответами:
Давайте теперь расширим пространство признаков, но специально сделаем их линейно-зависимыми, например, такими:
Видите, здесь последние три признака – это линейная комбинация первых двух. То есть, они не несут в себе никакой дополнительной информации и, фактически, не нужны для данной задачи бинарной классификации жуков. Следующим шагом построим модель и определим функционал качества для обучения модели. Как всегда, выберем простой линейный классификатор вида:
который выдает -1 гусениц и +1 – для божьих коровок. А эмпирический риск:
будем минимизировать уже знакомой нам сигмоидной функцией потерь:
с производной по
Такую задачу мы с вами уже решали. Добавим сюда L1-регуляризатор и стохастический градиентный алгоритм примет вид:
Реализуем его на Python: Смотрите, если
поставить значение параметра [ 1.94650481e-05 3.18980823e-05 6.43046505e-02 -3.38310192e-02 3.46815652e-04] А если убрать
регуляризатор ( [ 0.00804764 -0.00525472 0.0804764 -0.05254715 0.01396463] Видите качественные отличия? При использовании L1-регуляризатора у нас коэффициенты при линейно-зависимых признаках стали заметно меньше и были выделены только два – ширина и длина, умноженная на 10. Почему регуляризатор выделили именно эти два, а не первые, на основе которых мы и формировали остальные? Все просто. При умножении на 10 градиенты для этой пары также увеличились и они стали доминировать над остальными. Вы можете подумать, что ослабление признаков через коэффициенты можно добиться любым регуляризатором, например L2. Давайте проверим. Для этого достаточно последнее слагаемое в производной функции потерь записать в виде:
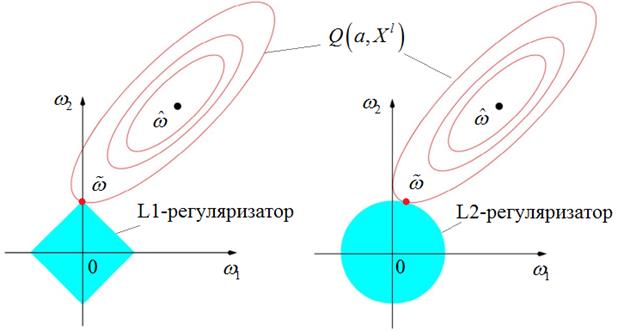
После запуска программы видим результат: [ 0.00798617 -0.00536355 0.07986168 -0.05363546 0.01311311] То есть, L2-регуляризатор лишь не дает расти коэффициентам в сложных моделях (при большом числе признаков), но не устремляет коэффициенты к нулю, как это происходит с L1-регуляризатором. Но почему эти два регуляризатора ведут себя так по-разному? Объяснить этот эффект можно несколькими способами. Первый, самый простой – графический. Давайте для
простоты рассмотрим двумерное признаковое пространство с двумя весовыми
коэффициентами
В этом
пространстве есть точка минимума К чему это
приводит, я думаю, вы уже догадались? При L1-регуляризаторе
вероятность соприкоснуться функционалу качества И, обратите внимание, применение L1-регуляризатора не гарантирует обнуление всех не значимых признаков. Этот эффект проявляется лишь с некоторой большой вероятностью. Но вполне может так получиться, что точка пересечения областей придется на грань ромба и некоторые признаки не устремятся к нулю, даже если будут линейно-зависимыми. Второе объяснение различия в поведении L1 и L2-регуляризаторов можно дать чисто математически. Давайте предположим, что наш двумерный вектор весовых коэффициентов имеет, следующие значения:
где
Вначале будем менять первую координату:
При изменении второй координаты:
Смотрите, когда
мы уменьшаем большее значение Я думаю этих двух объяснений вполне достаточно, чтобы понять отличия в поведении этих двух регуляризаторов. Если вам все же этого недостаточно, то в литературе можно найти и другие объяснения особенностей работы L1 и L2-регуляризаторов. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
не
имеет производной в точке 
.
Поэтому найти оптимальные коэффициенты аналитически у нас не получится. В этом
случае применяют численные методы, например, градиентный спуск. Градиент
функции потерь с L1-регуляризатором будет иметь вид:
,
, но я просто
переобозначил параметр 
.
,
равной:
,
то коэффициенты принимают значения:
),
то получим уже такой вектор весовых коэффициентов:
:
функционала
и
когда мы работаем без регуляризаторов, то именно ее и стараемся обнаружить. Но,
добавляя регуляризацию, возникает дополнительное условие со множеством точек,
удовлетворяющих L1-регуляризатору, в виде ромба, и множеством точек
для L2-регуляризатора
виде круга. Так вот, суммируя первую область для 
,
находящейся на пересечении кривых уровня этих двух составляющих. И градиентный
алгоритм устремляется к этой новой точке.
,
.
И затем проанализируем, как будут меняться квадрат нормы 
и
единичная норма 
вектора
:
,
то квадратичная норма уменьшается быстрее, чем при изменении малого второго
значения 
.
А в случае с единичной нормы – без разницы какое из значений уменьшать. В обоих
случаях она будет меняться на одну и ту же величину. Из этого следует, что при
использовании L2-регуляризаторов
предпочтение будет отдаваться уменьшению больших величин, а при использовании L1-регуляризаторов
– все значения вектора 
