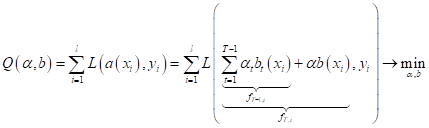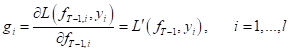Градиентный бустинг и стохастический градиентный бустинг

Практический курс по ML: https://stepik.org/course/209247/

На предыдущих занятиях мы с вами разобрались в принципе бустинга простых алгоритмов – формирования их композиции для задач регрессии и классификации:

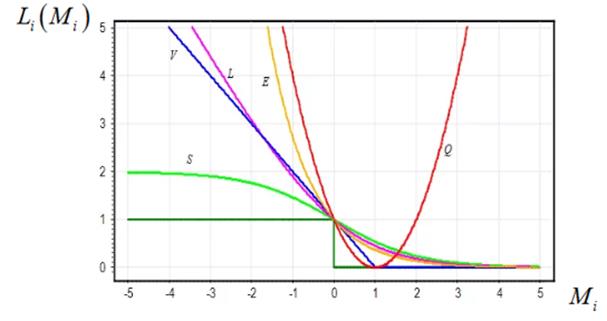
При этом, мы увидели, что в разных задачах используются разные функции потерь в функционале качества композиции:

по обучающей выборке . Так, в задаче бинарной классификации алгоритм AdaBoost использует экспоненциальную функцию потерь, а в задаче регрессии – квадратичную. Другие функции потерь позволяют получать другие известные алгоритмы бустинга:

•  - экспоненциальная (AdaBoost);
•  - логарифмическая (LogitBoost);
•  - квадратичная (GentleBoost);
•  - гауссовская (BrownBoost).

И так далее. Можно придумать много других функций для разработки (синтеза) новых алгоритмов бустинга. И здесь возникает естественный вопрос. А можно ли создать универсальный алгоритм бустинга, который бы работал с произвольной гладкой и дифференцируемой функцией потерь? Оказывается да, можно и такой подход получил название градиентного бустинга.

Впервые градиентный бустинг представил Jerome Friedman (Джером Фридман) в 1999 году. Эта идея оказалась настолько продуктивной, что градиентный бустинг стал одним из стандартных инструментов для попыток решить ту или иную задачу машинного обучения. В частности, знаменитый Матрикснет от компании Яндекс использует его над небрежными решающими деревьями (ODT) при ранжировании поисковой выдачи. И, как видите, это работает вполне неплохо.

Давайте вначале разберемся в принципах работы градиентного бустинга. Я взял фрагмент его вывода из лекций профессора Воронцова, как наиболее простой и понятный.

Итак, все начинается с построения взвешенной композиции алгоритмов:

и выбора функционала качества для поиска весов  и конкретных алгоритмов . Мы его запишем в общем виде через некоторую функцию потерь :

Я здесь сразу расписал композицию через T-1 уже известных алгоритмов (найденных на предыдущих T-1 шагах) и текущего  с некоторым (пока еще неизвестным) весом . Мы должны найти эти два элемента из условия минимума функционала . Еще раз напомню, что здесь реализуется «жадная» стратегия поиска алгоритмов: все ранее найденные алгоритмы  и весовые коэффициенты  фиксируются и больше не меняются.

Выходы композиции по T-1 алгоритмам для каждого образа  обучающей выборки мы обозначим через вектор:

А выходы по всем T алгоритмам – через вектор:

Тогда смотрите, что получается. На следующем шаге T мы должны выбрать такой вектор , который бы уменьшал значение функционала качества  по сравнению с предыдущим вектором . Вам это ничего не напоминает? Это, фактически, описание работы градиентного алгоритма. Если вычислить градиент функции потерь:

то корректировку i-го компонента можно записать, следующим образом:

А у нас в формуле (согласно композиции алгоритмов) эта же самая корректировка выглядит, как:

Сходство очевидно. И, так как, коэффициент , то алгоритм  на текущем шаге T должен выдавать значения как можно ближе к антиградиенту функции потерь:

Здесь используется квадратическая функция, как мера близости i-х значений и суммируется все по обучающей выборке. Почему именно квадратическая функция? Потому что она, в ряде случаев, позволяет аналитически найти решение по методу наименьших квадратов (МНК). Мало того, решающие деревья для задач регрессии часто по умолчанию используют именно этот критерий.

Итак, мы довольно просто можем найти наилучший алгоритм  на шаге T, зная градиент функции потерь и решая задачу наименьших квадратов. Это отработанная математическая практика и ничего сложного здесь нет. И нам осталось последнее – вычислить (найти) весовой коэффициент . Так как мы рассматриваем общую задачу с произвольной функцией потерь, то поиск этого весового коэффициента сводится к следующей задаче одномерной оптимизации:

Ее можно достаточно быстро (в вычислительном плане) решить численными методами. Современные методы оптимизации с этим легко справляются (например, метод половинного деления).

Все, мы только что с вами разобрали принцип работы градиентного бустинга. И чтобы было все понятнее, приведу его псевдокод:

Вход: обучающая выборка  и параметр T (число алгоритмов в композиции)

Выход: набор базовых алгоритмов  и весов

1: начальная инициализация:

2: для всех

3:     найти наилучший текущий алгоритм, приближающий антиградиент:

4:     нахождение весового коэффициента:

5:     обновление вектора значений на объектах выборки:

Фактически, это универсальная обертка над множеством выбранного семейства базовых алгоритмов и функции потерь. На выходе получаем композицию алгоритмов, найденных по конкретной обучающей выборке. Часто в качестве семейства базовых алгоритмов выбирают решающие деревья. Из них получаются хорошие композиции, способные конкурировать с лучшими алгоритмами машинного обучения.

Стохастический градиентный бустинг

В алгоритмах градиентного бустинга, что мы рассматривали, предполагалось использование всей обучающей выборки для вычисления весов и определения алгоритмов. Но что делать, если выборка очень большая и избыточная? Тогда объем вычислений также может стать очень большим. Джером Фридман в том же 1999 году предложил очень простое решение. Давайте на каждой t-й итерации формировать выборку меньшей длины из случайно выбранных объектов исходной обучающей выборки. И оказалось, что это может приводить даже к лучшим результатам, чем использование каждый раз всей выборки. В частности было замечено:

• лучшее качество работы всей композиции;
• повышение скорости сходимости (каждый последующий алгоритм заметно улучшал качество композиции);
• уменьшение времени обучения.

Такой подход (с использованием случайных выборок) стали называть стохастическим градиентным бустингом (Stochastic Gradient Boosting – SGB).

Реализация градиентного бустинга на Python

На языке Python очень легко реализовывать различные алгоритмы бустинга. Начиная с простого AdaBoost и заканчивая продвинутым градиентным бустингом XGBoost (быстрый алгоритм градиентного бустинга над решающими деревьями). Для этого имеются следующие классы библиотеки Scikit-Learn:

• AdaBoostRegressor – AdaBoost для задач регрессии;
• AdaBoostClassifier – AdaBoost для задач классификации;
• GradientBoostingRegressor – градиентный бустинг для задач регрессии;
• GradientBosstingClassifier – градиентный бустинг для задач классификации.

А для использования XGBoost следует установить дополнительную библиотеку:

pip install xgboost

Подробную информацию можно посмотреть на странице официальной документации:

https://xgboost.readthedocs.io/en/stable/

По умолчанию все представленные алгоритмы бустинга использую решающие деревья для формирования композиции. И, скорее всего, вам не придется менять этот базовый функционал, т.к. деревья, как я уже отмечал, используются в 99% при бустинге.

Вот, что в целом из себя представляет бустинг простых алгоритмов и как его можно обобщить на произвольные функции потерь с помощью градиентного бустинга.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation