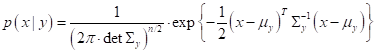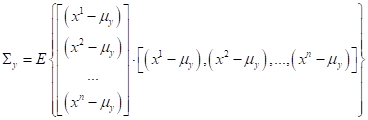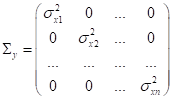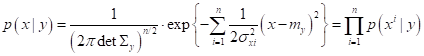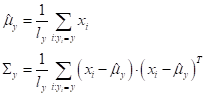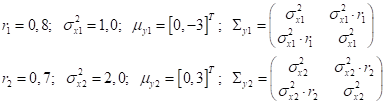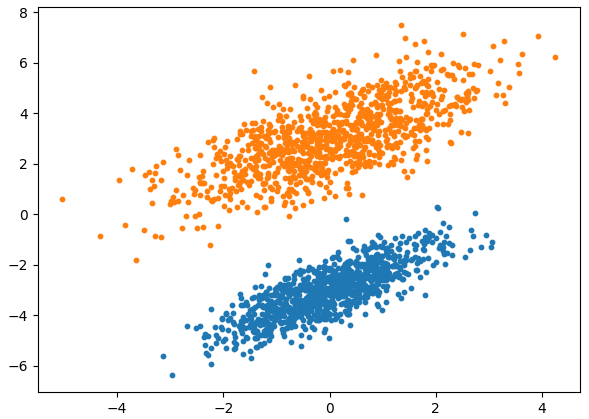
|
Гауссовский байесовский классификаторПрактический курс по ML: https://stepik.org/course/209247/ Давайте представим, что множество объектов обучающей выборки подчиняется гауссовскому (нормальному) закону распределения:
Тогда, в соответствии с теоремой Байеса, алгоритмы машинного вывода следует строить, исходя из формулы:
Здесь Так как мы полагаем, что данные выборки подчиняются гауссовскому распределению, то, формально:
Здесь
где Алгоритм принятия решения (классификации) для многомерной гауссовской ПРВ записывается также, как и для оптимального байесовского классификатора:
Напомню, что
здесь Например, когда мы рассматривали задачу наивного байесовского вывода, то полагали, что ковариационная матрица диагональная с дисперсиями по главной диагонали:
Для гауссовского распределения это автоматически означает независимость случайных величин (в данном случае независимость признаков):
Но, как вы понимаете, это очень сильное предположение, граничащее с наивностью (отсюда и название). Признаки в задачах машинного обучения довольно часто оказываются в некоторой степени линейно зависимыми. И, как мы знаем из теории вероятностей, степень линейной зависимости двух любых случайных величин определяется ковариацией:
или, нормированным коэффициентом – корреляцией:
Если значение коэффициента корреляции равно нулю, то для гауссовских случайных величин это означает полную независимость, а для остальных распределений – линейную независимость. Если же коэффициент корреляции равен 1 или -1, то СВ полностью линейно зависимы и одну величину можно вычислить по другой. В большинстве практических задач коэффициент корреляции по модулю лежит между нулем и единицей, то есть, величины линейно независимы, но лишь в некоторой степени. В этом случае применение наивного байесовского классификатора может быть под вопросом, особенно, если коэффициенты корреляции по модулю близки к единице.
Хорошо, но тогда спрашивается, как мы можем на практике учесть ковариационные связи между признаками и построить не наивный, а полноценный байесовский классификатор? Хорошая новость, что в случае многомерного гауссовского распределения это сделать относительно просто. Как вы уже догадались, для этого нам достаточно по обучающей выборке построить оценки МО и ковариационных матриц отдельно для каждого класса:
Формулы для вычисления этих оценок просты и, в целом, очевидны:
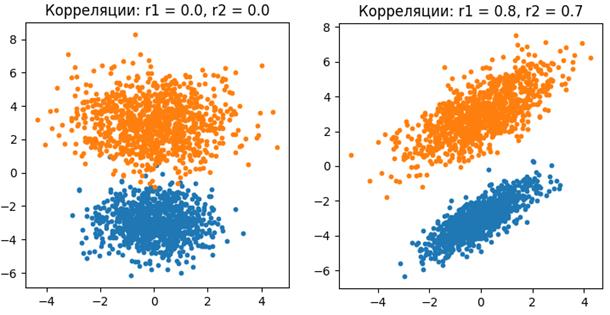
Существует теорема, которая доказывает, что эти оценки соответствуют оценкам максимального правдоподобия для n-мерных гауссовских распределений. То есть, эти оценки адекватны и, в общем случае, ничего лучшего здесь мы придумать не можем. Конечно, чтобы можно было доверять этим оценкам, число объектов каждого класса должно быть как можно больше. Иначе, просто не соберем достаточной статистики. Считается, что минимум – это 100 объектов одного конкретного класса. Но, желательно иметь от 1000 и более. Чтобы все это лучше понять, давайте применим этот подход (гауссовский байесовский классификатор) к смоделированной задаче бинарной классификации, в которой обучающая выборка сгенерирована на основе двумерного нормального распределения, со следующими параметрами:
Всего мы
генерируем по N = 1000 образов
выборки каждого класса. По этим данным вычисляем оценки МО и ковариационных
матриц:
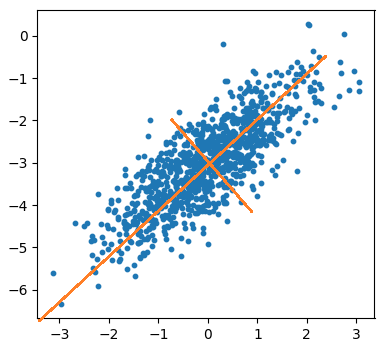
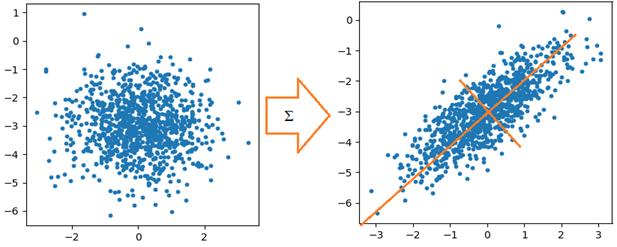
(Здесь от условной многомерной ПРВ был взят натуральный логарифм). Реализацию этого алгоритма на Python можно посмотреть в программе: Отличие гауссовского байесовского классификатора от наивной байесовской классификацииДавайте, теперь, внимательнее посмотрим, чем все-таки отличается гауссовский байесовский классификатор от его «наивной» реализации. Конечно, я уже отмечал, что ковариационной матрицей, но в чем суть этой матрицы? Что она, фактически, дает? Если еще раз посмотреть на распределение точек для двумерного гауссовского распределения с корреляцией 0,7, то можно увидеть, так называемый, их эллипс рассеяния. И в пределах этого эллипса можно выделить две главные оси, вдоль которых распределены точки:
Так вот, ковариационную матрицу можно представить в виде, так называемого, спектрального разложения:
где
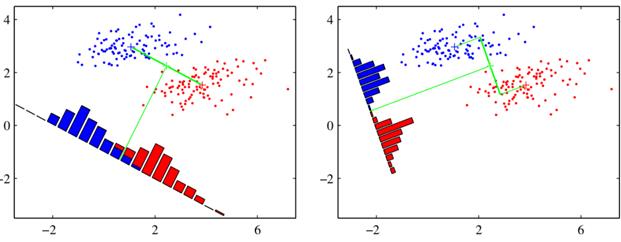
То есть, прописывая обратную матрицу в классификаторе, мы, по сути дела, переходим в новое пространство (новую систему координат), где признаки не коррелированы и там, в этом пространстве реализуем обычный, наивный байес (вычисляем сумму). Вот в чем основная суть ковариационной матрицы в гауссовском байесовском классификаторе.
Подробнее о спектральном разложении, собственных векторах и числах, мы с вами еще будем говорить на будущих занятиях. Но, я думаю, что общий принцип работы байесовских классификаторов при гауссовских распределениях вам понятен. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
- (по
прежнему) априорная вероятность появления класса 
; 
- условная
плотность распределения (функция правдоподобия) образов 
для заданного
класса 
- вектор
математических ожиданий образов 
- ковариационная
матрица образов 
- оператор
математического ожидания.
- штрафы,
которые мы накладываем на неверную классификацию моделью класса 
,
- n x n матрица,
состоящая из собственных векторов матрицы 
; S – диагональная
матрица с дисперсиями (собственными числами) по главной диагонали. Фактически,
ковариационная матрица определяет линейные преобразования равномерно
распределенного множества точек в коррелированное множество точек:
