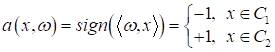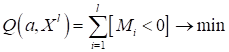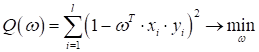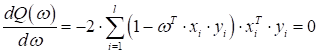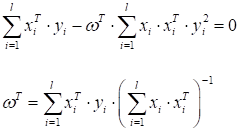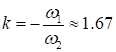Функции потерь в задачах линейной бинарной классификации

Практический курс по ML: https://stepik.org/course/209247/

На предыдущем занятии мы с вами рассмотрели простейший пример обучения модели бинарной линейной классификации вот в таком виде:

где  - вектор настраиваемых (в процессе обучения) параметров. И всю задачу свели к поиску всего одного коэффициента :

Кроме того, мы, фактически, придумали алгоритм для нахождения этого единственного коэффициента. Однако, хотелось бы свести эту задачу к задаче математической оптимизации по некоторому критерию качества, а также обобщить на произвольное число коэффициентов.

Начнем с определения показателя качества. На предыдущем занятии он у нас вычислялся по количеству неверно классифицируемых наблюдений (входных векторов):

Напомню, что здесь в качестве отступа мы используем величину:

а в качестве функции потерь:

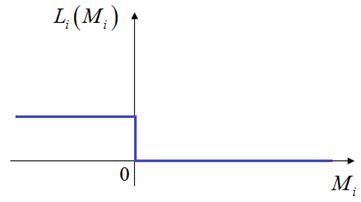
(Здесь квадратные скобки – это индикатор ошибки. В соответствии с нотацией Айверсона они возвращают 1 для True и 0 – для False).

Если изобразить эту функцию потерь, зависящую от отступа, то получим ступенчатый график:

Как вы понимаете, он не имеет производных в точках перегиба, да и во всех остальных производные будут равны 0. То есть, эта функция не подходит для задачи математической оптимизации при поиске весовых коэффициентов . Как же быть? Давайте немного схитрим и возьмем какую-нибудь похожую, но дифференцируемую функцию. И таких функций напридумывали огромное количество. Вот некоторые, наиболее известные:

• - кусочно-линейная (SVM);
•  - кусочно-линейная (Hebb’s rule);
•  - логарифмическая (LR);
•  - квадратичная (FLD);
•  - сигмоидная (ANN);
•  - экспоненциальная (AdaBoost).

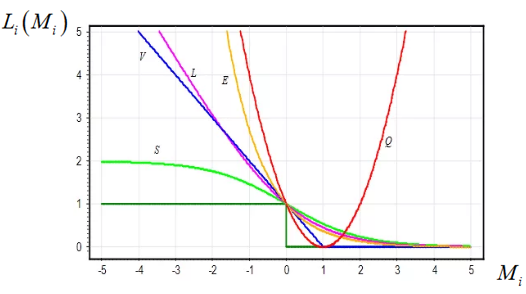
Особенность всех этих функций (помимо того, что они всюду дифференцируемы) в том, что они по значению больше, либо раны исходной пороговой. Следовательно, минимизируя любую из них, мы автоматически будем минимизировать потери и при пороговой функции.

Давайте посмотрим, как это можно использовать для квадратичной функции потерь:

Тогда функционал качества запишется в виде:

Здесь мы можем найти оптимальный вектор коэффициентов  чисто математически:

откуда

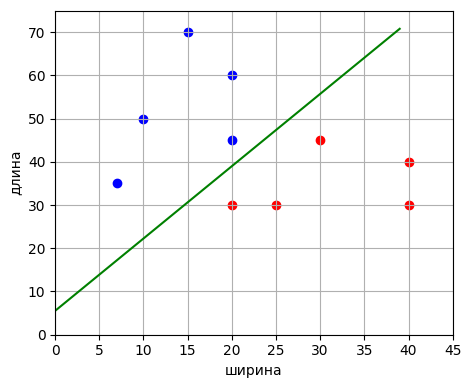
Давайте сделаем вычисления по этой формуле в программе на Python, применительно к нашей задаче бинарной классификации гусениц и божьих коровок:

Здесь каждое наблюдение представлено двумя признаками: ширина и длина. Но у нас, в общем виде вектор параметров  состоит из трех компонент:

(добавляется еще смещение), так как уравнение разделяющей прямой записывается в виде:

Поэтому мы добавим к нашим наблюдениям еще один признак – константу 1:

Программа на Python будет следующей:

machine_learning_7.py

После выполнения увидим значения коэффициентов:

[ 0.05793234 -0.0346272   0.1912188 ]

и график разделяющей линии:

То есть, здесь

и угловой коэффициент прямой:

Вот так просто мы решили ту же самую задачу бинарной классификации, но при этом использовали математический аппарат для поиска оптимальных коэффициентов. В этом одно из преимуществ замены пороговой не дифференцируемой функции на гладкие и всюду дифференцируемые. В различных известных методах классификации именно так и поступают – выбирают подходящие функции потерь и решают задачу минимизации эмпирического риска.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation