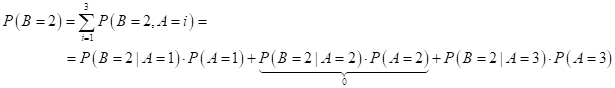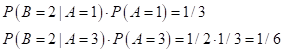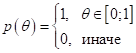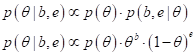Формула Байеса при решении конкретных задач

Практический курс по ML: https://stepik.org/course/209247/

На этом занятии я хочу вас поближе познакомить с формулой Байеса, которую в простейшем варианте для двух случайных событий A и B, можно записать в виде:

Впервые она была предложена английским богословом Томасом Байесом. В машинном обучении, на мой взгляд, эта формула имеет то же значение, что и знаменитая формула из физики:

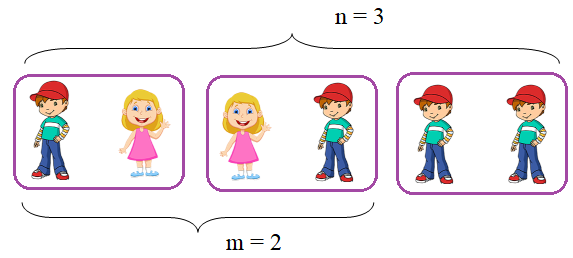
Почему так? В чем смысл формулы Байеса и что она нам на самом деле дает? Я начну с очень простой задачи.

Предположим, мы встречаем своего хорошего знакомого, с которым давно не виделись, и он нам сообщает, что у него двое детей и один из них мальчик. Спрашивается, какова вероятность, что другой ребенок девочка?

Чисто интуитивно, может показаться, что ответ 1/2, так как второй ребенок может быть либо девочкой, либо мальчиком. Но, что нам даст строгое математическое решение. В этой задаче мы можем просто перебрать все варианты и найти искомую вероятность, следующим образом.

Всего комбинаций из двух детей, где имеется хотя бы один мальчик, может быть три: n = 3. Но только в двух из них (m = 2) присутствует девочка. Следовательно, вероятность того, что другой ребенок девочка, равна:

Видите, каким неожиданным может быть ответ. Конечно, те из вас, кто хорошо знает теорию вероятностей, быстро догадались и, я надеюсь, пришли к верному ответу.

А теперь давайте, немного изменим формулировку задачи:

Мы встречаем своего хорошего знакомого и видим, что он ведет за руку мальчика. Какова вероятность, что другой ребенок девочка?

Ответ будет уже 1/2, так как второй ребенок может быть либо мальчиком, либо девочкой:

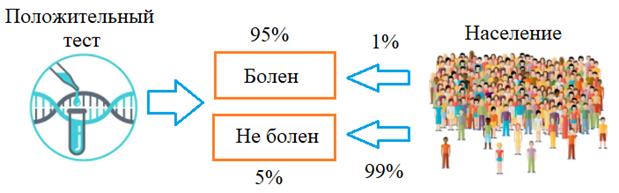
Опять же, обратите внимание, как от незначительного изменения формулировки совершенно меняется вычисление вероятности.

Теперь, когда я продемонстрировал вам коварство задач по теории вероятностей, рассмотрим пример, где формула Байеса, словно путеводная звезда, выведет нас из дебрей логических джунглей. Вот классическая задача такого типа.

Предположим, что некий тест на какую-нибудь страшную болезнь с вероятностью 0,95 (то есть, в 95 % случаях) не ошибается (дает верные результаты). Также известно, что этой болезнью страдает, в среднем, 1% населения (вероятность 0,01). Некий человек (совершенно случайный) получает положительный результат данного теста. Вопрос. С какой вероятностью он действительно болен?

Опять же, здесь легко представить ситуацию, что среднестатистический человек, мало знакомый с теорией вероятностей, прочитав эту инструкцию, увидев положительный результат своего теста, в панике хватается за голову, полагая, что жизнь его кончена. Но, давайте посмотрим, насколько он прав. Вначале, изобразим условия задачи:

И введем следующие события:

A: некий (случайный) человек из населения, болен;

B: тест показал положительный результат.

Нам нужно найти вероятность, что человек болен, при условии получения им положительного результата теста, то есть, условную вероятность:

В соответствии с формулой Байеса, эта вероятность определяется, как:

Нам осталось только разобраться, чему равны вероятности в правой части этой формулы. Очевидно, что

так как только 1% населения болеет этой болезнью. Следующая вероятность  - это вероятность положительного теста, при условии, что человек действительно болен. По условию задания, тест дает верные положительные результаты в 95% случаев, следовательно:

Наконец, последняя вероятность  - это вероятность того, что тест покажет положительный результат (вне зависимости от того, болен человек или нет). Эту величину можно вычислить, следующим образом:

То есть, мы тестируем все население, и смотрим, какова доля положительных результатов теста.

Все, осталось подставить все эти величины в формулу Байеса и получить вероятность того, что человек действительно болен при положительном результате теста:

Не так уж и много, как могло показаться на первый взгляд! У этого человека есть все шансы оказаться на самом деле здоровым.

Вот это показательный пример того, как формула Байеса нам помогает верно найти вероятность события, исходя из заданных условий в задаче. И вывод нередко оказывается неожиданным.

Давайте, я покажу еще одну интересную задачу того же рода, взятую из реальной жизни. С 1963 по 1976 годы в Америке проводилась телевикторина под названием «На что спорим?». Ее ведущим был Монти Холл. И однажды, там прозвучала задачка, которая в свое время удивила многих обывателей и даже специалистов в этой области. Звучала она примерно так.

Представьте, что перед вами три закрытые двери: за двумя из них по козе, а за одной – автомобиль Мазератти. Разумеется, вы не знаете где что находится. Ведущий предлагает вам выбрать одну из трех дверей. После этого он открывает другую дверь, за которой находится коза и спрашивает: хотите ли вы поменять свое решение? То есть, по сути, он спрашивает: повысится ли шанс выиграть автомобиль, если изменить свое решение и выбрать другую закрытую дверь?

Опять же, обыденная интуиция говорит нам о бессмысленности изменения решения, так как вероятность выиграть автомобиль, после открытия одной двери, становится 1/2 (либо за выбранной дверью, либо за другой, не выбранной). Давайте проверим нашу интуицию с помощью формулы Байеса?

Введем две случайные величины:

A – машина за 1-й, 2-й или 3-й дверью;

B – ведущий открыл 1-ю, 2-ю или 3-ю дверь.

Соответственно, вероятности:

так как машина может быть спрятана (равновероятно) за одной из трех дверей. Далее, нам нужно предположить (без потери общности), что мы выбираем какую-либо дверь, например, 3-ю, как показано на рисунке, а ведущий открывает 2-ю дверь. Это будет влиять на вычисление последующих вероятностей. То есть, мы хотим вычислить вероятность выиграть автомобиль, при смене двери:

Распишем формально эту формулу:

Вероятность  нам известна. Следующая вероятность  показывает, что ведущий открывает 2-ю дверь, если мы изначально выбрали 3-ю дверь, но автомобиль находится за 1-й дверью. Как думаете, какие варианты здесь есть у Монти Холла? Да, никаких, ему придется открыть именно 2-ю дверь, т.к. остальные либо заняты, либо там автомобиль (с автомобилем он не открывает). Получаем вероятность такого исхода:

Наконец, последняя вероятность:

Здесь два ненулевых слагаемых:

Получаем вероятность выигрыша автомобиля при смене двери:

Впервые верно эту задачу решила Мэрилин вос Савант аж в 1990 году. До этого многие годы наивно полагали, что вероятность выигрыша не меняется при смене двери и составляет 1/2 после того, как ведущий открыл одну из них. Поначалу ее решение повергло в шок и возмутило своим невежеством не только простых обывателей, но даже маститых профессоров математики! Среди несогласных был известнейший математик Палу Эрдёшу. Он стоял на своем, даже после математического доказательства правильности ответа Мэрилин. И сдался только тогда, когда было проведено компьютерное моделирование данной задачи и показана справедливость ее рассуждений. Да, что говорить, даже у меня под видео по теории вероятностей, где я описал эту задачу, следы ожесточенных дискуссий о верности выводов. Поэтому решил, пользуясь случаем, доказать, что все верно.

Во всех этих примерах с помощью формулы Байеса мы пересчитываем известные нам вероятности событий в вероятность другого события, которое было бы сложно определить как то еще, например, исходя из здравого смысла. В машинном обучении все ровно также. Только используется теорема Байеса, применительно к плотностям распределения случайных величин:

Как правило, мы относительно просто можем найти распределение целевых значений , условное распределение образов  для каждого целевого значения, а априорное распределение образов  часто можно отбросить в задачах оптимизации. Затем, опираясь на эту входную информацию, делать прогноз целевого значения . Подробнее об этом мы поговорим уже на следующем занятии.

Формула Байеса для плотностей распределения

Все это были относительно простые задачи, где формула Байеса помогает нам не ошибиться с выводами. Давайте теперь приблизимся к задачам машинного обучения и рассмотрим следующий сюжет. Предположим, некоторая майнинговая ферма генерирует биткоины и эфириумы:

Каждый день она формирует либо биткоин, либо эфириум. И мы бы хотели оценить вероятность появления биткоина θ. Причем, обратная вероятность появления эфириума, будет:

так как в течение дня выходит либо первая монетка, либо вторая, но не обе вместе.

Предположим, что мы тайные агенты, нанятые конкурирующей фермой, и все, что можем сделать – это наблюдать, какая монетка появится. Допустим, за месяц наблюдений, было зафиксировано b биткоинов и e эфириумов. Чтобы не сидеть в засаде еще месяц и не морозить уши, тайные агенты решили по этой информации вычислить вероятность параметра θ. Так как они хорошо учились в школе, а потом и в вузе, то первым делом записали теорему Байеса для решения этой задачи:

Им не составило труда понять, что множитель  - это априорное распределение неизвестного параметра θ, то есть, наши знания о том, как может меняться этот параметр. Очевидно, он должен быть в пределах от 0 до 1 (это же вероятность). Поэтому они выбрали равномерное распределение:

Следующее распределение  должно показывать значения вероятностей появления b биткоинов и e эфириумов при вероятности появления биткоина θ:

А вот с совместной вероятностью  возникли проблемы и они решили ее просто выбросить из этой формулы, так как эта ПРВ не зависит от нужного им параметра θ. В итоге всех этих скрупулезных математических выкладок, получилось:

Что делать дальше? Вспомнив курс «Машинное обучение», наши шпионы применили метод максимума правдоподобия для нахождения точечной оценки параметра θ:

Причем, здесь уже можно записать равенство, так как точка максимума у обоих выражений будет одной и той же. Далее:

К этому ключевому моменты удалось прийти, благодаря использованию формулы Байеса и методу максимального правдоподобия. Остался последний шаг. Продифференцировать выражение по θ и приравнять результат нулю. Но, чтобы было проще считать, было взято эквивалентное выражение:

В итоге:

откуда

Как видите, при простых предположениях об априорном распределении и знании функции потерь , получили очевидный результат – долю биткоинов среди общего количества монет. Благодаря формуле Байеса наши шпионы успешно выполнили задание и разошлись по домам.

Все это были примеры использования теоремы Байеса для решения разных, жизненных задач. На следующем занятии мы увидим, как эта формула используется в задачах машинного обучения.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation