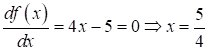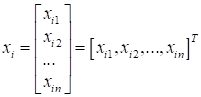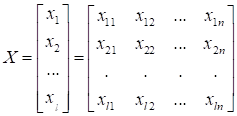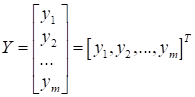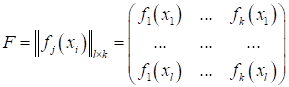|
Что такое машинное обучение? Обучающая выборка и признаковое пространствоПрактический курс по ML: https://stepik.org/course/209247/ Здравствуйте, дорогие друзья! Мы начинаем курс «Основы машинного обучения». Сразу отмечу, что это курс с математическим уклоном. Поэтому для его восприятия необходимо хорошо знать математическую базу:
Кроме того, на занятиях я буду использовать язык Python при реализации отдельных задач. Это необходимый минимум для начала изучения данного предмета. Далее, я буду полагать, что вы владеете этим материалом. Конечно, машинное обучение – это целый мир и при разработке этого курса я активно пользовался сторонними источниками. Лучший охват этой темы в русскоязычном сегменте, на мой взгляд, дает профессор К. В. Воронцов. Ссылку на него вы найдете под этим видео. Для меня это было самое квалифицированное, понятное и полное изложение материала по данной теме с достаточно глубоким математическим уклоном и в то же время очень доступное. Я взял его курс лекций за основу своего курса. Кое что упростил, дополнил, в общем, это ни в коем случае не плагиат. Помимо этого мне очень помогла книга С. Николенко «Глубокое погружение». Он рассматривает задачи машинного обучения с позиции теории вероятностей, что бывает очень полезно для понимания некоторых деталей. Также рекомендую его курс на ютуб (ссылка также под этим видео). Но он, скорее для тех, кто хорошо владеет математическим аппаратом теории вероятностей и математической статистики. Для новичков в этой области будет сложновато. Конечно, я пользовался по мелочам и другими источниками. Сейчас все их уже и не вспомню. Плюс собственный скромный опыт по этой тематике. Но основные первоисточники я вам указал и советую их также посмотреть, так как там вы найдете очень много дополнительного материала. В целом, я постарался сделать именно введение в машинное обучение для тех, кто мало касался прежде этой темы и хотел бы разобраться в основах этого направления. А уже потом, думаю, будет гораздо понятнее и проще проходить курс профессора К. В. Воронцова и погружаться в другие полезные материалы. Но, вернемся теперь непосредственно к нашей теме и давайте вначале разберемся, что скрывается за фразой машинное обучение. По простому – это алгоритмы, которые можно обучать, то есть, настраивать под решение конкретных задач. И здесь сразу возникают вопросы: что это за задачи и как выполняется настройка алгоритмов? Начнем с первого. Далеко не все задачи следует решать методами машинного обучения. Например, если нам нужно найти точку минимума какой-либо функции, для простоты возьмем параболу:
то ее легко решить классическими методами. Здесь достаточно вычислить производную по аргументу и приравнять ее к нулю:
Все, никаких алгоритмов машинного обучения не требуется. И везде, где можно относительно просто (с математической и вычислительной точки зрения) получить требуемый результат, не нужно применять никаких сложных, обучаемых алгоритмов. А где без машинного обучения не обойтись или классическое решение задачи становится довольно сложным? Самый простой и очевидный пример – это классификация изображений. Например, нужно уметь различать кошек от собак, или идентифицировать человека по отпечатку пальца, или найти аномалии на рентгеновских медицинских снимках и т. п. Здесь везде исходные данные (изображения) имеют сложную структуру и непонятно, как чисто математически описать универсальный алгоритм, который бы выдавал корректные результаты (в данном случае классификации). Поэтому идут на некоторую хитрость – создают алгоритм такой, чтобы он сам в процессе обучения сформировал нужные критерии для решения задачи. В частности, это хорошо делают глубокие нейронные сети особенно в области распознавания образов на изображениях. Но об этом позже. Главное здесь понять, что не нужно «совать» алгоритмы машинного обучения в первую попавшуюся задачу, возможно, она имеет гораздо более простое (в вычислительном плане) решение. И общее правило здесь такое: если ничего не помогает, то посмотрите в сторону обучаемых алгоритмов, которые могут дать приемлемое, но далеко не всегда точное решение. Так какие же вообще существуют задачи машинного обучения? Обычно выделяют следующие категории:
Задача классификации – это когда требуется входные данные отнести к тому или иному классу (например, изображения разделить на кошек и собак, или распознать произнесенное слово, или по медицинским данным выдать диагноз и т.п.). В задачах регрессии обычно делают прогнозы в виде вещественных чисел на основе входных данных (например, оценка курса валют по предыдущим показаниям, или прогноз объема продаж товара определенного вида, или просто построить прогноз некоторой функции по измеренным эмпирическим данным и т.д.). Наконец, третий тип задач подразумевает упорядочивание (по некоторому критерию) входного набора данных. Классический пример – это поисковые системы, которые ранжируют поисковую выборку по релевантности для каждого конкретного пользователя. Все эти задачи, как правило, решаются с применением алгоритмов машинного обучения, т.к. входные данные имеют достаточно сложную структуру, а значит, нужно построить нетривиальные критерии для их обработки. Сделать это человеку часто просто не под силу, поэтому нужно подключать процесс обучения по так называемой обучающей выборке. Обучающая выборкаИ вот здесь мы подошли к первому важному моменту – что из себя представляет обучающая выборка? Изначально – это некие исходные данные, прямые результаты измерений. Это может быть то же самое изображение, звуковой сигнал, измерения роста, веса человека и т.п. Обычно все эти данные представляются набором некоторых чисел (все же мы имеем дело с вычислительной техникой, а она воспринимает только числа). Все эти измерения удобно представлять единым образом в виде векторов. Я буду их обозначать, следующим образом:
(черточку сверху указывать не стану, т.к. по ходу изложения это будет и так понятно). Здесь представлено измерение некоего i-го объекта. Например, так можно представить i-е изображение, если все его пиксели вытянуть в одну строку – в один вектор, или амплитуды звукового сигнала, или пары измерений веса и роста. Я, думаю, понятно, что вектором можно представить любой набор измерений. Далее, мы все эти наборы можем составить в матрицу:
В данном случае
матрица X составлена из Но матрица X это еще не обучающая выборка. Нам здесь для полноты картины не хватает выходных данных:
Их еще называют целевыми (target). Что это за выходы? Например, в задачах классификации они могут принимать одно из следующих значений:
В задачах регрессии каждый вход связан с одним или несколькими вещественными числами:
В задачах ранжирования:
И вот вся эта
совокупность данных Но и это еще не
все. Исходные результаты измерений На уровне математики извлечение признаков из сырых исходных данных можно представить в виде функционального (в широком смысле этого слова) преобразования:
Здесь x – это вектор
результатов исходных измерений, который затем, переводится в набор признаков,
причем В результате, можно записать матрицу F, содержащую эти выделенные признаки:
Получаем новое признаковое пространство F, упрощающее работу алгоритмов машинного обучения. На этом мы завершим наше первое занятие. На следующем продолжим эту тему и формализуем математически подход к задачам обучения алгоритмов. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
векторов
и каждый вектор содержит n чисел. Кстати, в общем случае,
размерность этих векторов может меняться, но обычно, в задачах машинного
обучения их стараются делать равными. Так с ними проще работать.
- при бинарной
классификации;
-
при M-классовой
классификации (классы не пересекаются);
-
при M-классовой
классификации с пересекающимися классами (здесь M – это
размерность пространства).
-
одномерная
задача регрессии;
- m-мерная
задача регрессии.
уже
может выступать в качестве обучающей выборки, так как каждому входному вектору
(наблюдению) 
поставлено
в соответствие значение (или вектор) 
.
Такие данные еще называют размеченными и являются, своего рода,
«золотом», «валютой» для алгоритмов машинного обучения, т.к. их формирование,
зачастую, - это самый сложный и длительный процесс, требующий участие одного
или группы людей.
могут
иметь сложную структуру (например, при кодировании текстов, звуков или
изображений) и трудно интерпретируемыми самими алгоритмами. В частности, до
появления глубоких нейронных сетей (deep learning) в задачах
классификации изображений инженеры формировали, так называемые, вторичные
признаки: выделяли различные монотонные области, границы объектов с помощью
различных фильтров. Доходило даже до того, что набрасывали на изображение
случайные линии и пытались, затем, вычислять различные соотношения площадей. И такие
подходы в разных задачах давали определенные результаты. По-английски это
называется feature extraction и feature engineering – непростой и
творческий процесс, создания более информативных признаков.
-
любое число, не обязательно равное n (исходному числу признаков –
длина вектора 
).
