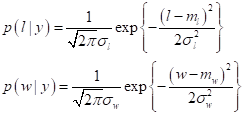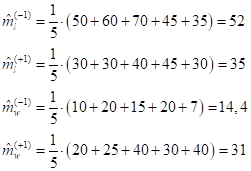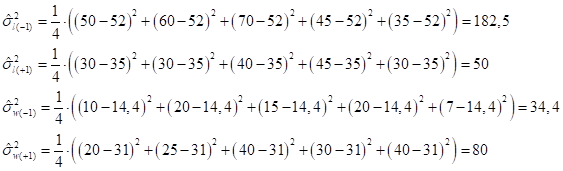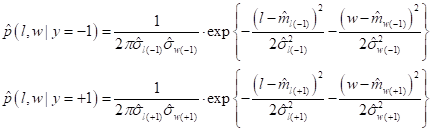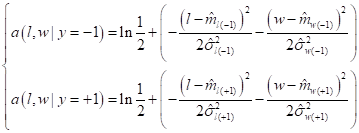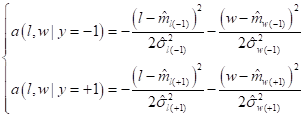Байесовский вывод. Наивная байесовская классификация

Практический курс по ML: https://stepik.org/course/209247/

Давайте предположим, что мы рассматриваем некоторую задачу классификации. Для простоты, бинарную (двухклассовую): . И, конечно же, имеется набор данных обучающей выборки:

Эти данные подчиняются некоторой совместной плотности распределения вероятностей (ПРВ) . Условно она изображена на рисунке ниже (здесь  - весь трехмерный график целиком):

Наша задача отнести каждый конкретный входной вектор (образ)  к одному из двух классов . Как это правильно сделать? Да, отнести вектор  к тому классу, вероятность которого окажется наибольшей. То есть, нам нужно найти вероятности для классов , а затем, выбрать наибольшее значение:

Используя теорему Байеса, это выражение можно расписать, следующим образом:

Я здесь через заглавную букву P обозначил вероятность события, а через малую букву p – ПРВ.

В этой формуле множитель  - это априорная вероятность появления класса  (доля соответствующего класса в обучающей выборке);  - распределение образов  для определенного класса . На рисунке, образно, распределение первого класса показано голубым графиком, а второго класса – красным графиком. Наконец,  - распределение образов всех классов безотносительно к их принадлежности тому или иному классу.

Предположим, мы знаем величины  и распределения . Тогда, правило выбора класса (модель классификации) можно записать, следующим образом:

Обратите внимание, я здесь отбросил распределение , так как оно не зависит от параметра , а значит, не влияет на положение точки максимума.

Вот так, с позиции теоремы Байеса, ставится задача классификации в машинном обучении. Причем, число классов может быть не два, а сколько угодно, ограничений здесь никаких нет.

Оптимальный байесовский классификатор

Вообще, на практике в эту модель добавляют еще множители , которые определяют величину штрафа при неверной классификации для каждого класса :

Существует теорема, которая доказывает, что в этом случае будут минимизироваться средние ошибки, то есть, функционал вида:

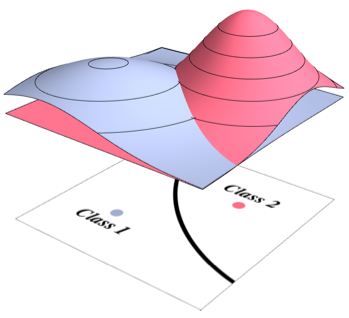
Минимизация данного критерия соответствует оптимальному байесовскому классификатору. Подробно о нем я уже рассказывал:

https://www.youtube.com/watch?v=OhIp6qJkvCI

По этой ссылке вы также найдете пример простой байесовской классификации мужчин и женщин по двум признакам: высота и вес.

Получается, что если бы мы знали совместную ПРВ , то задача классификации в машинном обучении была бы полностью решена. Вся проблема заключается в том, что эта ПРВ неизвестна и нам ее приходится как то оценивать. Или же, решить более простую задачу, найти оценки:

по обучающей выборке.

Конечно, после того, как в байесовский классификатор подставляются оценки ПРВ, то он перестает быть оптимальным. Поэтому оптимальность здесь, скорее, представляет теоретический интерес. На практике, реальные классификаторы могут лишь приближаться к оптимальному.

Наивный байесовский классификатор

Главная проблема в реализации байесовского классификатора – это оценить условные ПРВ . И, в общем виде, эта задача гораздо сложнее, чем построение классификатора с позиции выбора параметрической функции и последующего поиска вектора параметров :

То есть, так, как это мы делали с самого начала. Значит, байесовский (вероятностный) подход к задачам машинного обучения – это лишь интересный теоретический трюк? Не совсем. Во-первых, как мы уже видели, он дает лучшее понимание работы алгоритмов машинного обучения. А, во-вторых, мы можем упростить задачу оценки многомерной условной ПРВ , положив, что все признаки:

независимы между собой. В этом случае многомерная ПРВ расписывается через произведение соответствующих одномерных ПРВ:

Такое, вообще говоря, сильное предположение о независимости признаков, приводит нас к алгоритму, известному под названием наивный байесовский классификатор:

Или, эквивалентный вывод часто делают по логарифму от произведения величин (уходят от произведений):

Как видите, мы здесь оперируем только одномерными ПРВ и это сильно упрощает задачу, т.к. восстановить одномерную плотность гораздо проще, чем многомерную.

И еще одно важно замечание. Часто в сторонних библиотеках алгоритм наивного байесовского классификатора реализуют с использованием гауссовских ПРВ . Конечно, это достаточно распространенный случай, но не всегда признаки подчиняются нормальному закону распределения. Если в вашей задаче существенно иная ПРВ признаков, то библиотечные реализации могут приводить к неудовлетворительным результатам. Обращайте на это внимание. Иначе, вы рискуете сделать вывод о неприменимости наивного байеса для решения вашей задачи, тогда как на самом деле нужно просто выбрать другой вид ПРВ.

Пример задачи классификации наивным байесовским классификатором

В заключение этого занятия приведу пример использования наивного байесовского классификатора для уже знакомой нам задачи разделения гусениц и божьих коровок.

Обучающая выборка задана таблицей с двумя классами :

Будем предполагать, что признаки ширина и длина независимы и подчиняются нормальному закону распределения:

где l (length) – длина жука; w (width) – ширина;  - математические ожидания для длины и ширины соответственно;  - дисперсии для ширины и длины соответственно.

Наша задача определить параметры гауссовских распределений по обучающей выборке. Сначала найдем МО (средние значения) признаков для обоих классов (как средние арифметические):

А, затем, дисперсии по формуле:

получим:

Далее, сформируем условные ПРВ для первого и второго классов по правилу:

И в итоге получаем следующее:

Осталось определить априорные вероятности появления классов в выборке. В нашем случае они будут равны:

так как имеем по 5 объектов каждого класса.

Все вероятности и ПРВ определены. Теперь можно построить классификатор по правилу:

Величины штрафов возьмем одинаковыми для обоих классов:

получим:

И, так как слагаемое  одинаковое у обоих классов, то его можно не учитывать:

Все, мы с вами получили алгоритм классификации. Здесь нужно вычислить величины  и отнести объект  к классу с наибольшим значением.

Реализацию этого алгоритма на Python можно посмотреть по ссылке:

machine_learning_16.py

Я, думаю, что вы теперь представляете общий принцип построения байесовского классификатора и реализацию его в простейшем случае по методу наивного байеса.

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation