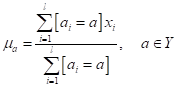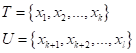|
Алгоритм кластеризации Ллойда (K-средних, K-means)Практический курс по ML: https://stepik.org/course/209247/ На этом занятии рассмотрим один из самых простых алгоритмов кластеризации – алгоритм Ллойда (его еще называют методом K-средних). Идея его очень проста. Изначально, у нас имеется набор объектов
каждый из которых представлен в n-мерном числовом признаковом пространстве:
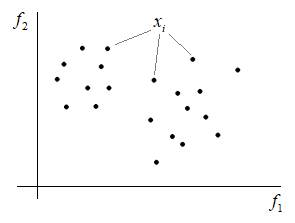
Например, если каждый объект имеет два признака (n = 2), то множество объектов можно представить в виде точек на плоскости:
Наша задача разбить это множество объектов по группам (кластерам). Для этого в алгоритме Ллойда задается:
Да, мы здесь изначально должны явно указать алгоритму, на сколько групп следует разбивать объекты выборки. Сам он не определяет число кластеров. Определяется метрика – способ вычисления расстояний между произвольными двумя точками в признаковом пространстве:
Например, часто используют евклидовое расстояние:
Далее, для каждого кластера нам нужно задать начальные центры. Это можно сделать или случайным образом, или взять любые K объектов и считать их центрами:
После этого запускается итерационный процесс, в котором выполняются следующие действия:
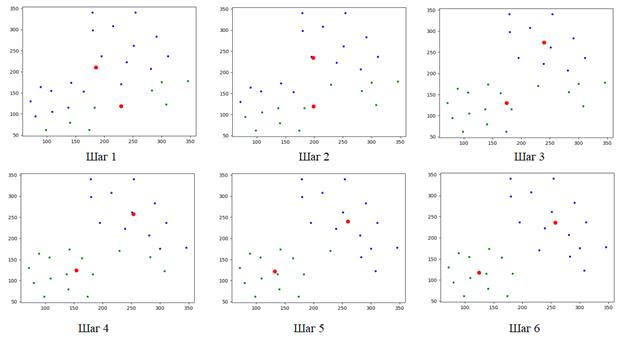
И так до тех пор, пока положения центров не будут меняться (или меняются очень незначительно). Вот пример того, как выполняется кластеризация объектов в двумерном метрическом признаковом пространстве при двух кластерах (K = 2): machine_learning_33_animate.py
Здесь красные точки – это центры кластеров, синие точки – первый кластер, зеленые – второй кластер. Алгоритм сошелся (то есть, центры кластеров перестали изменяться) за шесть шагов. Существует теорема, которая доказывает, что алгоритм Ллойда сходится всегда к некоторому равновесному состоянию при любом наборе данных и любой размерности признакового пространства с выбранной метрикой. Фактически, здесь итерационно решается оптимизационная задача минимизации суммарных внутрикластерных расстояний:
Вы можете заметить, а как же второй параметр максимизации межкластерных расстояний, который мы вводили на предыдущем занятии:
В алгоритме Ллойда его просто не учитывают. Сам алгоритм для объектов в двумерном признаковом пространстве реализован на языке Python и его можно посмотреть по ссылке: Алгоритм Ллойда при частично размеченной выборкеБывают задачи, в
которых часть (k объектов) из обучающей выборки
размечены, а остальные
Это вариант (пример) задачи частичного обучения без учителя (SSL). В этом случае алгоритм Ллойда, в целом, сохраняется, только разбиение на кластеры выполняется для объектов множества U. Вначале мы также
задаем число кластеров
Затем, в цикле выполняем два действия:
Как видите, алгоритм практически тот же самый. В качестве небольшого домашнего задания, попробуйте его самостоятельно реализовать. Недостатки алгоритма ЛлойдаКонечно, основным преимуществом алгоритма Ллойда является его простота (скорость работы). И для относительно несложных задач он вполне пригоден. Но есть и очевидные недостатки:
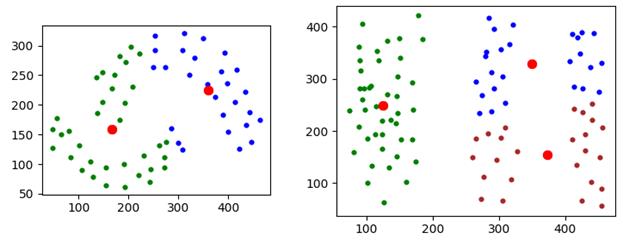
Вот примеры неудачного разбиения объектов на кластеры. Причина, в общем то, одна – существенная негауссовость распределений точек в каждой группе. То есть, алгоритм K-средних (K-means) пытается покрыть выборку «шариками» и отсюда такой результат. На следующем занятии мы рассмотрим более совершенный алгоритм кластеризации DBSCAN, который лишен некоторых недостатков алгоритма Ллойда и дает, в целом, лучшие результаты. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
-
число кластеров.
- номера
кластеров
относится
к ближайшему центру 
в
соответствии с выбранной метрикой 
:
-
не размечены:
и
формируем центры кластеров:
относим
к ближайшему кластеру (ближайшее расстояние до центра):
