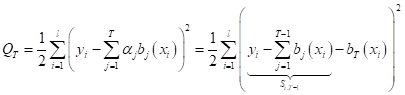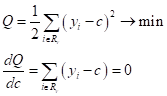|
Алгоритм AdaBoost в задачах регрессииПрактический курс по ML: https://stepik.org/course/209247/ На предыдущем
занятии мы с вами увидели, как работает алгоритм AdaBoost (Adaptive Boosting) применительно
к задачам бинарной классификации с метками классов Я напомню, что при бустинге мы обучаем T алгоритмов, а затем, вычисляем взвешенную сумму:
Причем, поиск весов и алгоритмов выполняется по «жадному» принципу: мы фиксируем все ранее найденные элементы:
для нахождения
текущих Так как мы решаем задачу регрессии, критерий качества обычно формируют при использовании квадратичной функции потерь:
То есть, мы
проходим по всем объектам обучающей выборки Если расписать
величину
Здесь можно
заметить, что, во-первых, в задачах линейной регрессии множители
И, во-вторых, при фиксированных предыдущих весах и алгоритмах, мы, фактически, на шаге T минимизируем остаточные значения:
Далее, нам нужно
определиться с выбором семейства алгоритмов Итак, если
выбрать решающие деревья, то в задачах регрессии, при квадратичной функции
потерь, в листах сохраняются средние значения целевых меток
откуда
Обратите внимание, что при другой функции потерь, величина c может вычисляться по другому. В итоге, псевдокод алгоритма AdaBoost применительно к задачам регрессии, будет иметь вид: Вход: обучающая выборка
Выход: набор базовых
алгоритмов 1: начальная
инициализация остатков:
2: для
всех
3: найти наилучший текущий алгоритм по правилу:
4: обновить остатки:
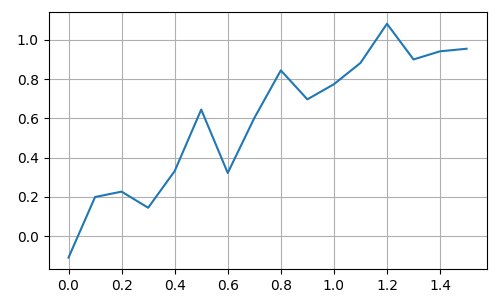
Реализация алгоритма AdaBoost для задач регрессии на PythonКак видите, все достаточно просто. Давайте теперь реализуем этот алгоритм на Python. Предположим, что нам нужно аппроксимировать (восстановить) значение функции:
где
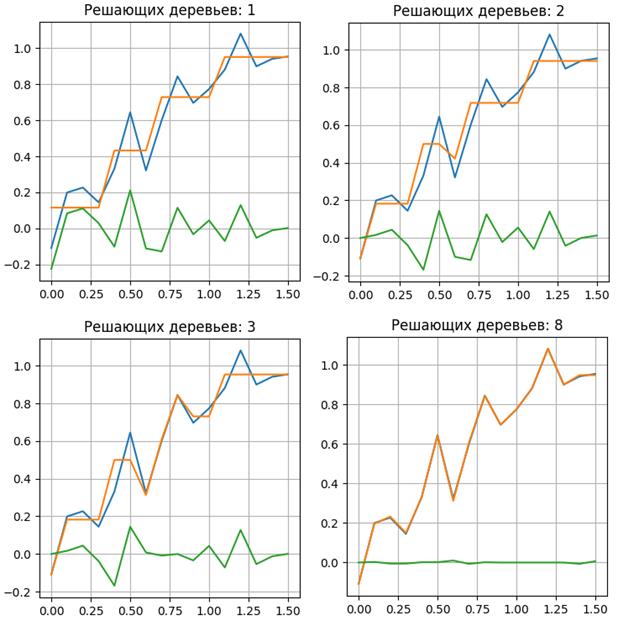
В качестве базовых алгоритмов будут выступать решающие деревья заданной максимальной глубины. Сам алгоритм можно скачать по ссылке: machine_learning_43_adaboost_regression.py Получаем следующие результаты восстановления исходного сигнала:
Как видите, с
увеличением числа базовых алгоритмов растет точность описания исходных целевых
значений Основные рекомендацииМы с вами рассмотрели классический алгоритм бустинга AdaBoost для задач классификации и регрессии. При этом, в задачах классификации используется экспоненциальная функция потерь:
а в задачах регрессии – квадратичная:
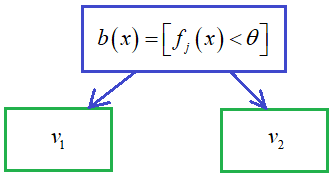
В итоге, эти функции приводят к несколько разным алгоритмам бустинга. Далее, в бустинге чаще всего используются решающие деревья в качестве базовых алгоритмов, или даже решающие пни, то есть, дерево с одной корневой вершиной и двумя листами:
При этом рекомендуется выбирать семейство простых алгоритмов, не обладающих хорошими обобщающими свойствами. Например, если взять тот же SVM и попробовать над ним реализовать бустинг, то особого эффекта не будет. Алгоритмы, которые сами по себе хорошо решают задачи классификации, регрессии или ранжирования объединять в композицию не имеет смысла. Как показала практика, улучшений особых достичь не получается. А вот деревья при объединении дают новое качество результирующего алгоритма и в ряде случаев обходят тот же SVM, нейронные сети и другие эффективные методы. Следующий момент, на который следует обратить внимание, - это наличие шумовых выбросов в обучающей выборке. При таких данных классический бустинг начинает работать значительно хуже. Однако, с этим можно бороться, если в алгоритме классификации AdaBoost отсеивать объекты с большими значениями весов. Я напомню, что вес объекта постепенно увеличивается, если он плохо обрабатывается композицией. И, скорее всего, является шумовым. Поэтому, при дальнейшем обучении последующих алгоритмов, такие объекты рекомендуется просто отбрасывать. Недостатки алгоритма AdaBoost
Я думаю, что теперь вы в целом представляете, как работает классический алгоритм AdaBoost. На следующем занятии мы продолжим эту тему и увидим, как можно обобщить этот подход на произвольные функции потерь, используя градиентные алгоритмы. Практический курс по ML: https://stepik.org/course/209247/ Видео по теме |
. Но
остается вопрос, как можно использовать этот подход в задачах регрессии? Как
раз об этом сейчас и пойдет речь.
и 
и 
.
и
вычисляем сумму квадратов ошибок.
, то
получим:
можно
отбросить, т.к. они лишь определяют масштабы выходных ответов алгоритмов. Этот
масштаб может формировать и сам алгоритм:
задачи
регрессии. Частым случаем являются решающие деревья, как и в задачах
классификации. Вообще, бустинг над решающими деревьями – это классика – наиболее
частый вариант его применения. Хотя, можно брать и любые другие семейства,
например, набор линейных алгоритмов или какие-либо еще. Главное, чтобы мы могли
относительно быстро (с вычислительной точки зрения) формировать, а затем
использовать эти алгоритмы.
объектов,
которые в них попадают. Это, как раз то, что нам нужно. Если представить, что в
некоторую листовую вершину попали M объектов 
обучающей
выборки, то оптимальное значение для их описания, можно найти из уравнения:
и
параметр T (число
алгоритмов в композиции)
- гауссовские
СВ с нулевым средним и дисперсией 0,1.
