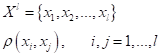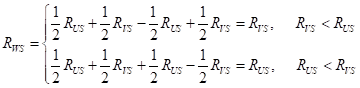Агломеративная иерархическая кластеризация. Дендрограмма

Практический курс по ML: https://stepik.org/course/209247/

Продолжаем рассматривать типовые алгоритмы кластеризации и на очереди алгоритм иерархической кластеризации. В чем суть такого подхода? Предположим, у нас имеется набор данных в числовом признаковом пространстве с заданной метрикой:

Для удобства я изображу их как точки в двумерном пространстве (хотя, в общем случае, пространство имеет n размерностей – по числу признаков). Далее, мы иерархически их либо объединяем, либо разбиваем на более мелкие кластеры. При объединении, изначально, каждый кластер содержит по одному объекту, а затем, на каждой итерации происходит объединение двух ближайших кластеров, образуя все более крупные группы. На практике, в основном используют идею последовательных объединений (агломерации) объектов. Отсюда и пошло название агломеративная иерархическая кластеризация.

Одним из первых ученых, который предпринял такой подход к данным, был Карл Линней, который пытался по своей объемной картотеки растений и животных объединить их по родами и видам:

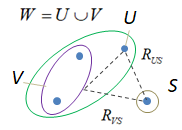
Полученные группы объектов, близких по определенным признакам, также называют таксонами. Фактически, таксон и кластер – это одно и то же и я буду использовать эти слова как синонимы.

Давайте подробнее рассмотрим идею агломеративной кластеризации, как наиболее часто используемую на практике. Итак, изначально мы имеем набор данных и каждый объект – это независимый кластер. Затем, в соответствии с заданной метрикой между объектами:

выбираем два ближайших таксона U, V и объединяем их в один W:

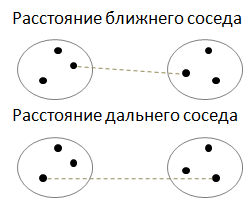
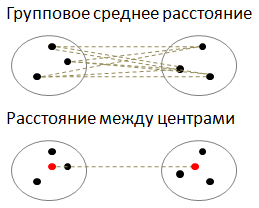
Этот шаг мы легко выполнили, так как умеем вычислять расстояния между отдельными объектами данных. Но теперь, у нас появилась группа из двух объектов. И нам нужно уметь вычислять расстояния от нее до всех остальных объектов выборки. Как это сделать? Тут имеется множество эвристик:

Так вот, оказывается, все эти варианты можно описать одной математической формулой:

где  - некоторые параметры, определяющие вид метрики между кластерами. Это выражение называется формулой Ланса-Уильямса и для указанных способов вычислений расстояний между таксонами, коэффициенты принимают вид:

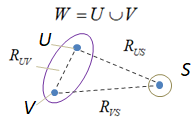
Чаще всего на практике используют расстояние дальнего соседа и расстояние Уорда, т.к. они приводят, как правило, к лучшим результатам кластеризации.

Давайте теперь детальнее разберемся, как работает формула Ланса-Уильямса. Проще всего показать ее принцип на одном объединенном таксоне W с двумя объектами и второго таксона S – с одним объектом:

Здесь отмечены все составляющие формулы. Предположим, что мы выбрали расстояние ближнего соседа, для которого:

и вычисление расстояния между кластерами W и S происходит, следующим образом:

Смотрите, если здесь раскрыть модуль, то получим:

А это есть не что иное, как выбор минимального расстояния между точками таксонов. В итоге, мы нашли расстояние между таксоном W и таксоном S. Потом, когда нам придется таксон из двух объектов объединять с другим таксоном, то при вычислении расстояния объединенного кластера W мы будем использовать ранее вычисленное расстояние  для получения нового  уже для кластера из трех объектов:

То есть, U, V и S здесь могут быть не только отдельными точками, но, по мере объединения (работы алгоритма), и кластерами с произвольными числом точек. Благодаря рекуррентному вычислению расстояний между объединяемыми таксонами и всеми остальными, мы, на каждой итерации алгоритма, имеем полную информацию о расстояниях между любыми парами сформированных кластеров.

Вот это ключевой момент работы алгоритма агломеративной иерархической кластеризации. По аналогии работают и все остальные метрики с другими значениями коэффициентов .

В результате, получаем следующий алгоритм иерархической кластеризации:

1:  - множество одноэлементных кластеров

 - метрика (расстояние) между отдельными объектами

2: для всех  ( - номер итерации)

3:       найти в  пару кластеров U, V с минимальным расстоянием

4:       объединить их в один кластер:

5:       для всех

6:             вычислить  по формуле Ланса-Уильямса:

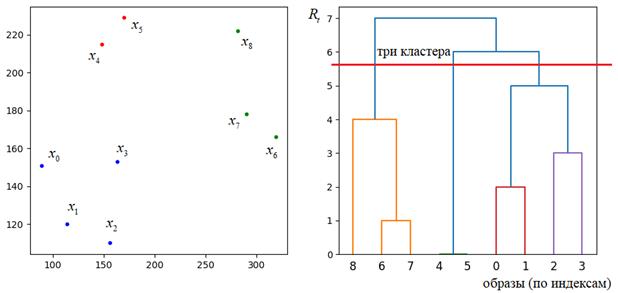
Реализовать данный алгоритм на языке Python с помощью пакета SkLearn можно, следующим образом:

machine_learning_35.py

Здесь создается объект класса AgglomerativeClustering:

clustering = AgglomerativeClustering(n_clusters=NC, linkage="ward", metric="euclidean")

которому передается число итоговых (выходных) кластеров, способ вычисления расстояний между кластерами и метрика для исходных данных (объектов). А, затем, алгоритм применяется ко входным данным:

x_pr = clustering.fit_predict(x)

На выходе получаем NumPy массив из набора объектов, сгруппированных по кластерам.

Подробную документацию по этим и другим параметрам можно почитать на странице официальной документации:

https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html

Дендрограмма

Для визуализации процесса иерархической кластеризации и оценки ее качества часто строят график специального вида, который получил название дендрограмма.

По вертикали откладывается минимальное расстояние  между кластерами, а по горизонтали – исходные данные (объекты). Глядя на этот график, мы сразу видим, в каком порядке происходило объединение данных в группы и насколько сильно кластеры отделены друг от друга по минимальному расстоянию.

Хороший алгоритм иерархической кластеризации должен давать дендрограмму без внутренних пересечений и с ярко выраженными минимальными отступами между формируемыми кластерами. Дендрограмма на рисунке соответствует этим критериям. Конечно, при выборе других метрик и способов вычисления расстояний между кластерами, дендрограмма будет меняться.

Кроме оценки качества этот график показывает нам, где можно провести уровень отсечения для получения определенного числа выходных кластеров. Это очень удобно, особенно, если мы наперед не знаем, на сколько таксонов следует разбить входные данные. Дендрограмма может помочь увидеть явные различия между разными группами на разных уровнях иерархии.

Итак, общее заключение здесь можно сделать, следующее:

• дендрограмма должна иметь монотонный характер (не иметь внутренних пересечений), то есть, расстояния между объединяемыми кластерами должны постоянно увеличиваться:

  

  Существует теорема (Миллиган, 1979 г.), которая утверждает, что дендрограмма будет монотонной, если коэффициенты в формуле Ланса-Уильямса подчиняются, следующим условиям:

  

• при сжимающем расстоянии:  (когда на каждой последующей итерации расстояния между центрами кластеров уменьшаются), мы будем получать внизу дендрограммы разреженные кластеры, а выше к корню – более густые;
• при растягивающем расстоянии , наоборот, внизу будут образовываться густые кластеры, а выше к корню – более разреженные (обычно стремятся к растягивающему расстоянию, т.к. это хорошо согласуется с представлением правильной работы алгоритмов кластеризации).

Рекомендации по агломеративной иерархической кластеризации

1. При выборе метрики расстояний между кластерами лучше начать с расстояния Уорда (Ward), а затем пробовать другие, например, часто следующим берут расстояние дальнего соседа.

2. Строят несколько вариантов кластеризаций (с разными метриками) и по дендрограмме выбирают лучший вариант (чисто визуально).

3. Результирующее число кластеров определяют по уровню, где максимально изменение минимального расстояния .

Практический курс по ML: https://stepik.org/course/209247/

Видео по теме

Машинное обучение. Начало

#1. Что такое машинное обучение? Обучающая выборка и признаковое пространство

#2. Постановка задачи машинного обучения

#3. Линейная модель. Понятие переобучения

#4. Способы оценивания степени переобучения моделей

#5. Уравнение гиперплоскости в задачах бинарной классификации

#6. Решение простой задачи бинарной классификации

#7. Функции потерь в задачах линейной бинарной классификации

#8. Стохастический градиентный спуск SGD и алгоритм SAG

#9. Пример использования SGD при бинарной классификации образов

#10. Оптимизаторы градиентных алгоритмов: RMSProp, AdaDelta, Adam, Nadam

#11. L2-регуляризатор. Математическое обоснование и пример работы

#12. L1-регуляризатор. Отличия между L1- и L2-регуляризаторами

#13. Логистическая регрессия. Вероятностный взгляд на машинное обучение

#14. Вероятностный взгляд на L1 и L2-регуляризаторы

#15. Формула Байеса при решении конкретных задач

#16. Байесовский вывод. Наивная байесовская классификация

#17. Гауссовский байесовский классификатор

#18. Линейный дискриминант Фишера

#19. Введение в метод опорных векторов (SVM)

#20. Реализация метода опорных векторов (SVM)

#21. Метод опорных векторов (SVM) с нелинейными ядрами

#22. Вероятностная оценка качества моделей

#23. Показатели precision и recall. F-мера

#24. Метрики качества ранжирования. ROC-кривая

#25. Метод главных компонент (Principal Component Analysis)

#26. Сокращение размерности признакового пространства с помощью PCA

#27. Сингулярное разложение и его связь с PCA

#28. Многоклассовая классификация. Методы one-vs-all и all-vs-all

#29. Метрические методы классификации. Метод k ближайших соседей

#30. Методы парзеновского окна и потенциальных функций

#31. Метрические регрессионные методы. Формула Надарая-Ватсона

#32. Задачи кластеризации. Постановка задачи

#33. Алгоритм кластеризации Ллойда (K-средних, K-means)

#34. Алгоритм кластеризации DBSCAN

#35. Агломеративная иерархическая кластеризация. Дендограмма

#36. Логические методы классификации

#37. Критерии качества для построения решающих деревьев

#38. Построение решающих деревьев жадным алгоритмом ID3

#39. Усечение (prunning) дерева, обработка пропусков и категориальных признаков

#40. Решающие деревья в задачах регрессии. Алгоритм CART

#41. Случайные деревья и случайный лес. Бутстрэп и бэггинг

#42. Введение в бустинг (boosting). Алгоритм AdaBoost при классификации

#43. Алгоритм AdaBoost в задачах регрессии

#44. Градиентный бустинг и стохастический градиентный бустинг

#45. Нейронные сети. Краткое введение в теорию

#46. Обучение нейронной сети. Алгоритм back propagation