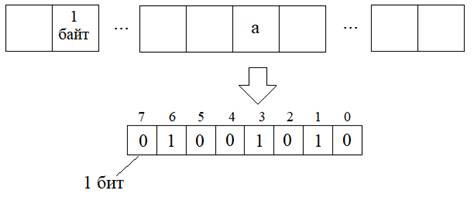
Битовые операции И, ИЛИ, НЕ, XOR

Смотреть материал на видео

В языке Java можно выполнять операции над отдельными битами переменных. Для тех кто не знает, краткий экскурс в биты. Смотрите, например, когда мы в программе задаем вот такую переменную 

byte a;

то где-то в памяти компьютера выделяется один байт памяти. Байт – это наименьшая неделимая ячейка памяти. Вся память компьютера поделена на байты. Условно это можно изобразить так

В свою очередь байт состоит из 8 бит. Бит – это элементарная ячейка памяти, которая может принимать только два значения: 0 и 1. И каждый бит имеет свой номер от младшего 0 – до старшего 7. Так вот, все целочисленные значения переменной a можно представить в виде последовательности из 8 бит. Например, значение, что изображено на рисунке соответствует десятичному числу

А общее число вариантов равно

Именно поэтому переменная типа byte может содержать числа

от -128 до 127

всего 256 вариантов. Причем признаком отрицательного числа является старший бит, установленный в 1. Например, вот такое число в битовом представлении

10000000

чему равно? Для этого нам надо инвертировать вот эти младшие 7 бит, вычислить его десятичное представление и прибавить 1. Получим:

1111111 = 127+1

значит, это отрицательное число -128. А вот если взять такое:

11111111

то после инверсии 7 младших бит, имеем:

0000000 = 0+1

значит, это число -1. Вот так кодируются отрицательные числа на уровне бит. И это работает не только в Java – это общепринятая кодировка чисел через биты.

Итак, язык Java имеет операторы, позволяющие менять отдельные биты переменных. Основными из них являются:

И, ИЛИ, НЕ, исключающее ИЛИ (XOR)

Битовая операция НЕ

Начнем с самой простой битовой операции НЕ, которая выполняет инверсию бит в соответствии с такой табличкой:

x

НЕ

0

1

1

0

На языке Java она записывается как ~ тильда. И приведем такую программу. 

int var = 121;  //двоичный вид: 00000000 00000000 00000000 01111001
int not_v = ~var; //результат:  11111111 11111111 11111111 10000110 (число -122)
 
System.out.println(not_v);

Здесь мы сначала задаем переменную var со значением 121, затем, выполняем ее побитовую инверсию, и выводим результат на экран.

Запустим программу и видим на экране число -122, что и должно быть, так как инверсия последних 7 бит дает

1111001 = 121+1

значит, это число -122.

Битовая операция И

Далее рассмотрим операцию поразрядное И. На Java она записывается как & и для ее работы нужны уже два числа или две переменные, например, так. 

byte flags = 5;  //двоичный вид:  00000101
byte mask = 4; //двоичный вид:  00000100
 
int res = flags&mask;
 
System.out.println(res);

В этой программе происходит побитовое умножение соответствующих бит двух переменных в соответствии вот с такой таблицей истинности:

x

y

И

0

0

0

0

1

0

1

0

0

1

1

1

flags=

0

0

0

0

0

1

0

1

mask=

0

0

0

0

0

1

0

0

res =

0

0

0

0

0

1

0

0

то есть, смотрите что получается. В соответствии с таблицей истинности результирующие биты будут следующими. (перечислить). В итоге, переменная res будет равна 4. Запустим программу и убедимся, что это так.

Ну хорошо, разобрались, но зачем все это надо? Смотрите, если нам нужно проверить включен ли какой-либо бит числа (то есть установлен в 1), то мы можем это сделать с помощью битовой операции И следующим образом: 

byte flags = 5;  //двоичный вид:  00000101
byte mask = 4;   //двоичный вид:  00000100
 
if ( (flags&mask) == mask) System.out.println("Включен 2-й бит числа");
else System.out.println("2-й бит выключен");

Для проверки мы здесь использовали оператор if, о котором подробно поговорим на следующем занятии. Интерпретировать здесь его следует так: если вот эта битовая операция по числовому значению будет равна mask, то выполняется вот эта конструкция, иначе – вот эта.

И теперь смотрите, мы здесь задали маску, у которой 2-й бит установлен в 1. Тогда в соответствии с операцией И у нас в результате все биты обнулятся, кроме 2-го, но только в том случае, если в переменной flags он установлен в 1. Давайте запустим программу и убедимся, что все работает.

И для проверки поменяем переменную flags на 1 

byte flags = 1;  //двоичный вид:  00000001

и проверим что будет. Да, все верно, выводится что 2-й бит выключен. Вот так мы проверили включен или нет 2-й бит. По аналогии можно проверять и другие биты или сразу группы бит.

Другим важным назначением операции И является выключение определенных бит переменной. Это делается так. 

byte flags = 13;  //двоичный вид:  00001101
byte mask = 5;   //двоичный вид:  00000101
 
flags = (byte)(flags & ~mask);  //двоичная запись 00001000
System.out.println(flags);

Что происходит здесь? Сначала выполняется инверсия бит маски, так как операция НЕ имеет более высокий приоритет, чем операция И. Получаем, что маска состоит из вот таких бит. Затем, идет операция поразрядное И, и там где в маске стоят 1 биты переменной flags не меняются, остаются прежними, а там где стоят в маске 0 – эти биты в переменной flags тоже становятся равными 0. За счет этого происходит выключение 2-го и 0-го битов переменной flags.

flags=

0

0

0

0

1

1

0

1

mask=

1

1

1

1

1

0

1

0

flags=

0

0

0

0

1

0

0

0

Кстати, вот эту строчку можно переписать короче: 

flags &= ~mask;    //двоичная запись 00001000

Это будет одно и то же.

Битовая операция ИЛИ

Следующая битовая операция – поразрядное ИЛИ. Она задается оператором | и ее таблица истинности выглядит следующим образом.

x

y

ИЛИ

0

0

0

0

1

1

1

0

1

1

1

1

Где обычно используется эта операция? Обычно ее применяют, когда нужно включить отдельные биты переменной. Рассмотрим такую программу. 

byte flags = 8;  //двоичный вид:  00001000
byte mask = 5;   //двоичный вид:  00000101
 
flags = (byte)(flags | mask);   //двоичная запись 00001101 (число 13)
 
System.out.println(flags);

Здесь мы имеем такую картину.

flags=

0

0

0

0

1

0

0

0

mask=

0

0

0

0

0

1

0

1

flags=

0

0

0

0

1

1

0

1

то есть, операция поразрядное ИЛИ, как бы собирает все единички из обеих переменных и получается такое своеобразное сложение. Кстати, в этом случае действительно получилось 8+5=13. Но это будет не всегда так, например, если 

byte flags = 9;  //двоичный вид:  00001001

то результат тоже будет 13, так как операция ИЛИ включает бит вне зависимости был ли он уже включен или нет, все равно на выходе будет единица. И здесь уже 9+5=13, что математически неверно.

Битовая операция исключающее ИЛИ (XOR)

И последняя базовая операция работы с битами – исключающее ИЛИ (ее еще называют XOR). Она задается оператором ^ и имеет такую таблицу истинности:

x

y

XOR

0

0

0

0

1

1

1

0

1

1

1

0

Из нее видно, что данная операция позволяет переключать биты числа, то есть, если они были равны 0, то станут 1 и, наоборот, если были 1 – станут 0. Продемонстрируем это на таком примере. 

byte flags = 9;  //двоичный вид:  00001001
byte mask = 1;   //двоичный вид:  00000001
 
flags = (byte)(flags ^ mask);     //двоичная запись 00001000 (число 8)
System.out.println(flags);
 
flags ^= mask;    //двоичная запись 00001001 (число 9)
System.out.println(flags);

flags=

0

0

0

0

1

0

0

1

mask=

0

0

0

0

0

0

0

1

flags=

0

0

0

0

1

0

0

0

Интересной особенностью операции XOR является отсутствие потерь данных при ее работе. Что это значит? Смотрите, какую бы маску мы не взяли, дважды примененная маска дает исходное число. 

byte flags = 9;    //двоичный вид:  00001001
byte mask = 111;   //двоичный вид:  01101111
 
System.out.println(flags);
 
flags ^= mask;    //двоичная запись 01100110 (число 102)
System.out.println(flags);
 
flags ^= mask;    //двоичная запись 00001001 (число 9)
System.out.println(flags);

Это связано с эффектом переключения бит, а значит, двойное переключение даст исходный результат. Где этот эффект можно применить? Самое простое – в шифровании данных. Например, у нас есть сообщение в виде строки, и маска – как шифровальный ключ. 

String msg = "Привет мир!";
byte key = 111;
 
System.out.println(msg);
 
char[] str = msg.toCharArray();
for(int i=0;i < msg.length();++i)
    str[i] ^= key;
 
msg = new String(str);
System.out.println(msg);
 
for(int i=0;i < msg.length();++i)
    str[i] ^= key;
 
msg = new String(str);
System.out.println(msg);

В частности по такому принципу устроена защита по паролю в архиваторе zip. Причем, сам пароль является ключом, который накладывается по XOR на заархивированные данные.

Вот мы с вами рассмотрели основные битовые операции, и обратите внимание, что все их можно записывать в таком виде:

Начальная форма

Краткая форма

Приоритет

a = a & b;

a &= b;

2 (И)

a = a | b;

a |= b;

1 (ИЛИ)

a = a ^ b;

a ^= b;

1 (XOR)

~a;

3 (НЕ)

Операторы смещения бит

И в заключение занятия рассмотрим еще два распространенных битовых оператора

>> смещение бит вправо
<< смещение бит влево 

int x = 160;       // 10100000
System.out.println(x);
x = x >> 1;                // 01010000 (число 80)
System.out.println(x);
x = x >> 1;                // 00101000 (число 40)
System.out.println(x);
x = x >> 1;                // 00010100 (число 20)
System.out.println(x);
x = x >> 1;                // 00010100 (число 10)
System.out.println(x);
x = x >> 1;                // 00010100 (число 5)
System.out.println(x);
x = x >> 1;                // 00010100 (число 2)
System.out.println(x);
x = x >> 1;                // 00010100 (число 1)
System.out.println(x);

Смотрите, что здесь получается. Мы перед каждым выводом переменной x сдвигаем ее биты на 1 вправо. В результате получаются вот такие десятичные числа. Заметили закономерность? Да, это целочисленное деление числа на 2. Почему целочисленное? Обратите внимание после 5 идет 2 – это как раз результат целочисленного деления 5/2=2 (как мы говорили на четвертом занятии когда проходили арифметические операции).

Если же мы будем сдвигать все на два бита 

int x = 160;       // 10100000
System.out.println(x);
x = x >> 2;                // 00101000 (число 40)
System.out.println(x);

то получим число 40, то есть, 160:4 = 40 – это эквивалент целочисленного деления на 4. То есть, получается, что операция сдвига вправо на n бит дает целочисленное деление на .

По аналогии работает и операция сдвига бит влево. 

byte x = 5;    // 00000101
System.out.println(x);
x = (byte)(x << 1);                // 00001010 (число 10)
System.out.println(x);

Только здесь получается эффект умножения на 2. Или при сдвиге на n бит влево, получим умножение на . Причем эти операции умножения и деления работают значительно быстрее, чем традиционные арифметические операции умножения и деления. Поэтому, разработчики различных алгоритмов для маломощных компьютеров стараются составить вычисления так, чтобы они базировались на сдвиговых операциях, исключая прямое умножение и деление.

Видео по теме

#1 Установка пакетов и первый запуск программы

#2 Структура программы, переменные, константы, оператор присваивания

#3 Консольный ввод/вывод, импорт пакетов

#4 Арифметические операции

#5 Условные операторы if и switch

#6 Операторы циклов while, for, do while

#7 Массивы, обработка элементов массива

#8 (часть 1) Строки в Java, методы класса String

#8 (часть 2) Строки - классы StringBuffer и StringBuider

#9 Битовые операции И, ИЛИ, НЕ, XOR

#10 Методы, их перегрузка и рекурсия