|
Расставляем корабли в игре Морской бойАрхив проекта: ga_8.zip На этом занятии мы рассмотрим еще один пример использования генетического алгоритма для расстановки кораблей в игре «Морской бой». Наша цель разместить один четырехпалубный, два трехпалубных, три двухпалубных и четыре однопалубных кораблей на игровом поле так, чтобы они не соприкасались между собой:
Вначале нам нужно определиться с форматом данных в хромосомах. Я закодировал их, следующим образом:
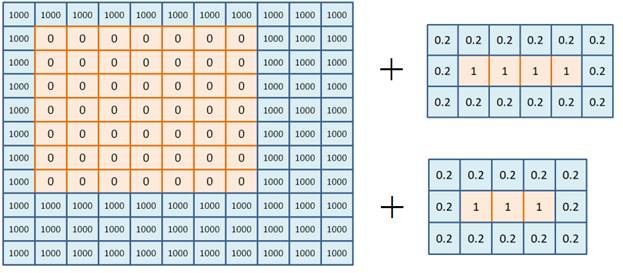
Здесь x, y – положение корабля (целое число от 1 до 10); p – ориентация корабля (0 – по горизонтали; 1 – по вертикали). Общая длина хромосомы составляет 10*3 = 30 генов. Идея вычисления приспособленности особиСледующим важным шагом является вычисление значения функции приспособленности каждого индивидуума. Идея расчета в нашем алгоритме будет следующей. Вначале сформируем матрицу, в которой нули будут описывать игровое поле, а граничные значения 1000 – величину штрафа за расположение корабля за пределами игрового поля:
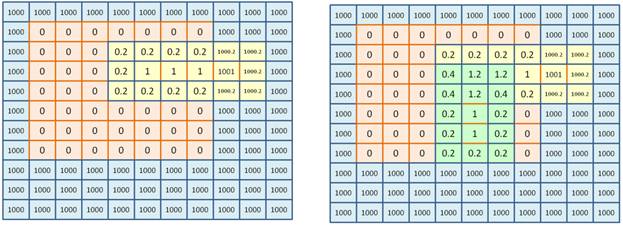
Например, добавляя маску для четырехпалубного корабля, расположенного так, как показано на рисунке ниже, мы получим значения в пределах игрового поля не более единицы, а за его пределами – более 1000:
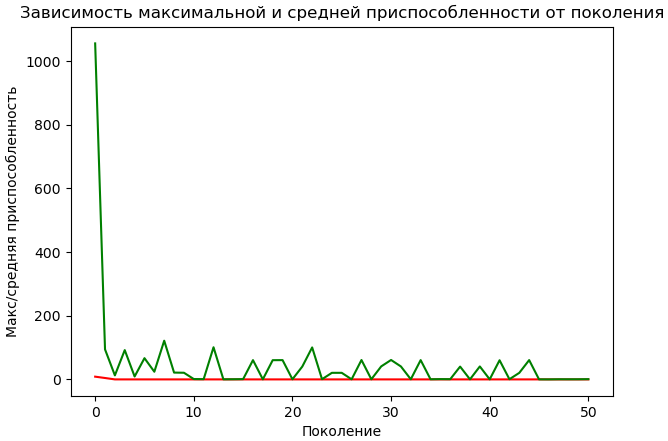
Если, затем, добавить трехпалубный корабль с наложением на четырехпалубный, то в области игрового поля будем получать величины больше единицы (см. второй рисунок). Таким образом, логика вычисления значения приспособленности особи, следующая. В игровой области суммируем все величины больше 1, а за его пределами – все значения более 1000. Общая сумма и будет определять приспособленность индивидуума. Можно заметить, если корабли располагаются по правилам игры, то значение приспособленности равно нулю. И возрастает, при увеличении числа ошибочных расстановок. То есть, в процессе оптимизации нам нужно будет минимизировать функцию принадлежности. Реализация алгоритма на PythonДавайте теперь реализуем этот алгоритм на Python с использованием пакета DEAP. Вначале выполним импорт необходимых пакетов и модулей: from deap import base, algorithms from deap import creator from deap import tools import algelitism from graph_show import show_graph import random import matplotlib.pyplot as plt import numpy as np Затем, определим глобальные параметры алгоритма и задачи: POLE_SIZE = 10 SHIPS = 10 LENGTH_CHROM = 3*SHIPS # длина хромосомы, подлежащей оптимизации # константы генетического алгоритма POPULATION_SIZE = 50 # количество индивидуумов в популяции P_CROSSOVER = 0.9 # вероятность скрещивания P_MUTATION = 0.2 # вероятность мутации индивидуума MAX_GENERATIONS = 50 # максимальное количество поколений HALL_OF_FAME_SIZE = 1 hof = tools.HallOfFame(HALL_OF_FAME_SIZE) RANDOM_SEED = 42 random.seed(RANDOM_SEED) Следующим шагом определим класс FitnessMin для работы со значением приспособленности и класс Individual представления индивидуумов в популяции: creator.create("FitnessMin", base.Fitness, weights=(-1.0,)) creator.create("Individual", list, fitness=creator.FitnessMin) Здесь все стандартно и вес определен как -1, означающий, что нас будет интересовать минимум функции приспособленности. Затем, определим функцию randomShip, которая будет создавать начальных индивидуумов со случайными значениями генов: def randomShip(total): ships = [] for n in range(total): ships.extend([random.randint(1, POLE_SIZE), random.randint(1, POLE_SIZE), random.randint(0, 1)]) return creator.Individual(ships) Параметр total – это общее число кораблей. В цикле для каждого корабля создаются три случайных значения: координаты x, y и ориентация p. Далее, мы регистрируем функцию randomShip для создания индивидуума, функцию populationCreator – для создания популяции и создаем начальную популяцию размером POPULATION_SIZE: toolbox = base.Toolbox() toolbox.register("randomShip", randomShip, SHIPS) toolbox.register("populationCreator", tools.initRepeat, list, toolbox.randomShip) population = toolbox.populationCreator(n=POPULATION_SIZE) Самое сложное в этом алгоритме оказалось реализовать вычисление значения приспособленности особи. У меня получилась вот такая функция с применением списков пакета numpy: def shipsFitness(individual): type_ship = [4, 3, 3, 2, 2, 2, 1, 1, 1, 1] inf = 1000 P0 = np.zeros((POLE_SIZE, POLE_SIZE)) P = np.ones((POLE_SIZE+6, POLE_SIZE+6))*inf P[1:POLE_SIZE+1, 1:POLE_SIZE+1] = P0 th = 0.2 h = np.ones((3, 6)) * th ship_one = np.ones((1, 4)) v = np.ones((6, 3)) * th for *ship, t in zip(*[iter(individual)] * 3, type_ship): if ship[-1] == 0: sh = np.copy(h[:, :t+2]) sh[1, 1:t+1] = ship_one[0, :t] P[ship[0] - 1:ship[0] + 2, ship[1]-1:ship[1] + t+1] += sh else: sh = np.copy(v[:t+2, :]) sh[1:t+1, 1] = ship_one[0, :t] P[ship[0]-1:ship[0] + t+1, ship[1] - 1:ship[1] + 2] += sh s = np.sum(P[np.bitwise_and(P > 1, P < inf)]) s += np.sum(P[P > inf+th*4]) return s, # кортеж В целом, здесь все просто. Сначала создаем поле P с нулевыми значениями в области размещения кораблей и величинами 1000 – за пределами игрового поля. Далее идут вспомогательные матрицы h и v для формирования масок кораблей, которые, затем, будут добавляться в игровое поле для формирования числовых значений в соответствии с идеей вычисления приспособленности особи. В цикле мы перебираем по три значения из хромосомы индивидуума и по одному значению из списка type_ship. Этот список говорит, какой тип корабля в данном случае добавляется в игровое поле. Затем, добавляем маску корабля в соответствии с его ориентацией (вертикальная или горизонтальная). После расстановки всех кораблей, мы подсчитываем сумму величин, которые больше 1 и меньше 1000 – это для ошибок в пределах игрового поля и сумму величин, которые больше 1000 + 0,2∙4 – это величина штрафа при размещении кораблей за пределами игрового поля. Общая сумма, как раз, и является значением приспособленности особи. Дальше, проще. Объявим еще одну функцию для выполнения мутации хромосомы: def mutShips(individual, indpb): for i in range(len(individual)): if random.random() < indpb: individual[i] = random.randint(0, 1) if (i+1) % 3 == 0 else random.randint(1, POLE_SIZE) return individual, Здесь координаты могут меняться случайно в пределах от 1 до 10, а ориентация принимает значение 0 или 1. Затем, регистрируем все эти функции для выполнения в главном цикле ГА пакета DEAP: toolbox.register("evaluate", shipsFitness) toolbox.register("select", tools.selTournament, tournsize=3) toolbox.register("mate", tools.cxTwoPoint) toolbox.register("mutate", mutShips, indpb=1.0/LENGTH_CHROM) stats = tools.Statistics(lambda ind: ind.fitness.values) stats.register("min", np.min) stats.register("avg", np.mean) В качестве отбора используется турнирный отбор, а в качестве скрещивания – двухточечное скрещивание. Также определен экземпляр класса Statistics для сбора статистики работы ГА. Наконец, запускаем алгоритм с помощью нашей функции eaSimpleElitism(), которая реализует принцип элитизма – сохранения лучших индивидуумов в каждом поколении. И в конце, считываем статистику, отображаем лучшего индивидуума и графики: population, logbook = algelitism.eaSimpleElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION, ngen=MAX_GENERATIONS, halloffame=hof, stats=stats, verbose=True) maxFitnessValues, meanFitnessValues = logbook.select("min", "avg") best = hof.items[0] print(best) plt.plot(maxFitnessValues, color='red') plt.plot(meanFitnessValues, color='green') plt.xlabel('Поколение') plt.ylabel('Макс/средняя приспособленность') plt.title('Зависимость максимальной и средней приспособленности от поколения') plt.show() После запуска программы увидим, следующий график:
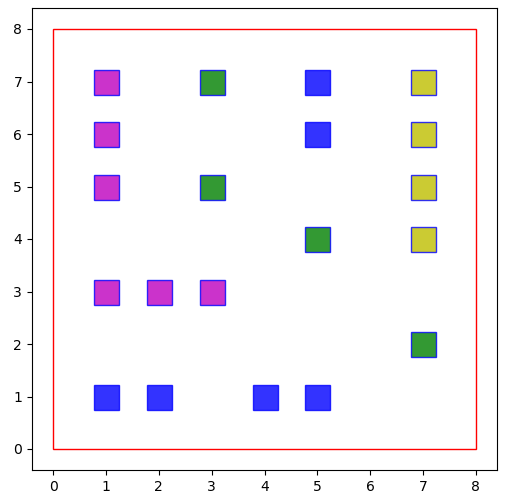
Как видим, решение находится мгновенно. И это не удивительно, так как на поле 10х10 расставить корабли очень просто. Давайте усложним задачу и уменьшим поле до размеров 7х7: POLE_SIZE = 7 Здесь лучшего решения достигнуто не было. Но, если увеличить размер популяции до 200 особей: POPULATION_SIZE = 200 то решение находится на 17-й итерации. Отображение расположения кораблейГрафики кривых – это, конечно, хорошо, но куда лучше было бы увидеть полученную расстановку. Для этого в модуль graph_show.py я добавил следующую функцию: v_ship = np.array([0, 1, 2, 3]) h_ship = np.array([0, 0, 0, 0]) type_ship=[4, 3, 3, 2, 2, 2, 1, 1, 1, 1] colors=['g', 'b', 'm', 'y'] def show_ships(ax, best, pole_size): rect = Rectangle((0, 0), pole_size+1, pole_size+1, fill=None, edgecolor='r') t_n = 0 for i in range(0, len(best), 3): x = best[i] y = best[i+1] r = best[i+2] t = type_ship[t_n] t_n += 1 if r == 1: ax.plot(v_ship[:t] + x, h_ship[:t] + y, ' sb', markersize=18, alpha=0.8, markerfacecolor=colors[t-1]) else: ax.plot(h_ship[:t] + x, v_ship[:t] + y, ' sb', markersize=18, alpha=0.8, markerfacecolor=colors[t-1]) ax.add_patch(rect) Далее, мы ее импортируем в основном модуле программы: from graph_show import show_graph, show_ships И будем вызывать на каждой итерации работы ГА, чтобы видеть лучший вариант расстановки. Вначале определим уже знакомую нам функцию: def show(ax): ax.clear() show_ships(ax, hof.items[0], POLE_SIZE) plt.draw() plt.gcf().canvas.flush_events() Включим интерактивный режим отображения данных, сформируем окно и координатные оси, а также установим размер окна и границы осей: plt.ion() fig, ax = plt.subplots() fig.set_size_inches(6, 6) ax.set_xlim(-2, POLE_SIZE+3) ax.set_ylim(-2, POLE_SIZE+3) В функции eaSimpleElitism() укажем параметр callback с функцией show и аргументом ax: population, logbook = algelitism.eaSimpleElitism(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION, ngen=MAX_GENERATIONS, halloffame=hof, stats=stats, callback=(show, (ax, )), verbose=True) После выполнения ГА выключим интерактивный режим и оставим окно с последним вариантом расстановки кораблей на экране: plt.ioff() plt.show() После выполнения программы увидим следующий конечный результат:
Конечно, это всего лишь пример того, как можно реализовать эту задачу с помощью ГА. Надеюсь, после примеров с расстановкой кораблей и определением кратчайшего маршрута в графе, вы стали лучше понимать, как конструируются генетические алгоритмы для решения тех или иных задач. Видео по теме |