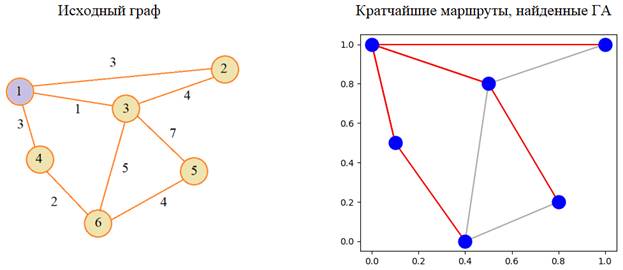
Поиск минимальных маршрутов в графеАрхив проекта: ga_6.zip На этом занятии мы с вами решим реальную практическую задачу поиска минимальных маршрутов в графе относительно выбранной вершины. Эту задачу мы уже решали с помощью алгоритма Дейкстры. Теперь сделаем то же самое, но с использованием ГА. Вот конечный результат работы этой программы (здесь кратчайшие пути определялись относительно первой вершины):
Давайте посмотрим, как это все можно реализовать на языке Python с использованием пакета DEAP. Кодирование информации в хромосомахПервым делом нам нужно формализовать задачу и определиться со способом хранения информации в хромосомах. Здесь могут быть самые разные варианты. Я выбрал следующее. Одна хромосома описывает все возможные маршруты от исходной точки (узла 1) до всех остальных вершин графа.
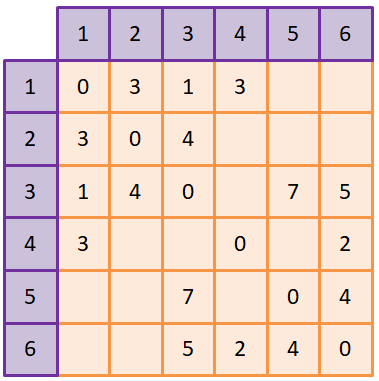
Узлы, для удобства программирования, пронумерованы от 0 до 5 (всего 6 узлов). Каждый маршрут представлен отдельным списком. Так как длина пути изначально неизвестна, то он заканчивается тогда, когда встречается вершина с номером назначения. Например, первый список определяет маршрут из 1-й вершины в 1-ю и здесь первым стоит 0. Это как раз и есть кратчайший маршрут. Второй список – это маршрут из 1-й вершины во 2-ю. И здесь сразу стоит 1. Значит, кратчайший путь из 1 в 2 – это напрямую между этими вершинами. То же самое получается для 3-й и 4-й вершин. А вот до 5-й нужно идти через вершину 3. То же самое для 6-й, здесь нужно проходить через вершину 4. Это и есть кратчайшие маршруты и вот так следует интерпретировать значения генов в хромосоме. Представление графаЧасто для описания графа пользуются матрицей смежности, которая на пересечении строк и столбцов содержит значения весов дуг между соответствующими вершинами:
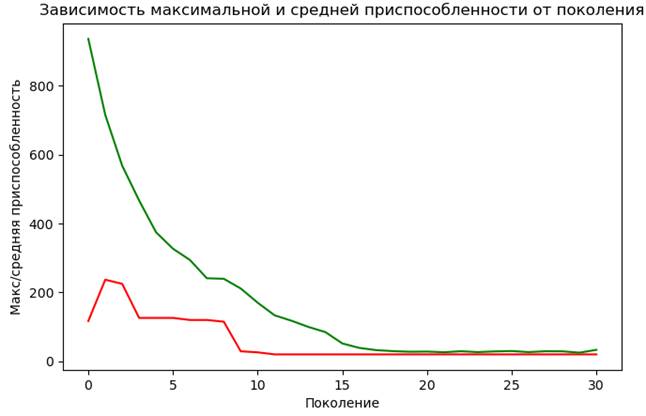
Те клетки, что не содержат значений, означают отсутствие связей. По идее, здесь можно прописать бесконечные величины, означающие бесконечно длинные маршруты. Импорт библиотек и создание индивидуумовТеперь, перейдем непосредственно к реализации ГА. Вначале выполним импорт необходимых модулей: from deap import base, algorithms from deap import creator from deap import tools import random import matplotlib.pyplot as plt import numpy as np И, затем, зададим матрицу смежности для нашего графа: inf = 100 D = ((0, 3, 1, 3, inf, inf), (3, 0, 4, inf, inf, inf), (1, 4, 0, inf, 7, 5), (3, inf, inf, 0, inf, 2), (inf, inf, 7, inf, 0, 4), (inf, inf, 5, 2, 4, 0)) Обратите внимание на величину inf. Она принимает значение 100 и означает несуществующий маршрут. То есть, когда ГА будет включать несуществующие дуги графа, то это сразу даст прибавку в 100 единиц и такой индивидуум будет заметно проигрывать тем, кто использует только допустимые дуги графа. Поэтому ГА будет стараться использовать только допустимые маршруты между узлами. Далее, мы определим необходимые константы для реализации ГА: startV = 0 # стартовая вершина LENGTH_D = len(D) LENGTH_CHROM = len(D)*len(D[0]) # длина хромосомы, подлежащей оптимизации # константы генетического алгоритма POPULATION_SIZE = 500 # количество индивидуумов в популяции P_CROSSOVER = 0.9 # вероятность скрещивания P_MUTATION = 0.1 # вероятность мутации индивидуума MAX_GENERATIONS = 30 # максимальное количество поколений И для повторяемости результатов экспериментов (работы ГА), определим «зерно» для генератора случайных чисел: RANDOM_SEED = 42 random.seed(RANDOM_SEED) После этого создадим класс FitnessMin для хранения информации о приспособленности каждого индивидуума и класс Individual, который будет представлять отдельную особь в популяции: creator.create("FitnessMin", base.Fitness, weights=(-1.0,)) creator.create("Individual", list, fitness=creator.FitnessMin) Обратите внимание, что вес (weights) определен как -1.0. Знак минус используется, когда нам нужно выполнять минимизацию функции приспособленности. Как мы с вами ранее говорили, в процессе эволюции в популяции остаются наиболее приспособленные особи, то есть, те, которые имеют наибольшее значение функции приспособленности. Указывая вес -1, мы наименьшее значение превращаем в наибольшее и, тем самым, сохраняем общую логику работы ГА. Создание начальной популяцииТеперь у нас все готово для создания начальной популяции особей в ГА. Для этого мы воспользуемся уже известным классом Toolbox и через его экземпляр (переменную toolbox) выполним регистрацию следующих функций: toolbox = base.Toolbox() toolbox.register("randomOrder", random.sample, range(LENGTH_D), LENGTH_D) toolbox.register("individualCreator", tools.initRepeat, creator.Individual, toolbox.randomOrder, LENGTH_D) toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator) Вначале регистрируется функция randomOrder, которая является алиасом стандартной функции random.sample, позволяющей генерировать случайные списки со значениями в диапазоне от 0 до LENGTH_D-1 и длиной также LENGTH_D. Причем, значения в списке формируются по возможности уникальные (без повторений), что нам и нужно. Следующая функция individualCreator создает отдельных индивидуумов на основе ранее заданного класса creator.Individual и определяет в качестве его значений объекты, которые возвращает функция toolbox.randomOrder, а число таких объектов будет LENGTH_D. В результате, у нас будет формироваться хромосома заданного формата. Наконец, третья функция populationCreator формирует обычный список, состоящий из индивидуумов. Далее, мы вызываем последнюю функцию для создания начальной популяции: population = toolbox.populationCreator(n=POPULATION_SIZE) Функции приспособленности, скрещивания и мутацииСледующим шагом в программе нужно определить, как вычислять приспособленность отдельных особей, как выполнять скрещивание и мутации. Начнем с функции приспособленности. Очевидно, она должна использовать матрицу смежности и номер стартового узла, от которого рассчитываются длины маршрутов до всех остальных вершин графа. Я ее реализовал, следующим образом: def dikstryFitness(individual): s = 0 for n, path in enumerate(individual): path = path[:path.index(n)+1] si = startV for j in path: s += D[si][j] si = j return s, # кортеж Вначале определяем переменную s, которая хранит суммарный маршрут до всех вершин графа. Далее, перебираем каждый список в хромосоме индивидуума и операцией среза выделяем только те узлы, которые относятся к текущему маршруту (метод index() у списка возвращает индекс элемента с указанным значением, его мы и берем, чтобы определить точку завершения маршрута). Далее, во вложенном (втором) цикле мы непосредственно подсчитываем длину текущего маршрута, используя значения матрицы смежности D. В конце функция должна возвратить кортеж значений. Функция скрещиванияСледующая функция cxOrdered() определяет способ скрещивания двух особей ind1 и ind2 в популяции: def cxOrdered(ind1, ind2): for p1, p2 in zip(ind1, ind2): tools.cxOrdered(p1, p2) return ind1, ind2 Она работает очень просто. В цикле перебираем пары маршрутов из первой и второй особи, а затем, вызываем встроенную функцию cxOrdered() пакета DEAP. Она реализует алгоритм упорядоченного скрещивания, о котором мы говорили на предыдущем занятии. Напомню, что данный способ скрещивания гарантирует сохранение всех индексов в хромосоме (номеров узлов графа). Это, как раз то, что нам и нужно. Функция мутацииСледующая функция mutShuffleIndexes() определяет порядок мутации генов в хромосоме. Мы здесь также перебираем списки маршрутов особи и для каждого выполняем перемешивание индексов с вероятностью indpb: def mutShuffleIndexes(individual, indpb): for ind in individual: tools.mutShuffleIndexes(ind, indpb) return individual, Для этого также используется встроенная функция mutShuffleIndexes() пакета DEAP. Регистрация функций приспособленности, отбора, скрещивания и мутацииПосле того, как все необходимые функции определены, мы должны их зарегистрировать для запуска ГА из пакета DEAP. Это делается, следующим образом: toolbox.register("evaluate", dikstryFitness) toolbox.register("select", tools.selTournament, tournsize=3) toolbox.register("mate", cxOrdered) toolbox.register("mutate", mutShuffleIndexes, indpb=1.0/LENGTH_CHROM/10) Обратите внимание на названия функций (evaluate, select, mate и mutate) они должны быть именно такими по требованию пакета DEAP. Соответственно, функция evaluate вызывается для вычисления приспособленности отдельной особи. Функция select – для формирования родителей следующего поколения. Здесь мы используем стандартную функцию selTournament() пакета DEAP, которая реализует турнирный отбор из трех случайно выбранных особей. Далее, идет функция mate для скрещивания и функция mutate – для мутации. Дополнительно у нее мы задаем indpb – вероятность мутации отдельного маршрута в хромосоме. Все, формально мы уже можем запускать ГА. Но, прежде, для сбора статистики, определим еще объект Statistics(), которая будет собирать статистику по значениям приспособленностей индивидуумов в популяции на каждой итерации работы ГА (в каждом поколении): stats = tools.Statistics(lambda ind: ind.fitness.values) stats.register("min", np.min) stats.register("avg", np.mean) В частности, мы здесь будем вычислять минимальное и среднее значения приспособленностей особей в каждом поколении. Запуск генетического алгоритмаДля запуска ГА мы воспользуемся стандартной функцией eaSimple() пакета DEAP со следующими очевидными параметрами: population, logbook = algorithms.eaSimple(population, toolbox, cxpb=P_CROSSOVER/LENGTH_D, mutpb=P_MUTATION/LENGTH_D, ngen=MAX_GENERATIONS, stats=stats, verbose=True) После этой функции выделим списки для собранной статистики: maxFitnessValues, meanFitnessValues = logbook.select("min", "avg") и отобразим графики в окне с помощью пакета matplotlib: plt.plot(maxFitnessValues, color='red') plt.plot(meanFitnessValues, color='green') plt.xlabel('Поколение') plt.ylabel('Макс/средняя приспособленность') plt.title('Зависимость максимальной и средней приспособленности от поколения') plt.show() После запуска программы увидим, следующий результат:
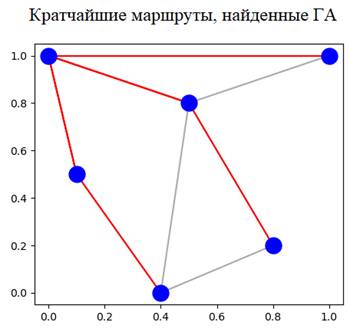
В целом, получили рабочий вариант ГА. Конечно, я заранее прописал глобальные параметры, которые приводят к хорошим результатам. Например, размер популяции 500 особей, а также хорошие вероятности скрещивания и мутации. Попробуйте самостоятельно поиграться этими параметрами и посмотрите, как ведет себя ГА при других значениях глобальных параметров. Добавление зала славыПросмотр графиков, это, конечно, хорошо, но нам бы хотелось увидеть хромосому лучшей особи. Для этого добавим в ГА объект HallOfFame() – зал славы, который будет хранить лучших индивидуумов на последней итерации. Вначале нужно создать экземпляр этого класса, например, так: HALL_OF_FAME_SIZE = 1 hof = tools.HallOfFame(HALL_OF_FAME_SIZE) Мы здесь указали, что размер «зала славы» будет состоять из одной лучшей особи. А, затем, при вызове функции algorithms.eaSimple() передать этот объект через именованный параметр halloffame: population, logbook = algorithms.eaSimple(population, toolbox, cxpb=P_CROSSOVER/LENGTH_D, mutpb=P_MUTATION/LENGTH_D, ngen=MAX_GENERATIONS, halloffame=hof, stats=stats, verbose=True) После этой функции сделаем обращение к объекту hof для получения ссылки на лучшего индивидуума: best = hof.items[0] print(best) После запуска программы в консоли увидим, следующий список: [[0, 1, 4, 3, 5, 2], [1, 4, 3, 0, 5, 2], [2, 0, 5, 1, 4, 3], [3, 2, 4, 5, 1, 0], [2, 4, 1, 5, 3, 0], [3, 5, 1, 4, 0, 2]] Это хромосома лучшей особи, которая хранит следующие списки кратчайших маршрутов:
Это соответствует оптимальному решению поставленной задачи. Отображение графа с маршрутамиВ заключение этого занятия сделаем отображение информации, записанной в хромосоме в виде графа. Для этого я создам новый файл с именем graph_show.py и размещу его в том же каталоге. А в самом файле пропишу функцию show_graph(), которая и будет выводить граф с найденными маршрутами: from matplotlib.lines import Line2D vertex = ((0, 1), (1, 1), (0.5, 0.8), (0.1, 0.5), (0.8, 0.2), (0.4, 0)) vx = [v[0] for v in vertex] vy = [v[1] for v in vertex] def show_graph(ax, best): ax.add_line(Line2D((vertex[0][0], vertex[1][0]), (vertex[0][1], vertex[1][1]), color='#aaa')) ax.add_line(Line2D((vertex[0][0], vertex[2][0]), (vertex[0][1], vertex[2][1]), color='#aaa')) ax.add_line(Line2D((vertex[0][0], vertex[3][0]), (vertex[0][1], vertex[3][1]), color='#aaa')) ax.add_line(Line2D((vertex[1][0], vertex[2][0]), (vertex[1][1], vertex[2][1]), color='#aaa')) ax.add_line(Line2D((vertex[2][0], vertex[5][0]), (vertex[2][1], vertex[5][1]), color='#aaa')) ax.add_line(Line2D((vertex[2][0], vertex[4][0]), (vertex[2][1], vertex[4][1]), color='#aaa')) ax.add_line(Line2D((vertex[3][0], vertex[5][0]), (vertex[3][1], vertex[5][1]), color='#aaa')) ax.add_line(Line2D((vertex[4][0], vertex[5][0]), (vertex[4][1], vertex[5][1]), color='#aaa')) startV = 0 for i, v in enumerate(best): if i == 0: continue prev = startV v = v[:v.index(i)+1] for j in v: ax.add_line(Line2D((vertex[prev][0], vertex[j][0]), (vertex[prev][1], vertex[j][1]), color='r')) prev = j ax.plot(vx, vy, ' ob', markersize=15) Здесь вначале импортируется необходимый класс Line2D пакета matplotlib, затем, определяется список координат вершин графа (для их отображения на графике), а также отдельные списки vx, vy координат по оси Ox и Oy. Далее, идет непосредственно функция show_graph(), которая на входе принимает объект Axis – координатные оси, в которых будет производиться рисование графа, а вторым параметром передается хромосома лучшего индивидуума. С помощью первых восьми вызовов метода add_line() производится рисование начальных связей между вершинами графа, а затем, в цикле рисуются найденные маршруты. В конце отображаются вершины графа в виде отдельных точек. Чтобы воспользоваться этой функцией в основной программе, выполним ее импорт: from graph_show import show_graph Затем, сделаем отображение сначала графиков, а потом, в отдельном окне – отображение графа с лучшим найденным решением: plt.plot(maxFitnessValues, color='red') plt.plot(meanFitnessValues, color='green') plt.xlabel('Поколение') plt.ylabel('Макс/средняя приспособленность') plt.title('Зависимость максимальной и средней приспособленности от поколения') fig, ax = plt.subplots() show_graph(ax, best) plt.show() Вот пример того, как можно формализовать задачу поиска кратчайших маршрутов, собрать статистику и отобразить результат в виде графа. Программы из этого занятия будут доступны на github и вы сможете подробно их изучить. Видео по теме |