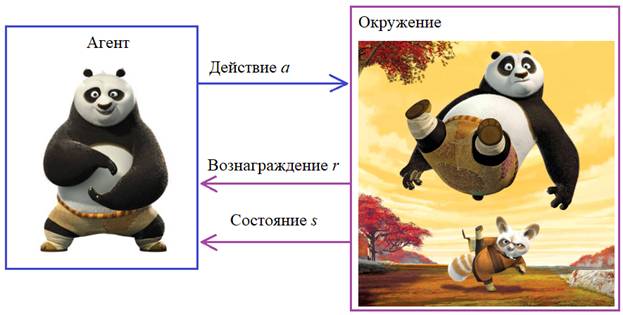
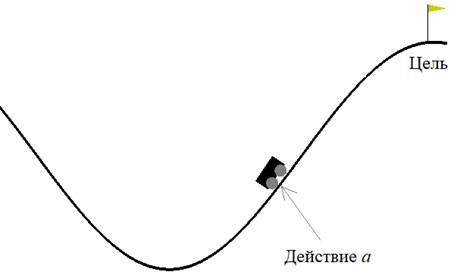
Обучение с подкреплением или как загнать машину на гору

Смотреть материал на видео

Архив проекта: ga_10.zip

Представьте, что перед нами стоит задача загнать машину на гору, но сделать это сразу не удается, так как мощности мотора не хватает. Здесь нужен разбег с соседнего склона так, чтобы по инерции забраться на правый – к флажку.

Для человека эта задача кажется естественной и относительно простой. Но как реализовать алгоритм для нахождения решения этой задачи? Как вы уже догадались – с помощью все того же генетического алгоритма. Пример с машинкой – нетривиальная математическая задача, но все что нам нужно для ГА – это уметь сравнивать приспособленности индивидуумов в популяции между собой. То есть, нам нужно вначале определиться с функцией принадлежности.

Как мы уже ранее отмечали, эта функция может быть выражена в виде алгоритма (не обязательно формулой) и это большой плюс генетических алгоритмов в отличие от многих традиционных (например, градиентного спуска), где требуется уметь вычислять значение производной от целевой функции. И в таких задачах как с машинкой определить гладкую, дифференцируемую функцию крайне сложно. Но нам это и не потребуется.

Элементы обучения с подкреплением

Машинку, которой мы управляем, назовем агентом. А среду, в которой происходит ее перемещение вместе с законами физики, - окружением. Именно в таких терминах формулируются задачи обучения с подкреплением – современного научного направления, используемое для обучения поведения игровых персонажей, управления динамическими объектами (машинами, самолетами, кораблями и т.п.). Везде, где задачу можно представить в виде агента и его взаимодействия с окружающей средой, возможно применить идею обучения с подкреплением.

На сегодняшний день разработано несколько алгоритмов такого обучения: Q-обучение, SARSA, DQN и др. Все они предполагают, что в определенные моменты времени агент может заданным образом воздействовать на среду и менять ее состояние с целью максимизации общего (долгосрочного) вознаграждения:

То есть, целью обучения агента является возможность формировать такие действия a, в зависимости от текущего состояния среды s, чтобы максимизировать суммарные (общие) вознаграждения r.

Именно так мы и будем рассматривать задачу с машинкой. В равные промежутки времени на машинку можно оказывать одно из воздействий (действие):

  • 0 – разгон влево;
  • 1 – движение по инерции;
  • 2 – разгон вправо.

Если на текущей итерации машинка не добралась до флажка, то вознаграждение будет равно r = -1. Как только машинка добирается до цели, алгоритм завершается и подсчитывается суммарное вознаграждение:

R = r1+r2+…+rN

(здесь N – это число выполненных шагов). В рамках нашей задачи ограничимся максимальным числом шагов Nmax = 200. Этого вполне достаточно, чтобы машинка забралась на правый холм. Соответственно, чем быстрее (за меньшее число итераций) агент доберется до цели, тем выше будет суммарное вознаграждение R. Фактически, эта величина и будет использоваться в качестве приспособленности особи в популяции.

Виртуальное окружение из пакета OpenAI Gym

Прежде чем реализовывать сам алгоритм, нам нужно знать, как выполнять имитацию виртуального окружения. В языке Python существует библиотека OpenAI Gym с набором виртуальных окружений для решения задач обучения с подкреплением. Подробнее о ней можно почитать на странице официальной документации:

https://gym.openai.com/docs/

Как раз с помощью OpenAI Gym мы смоделируем движение машинки между двумя холмами. Точнее, оно там уже создано и все что нужно – это установить пакет

pip install gym

и создать окружение с именем MountainCar-v0: 

env = gym.make('MountainCar-v0')

Затем, для инициализации созданной среды, следует вызвать метод reset(): 

observation = env.reset()

Этот метод возвращает объект observation (наблюдение), содержащий текущую информацию о состоянии среды. Какая именно информация входит в этот объект зависит от типа окружающей среды. В нашем случае (для MountainCar-v0) этот объект будет состоять из двух вещественных чисел: положения и текущей скорости машинки.

Далее, для воздействия на машинку виртуальной среде можно передать три команды:

  • 0 – разгон влево;
  • 1 – движение по инерции;
  • 2 – разгон вправо.

Например, так: 

observation, reward, done, info = env.step(1)

Здесь метод step() возвращает четыре объекта:

  • observation – текущую информацию об окружении после выполнения действия;
  • reward – вознаграждение за выполнение команды (обычно, возвращается значение -1 за каждую выполненную команду);
  • done – флаг (True – если цель была достигнута; False – в противном случае);
  •  info – словарь с информацией для отладки (алгоритм не должен использовать эти данные).

Для визуализации текущего состояния среды достаточно выполнить команду: 

env.render()

И в конце, после завершения работы со средой, ее следует закрыть: 

env.close()

(Конечно, она также автоматически закрывается при завершении программы).

Определение приспособленности особи

Теперь, когда у нас есть виртуальное окружение и общее понимание задачи, перейдем к реализации генетического алгоритма. Прежде всего, нужно определиться со способом кодирования информации в генах хромосом. Вполне очевидным решением здесь является хромосома, состоящая из 200 ген, и в каждом гене может быть записана одна из команд: 0, 1 или 2:

Далее, на основе этой хромосомы нужно определять ее приспособленность. Сделать это можно достаточно просто. Для каждого индивидуума мы будем запускать виртуальное окружение (без визуализации) и подсчитывать число шагов actionCounter, за которое была достигнута цель (машинка доехала до флажка). Затем, вычислять значение приспособленности по формуле:

score = 0 - (LENGTH_CHROM - actionCounter) / LENGTH_CHROM

Мы здесь берем отрицательное значение доли оставшихся шагов и чем она больше, тем более приспособлен индивид. То есть, генетический алгоритм будет стремиться минимизировать функцию приспособленности особей в популяции.

Но в самом начале вполне возможны ситуации, когда ни для одной из хромосом машинка не добирается до флажка за 200 шагов. Тогда значения приспособленностей всех индивидуумов будут равны нулю. Чтобы этого избежать, мы пропишем следующее условие: 

    if actionCounter < LENGTH_CHROM:
        score = 0 - (LENGTH_CHROM - actionCounter) / LENGTH_CHROM
    else:
        score = abs(observation[0] - FLAG_LOCATION)

Если число итераций actionCounter меньше длины хромосомы, то машинка достигла цели и вычисления происходят по ранее определенной формуле. А иначе мы просто вычисляем расстояние между машинкой и целью (флагом). Таким образом, если агент не достигает цели, то лучшей хромосомой будет считаться та, для которой машинка оказывается ближе всего к цели.

Конечно, это всего лишь пример формирования значения приспособленности особи. Вы вполне могли бы придумать другие формулы вычисления. Это элемент творческого процесса: определение приспособленностей особей в зависимости от состояния агента в окружающей среде. Каждый может реализовать это по-своему. Главное, чтобы значение функции возрастало (или убывало) для лучших решений.

Реализация ГА на Python

Давайте теперь реализуем генетический алгоритм на Python с использованием пакета DEAP. Вначале, как всегда, импортируем необходимые библиотеки: 

from deap import base, algorithms
from deap import creator
from deap import tools
 
import algelitism
 
import random
import matplotlib.pyplot as plt
import numpy as np
 
import gym

Создаем объект виртуального окружения MountainCar-v0: 

env = gym.make('MountainCar-v0')

И определяем необходимые параметры вместе с объектом «зала славы» и «зерном» генератора случайных чисел: 

LENGTH_CHROM = 200    # длина хромосомы, подлежащей оптимизации
 
# константы генетического алгоритма
POPULATION_SIZE = 50   # количество индивидуумов в популяции
P_CROSSOVER = 0.9       # вероятность скрещивания
P_MUTATION = 0.2        # вероятность мутации индивидуума
MAX_GENERATIONS = 150    # максимальное количество поколений
HALL_OF_FAME_SIZE = 3
 
hof = tools.HallOfFame(HALL_OF_FAME_SIZE)
 
RANDOM_SEED = 42
random.seed(RANDOM_SEED)

Далее, два стандартных класса для описания индивидуума в популяции со значением веса -1 – для отыскания минимума функции приспособленности: 

creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)

Затем, регистрируем функции для генерации случайных команд, создания индивидуума и всей популяции: 

toolbox = base.Toolbox()
toolbox.register("randomAction", random.randint, 0, 2)
toolbox.register("individualCreator", tools.initRepeat, creator.Individual, toolbox.randomAction, LENGTH_CHROM)
toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)
 
population = toolbox.populationCreator(n=POPULATION_SIZE)

После этого, объявим функцию для определения приспособленности конкретной особи: 

def getCarScore(individual):
    FLAG_LOCATION = 0.5
    observation = env.reset()
    actionCounter = 0
 
    for action in individual:
        actionCounter += 1
        observation, reward, done, info = env.step(action)
 
        if done:
            break
 
    if actionCounter < LENGTH_CHROM:
        score = 0 - (LENGTH_CHROM - actionCounter) / LENGTH_CHROM
    else:
        score = abs(observation[0] - FLAG_LOCATION)
 
    return score,

Здесь все так, как мы с вами только что говорили. Делается цикл по командам в хромосоме, на каждой итерации цикла увеличивается счетчик actionCounter, пока не пройдем по всей хромосоме или не будет достигнута цель. Далее, вычисляем значение приспособленности и возвращаем его в виде кортежа.

Ниже зарегистрируем функции для работы ГА в пакете DEAP, а также объект Statistics для сбора статистики: 

toolbox.register("evaluate", getCarScore)
toolbox.register("select", tools.selTournament, tournsize=2)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutUniformInt, low=0, up=2, indpb=1.0/LENGTH_CHROM)
 
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("min", np.min)
stats.register("avg", np.mean)

Запускаем ГА с помощью нашей модифицированной функции eaSimpleElitism(): 

population, logbook = algelitism.eaSimpleElitism(population, toolbox,
                                        cxpb=P_CROSSOVER,
                                        mutpb=P_MUTATION,
                                        ngen=MAX_GENERATIONS,
                                        halloffame=hof,
                                        stats=stats,
                                        verbose=True)

И отображаем статистику вместе с лучшей хромосомой: 

maxFitnessValues, meanFitnessValues = logbook.select("min", "avg")
 
best = hof.items[0]
print(best)
 
plt.plot(maxFitnessValues, color='red')
plt.plot(meanFitnessValues, color='green')
plt.xlabel('Поколение')
plt.ylabel('Макс/средняя приспособленность')
plt.title('Зависимость максимальной и средней приспособленности от поколения')
plt.show()

В самом конце запустим визуализацию движения машинки для лучшей особи: 

observation = env.reset()
 
for action in best:
    env.step(action)
    env.render()
 
env.close()

После запуска программы увидим, как машинка достигает флажка. Решение задачи ГА находит в 121-м поколении. Вы можете поиграться глобальными параметрами и, возможно, сможете получить решение за более короткое время. Здесь же, мы с вами увидели пример того, как можно формализовать и решать задачи взаимодействия агента с окружающей средой, используя генетический алгоритм.

Видео по теме

Генетический алгоритм история и возможности

#1. Основные этапы работы генетического алгоритма

#2. Делаем генетический алгоритм для задачи OneMax

#3. DEAP - пакет для создания генетических алгоритмов

#4. Как генетический алгоритм находит решения. Преимущества и недостатки

#5. Обзор методов отбора, скрещивания и мутации

#6. Поиск минимальных маршрутов в графе

#7. Делаем элитизм. Жесткие и мягкие ограничения

#8. Расставляем корабли в игре Морской бой

#9. Пример поиска минимума функции

#10. Обучение с подкреплением или как загнать машину на гору

#11. Не дай шесту упасть или как нейросеть держит баланс