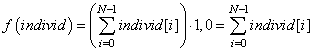|
DEAP - пакет для создания генетических алгоритмовАрхив проекта: ga_3.py На предыдущем занятии мы с вами с нуля написали первую реализацию ГА для задачи OneMax. Но это долгий путь. Я специально его привел с самого начала, чтобы вы во всех подробностях увидели работу и реализацию ГА. Теперь же сделаем следующий шаг и упростим программу с помощью пакета DEAP (сокращение от Distributed Evolutionary Algorithms in Python – распределенные эволюционные алгоритмы на Python) разработанного специально для создания реализаций ГА на Python. Подробную документацию можно посмотреть по ссылке: https://deap.readthedocs.io/en/master/ Первым делом нам нужно его установить. Делается это просто, с помощью команды: pip install deap И если все прошло в штатном режиме, то в программе будут работать три следующих импорта: from deap import base from deap import creator from deap import tools Что это такое и за что они отвечают я сейчас расскажу. Функция creator.create()Начнем с модуля creator. Он позволяет создавать новые объекты (классы) в программе. Для этого используется функция: create(<название класса>, <базовый класс>, [атрибуты нового класса]) Например, если записать: creator.create("Point", object, MAX_COORD = 10, MIN_COORD = 0, coords=list) то в ветке creator будет создан класс вида: class Point(object): MAX_COORD = 10 MIN_COORD = 0 def __init__(self): self.coords = list() Обратите внимание, все параметры, которые ссылаются на неизменяемые типы данных, прописываются как атрибуты класса Point, а изменяемые (список list) – как локальные свойства экземпляра класса Point. Это важный момент. Далее, мы можем воспользоваться этим классом, например, так: pt = creator.Point() Как использовать этот модуль в нашей программе? Смотрите, мы создавали два класса: FitnessMax и Individual. Давайте, теперь, определим их через функцию create. Первый класс запишем в виде: creator.create("FitnessMax", base.Fitness, weights=(1.0,)) Здесь мы создаем класс с именем FitnessMax, наследуя от базового класса base.Fitness, который отвечает за операции над значениями приспособленности конкретного индивида. В частности, параметр weights со значением 1.0 означает, что мы будем использовать одно число для оценки степени приспособленности особи. В действительности, конечное значение функции принадлежности будет определяться произведением:
Я напомню, что в задаче OneMax значение принадлежности индивида определяется как сумма значений его генов:
И в нашем случае, имеем одно число values[0] и один вес weights[0], то есть, итоговое значение функции принадлежности, будет равно:
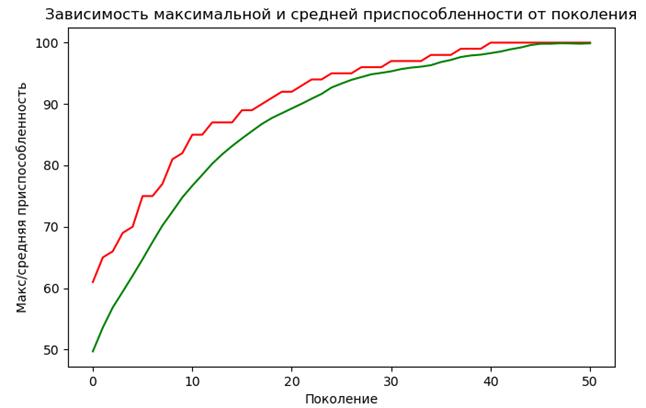
Кстати, если бы нам нужно было минимизировать значение values при решении нашей задачи, то достаточно было бы прописать вес: weights=(-1.0,) Вот в этом роль данного параметра. Следующей строчкой мы создадим класс Individual, который наследуется от класса list и имеет одно локальное свойство fitness: creator.create("Individual", list, fitness=creator.FitnessMax) Обратите внимание, мы обращаемся к ранее созданному классу FitnessMax, указывая пространство имен creator, где он находится. Так как класс FitnessMax воспринимается как изменяемый объект, то fitness станет локальным свойством экземпляра класса Individual и мы получим то же самое его представление, что и ранее. Метод toolbox.register()Далее по программе у нас с вами определено несколько вспомогательных функций. Пакет DEAP позволяет упростить и этот момент. Для этого мы воспользуемся классом: base.Toolbox и модулем: tools Вначале я покажу принцип использования этого инструмента. Предположим, что у нас есть простая функция для вычисления суммы двух величин: def sum_two(a, b): return a+b Тогда, с помощью экземпляра класса base.Toolbox(): toolbox = base.Toolbox() можно зарегистрировать псевдоним этой функции, следующим образом: toolbox.register("sum_alias", sum_two) и воспользоваться ей через это второе имя: res = toolbox. sum_alias(5, 2) Здесь мы не получаем особо никакого дополнительного эффекта. Но можно зарегистрировать псевдоним и так, указывая, что второй параметр b по умолчанию принимает значение 2: toolbox.register("sum_2", sum_two, b = 2) Тогда, вызов функции: res = toolbox.sum_2(5) будет аналогичен предыдущему и даст то же значение res = 7. Именно эти дополнительные параметры, которые можно указывать для алиаса функции и делают инструмент toolbox полезным при разработке генетических алгоритмов. Функцию oneMaxFitness мы оставим без изменения: def oneMaxFitness(individual): return sum(individual), # кортеж А далее, создадим экземпляр класса base.Toolbox и создадим псевдоним функции random.randint, которая бы генерировала случайные значения 0 или 1: toolbox = base.Toolbox() toolbox.register("zeroOrOne", random.randint, 0, 1) То есть, смотрите, мы можем здесь взять любую стандартную функцию и прописать нужное нам поведение, указывая соответствующие параметры. Это очень удобно. Следующим шагом определим функцию для генерации списка (хромосомы), состоящего из нулей и единиц: toolbox.register("individualCreator", tools.initRepeat, creator.Individual, toolbox.zeroOrOne, ONE_MAX_LENGTH) Здесь мы используем существующую функцию initRepeat из модуля tools, которая как раз и разработана для формирования списков. В данном случае, мы ей указываем: tools.initRepeat(<контейнер для хранения генов>, <функция генерации значения гена>, <число генов в хромосоме>) То есть, на выходе функция individualCreator будет выдавать экземпляр класса creator.Individual (фактически, список), заполненный случайными величинами 0 или 1 с длиной хромосомы (списка) ONE_MAX_LENGTH. И это, практически, повторяет работу нашей прежней функции с тем же названием individualCreator(). Похожим образом пропишем алиас функции для генерации популяции, но укажем только первые два параметра: итерированный объект в виде обычного списка и элемент этого списка в виде класса toolbox.individualCreator: toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator) Теперь, мы можем создать популяцию заданного размера, просто вызвав функцию populationCreator с параметром n – размера популяции: population = toolbox.populationCreator(n=POPULATION_SIZE) Далее, вместо прежних наших функций clone(), selTournament(), cxOnePoint() и mutFlipBit() воспользуемся аналогичными встроенными функциями из модуля tools: toolbox.register("select", tools.selTournament, tournsize=3) toolbox.register("mate", tools.cxOnePoint) toolbox.register("mutate", tools.mutFlipBit, indpb=1.0/ONE_MAX_LENGTH) Обратите внимание, название алиасов (псевдонимов) этих функций лучше записывать именно в таком виде: select, mate и mutate, так как эти имена, затем, используются функциями пакета DEAP при работе ГА. Также необходимо зарегистрировать функцию с именем evaluate, которая должна возвращать кортеж значений приспособленности каждого отдельного индивида: toolbox.register("evaluate", oneMaxFitness) Опять же, функция должна иметь именно такое название, а функция oneMaxFitness() возвращать кортеж значений, даже если это одно число. Это требование пакета DEAP. Запуск ГА через функцию eaSimple()В принципе, у нас все готово для запуска ГА. Для этого мы воспользуемся готовой функцией eaSimple() модуля algorithms, который вначале также импортируем: from deap import base, algorithms population, logbook = algorithms.eaSimple(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION, ngen=MAX_GENERATIONS, verbose=True) В качестве параметров мы передаем начальную популяцию, набор объявленных функций модуля toolbox, затем, указываем вероятности для операции скрещивания и мутации, далее определяем остановку алгоритма как достижение максимального числа поколений MAX_GENERATIONS, а последний параметр verbose=True означает выводить служебную информацию на каждой итерации работы алгоритма. На выходе эта функция дает конечную популяцию и служебную информацию в виде объекта logbook. Но если сейчас запустить программу, то конечного результата в виде графиков мы не увидим. Чтобы исправить этот момент, создадим экземпляр специального класса Statistics() и в качестве аргумента передадим ссылку на функцию (в данном случае лямбда-функцию), которая укажет возвращаемую информацию для каждого конкретного индивидуума популяции: stats = tools.Statistics(lambda ind: ind.fitness.values) А, затем, в экземпляре этого класса зарегистрируем две функции для выбора максимальной и средней приспособленности особей популяции на каждой итерации работы алгоритма: stats.register("max", np.max) stats.register("avg", np.mean) Далее, в функции eaSimple() дополнительно укажем параметр stats=stats: population, logbook = algorithms.eaSimple(population, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION, ngen=MAX_GENERATIONS, stats=stats, verbose=True) И воспользуемся объектом logbook, из которого выберем поля max и avg: maxFitnessValues, meanFitnessValues = logbook.select("max", "avg") Отобразим полученные данные на графике: plt.plot(maxFitnessValues, color='red') plt.plot(meanFitnessValues, color='green') plt.xlabel('Поколение') plt.ylabel('Макс/средняя приспособленность') plt.title('Зависимость максимальной и средней приспособленности от поколения') plt.show() И увидим следующие кривые:
То есть, генетический алгоритм полностью отработал и нашел искомое решение из всех единиц. При этом программа заметно сократилась и воспринимается гораздо проще. Видео по теме |