L-система для дракона Хартера-Хайтвея, ковра Серпинского и кривой Гильберта

Архив проекта: 4_fractals.py

На этом занятии мы усовершенствуем L-систему, разработанную на прошлом занятии (если вы его не смотрели, то ссылка будет под этим видео). Здесь же мы увидим, как можно создавать более сложные аксиомы и правила на примере некоторых известных фракталов.

Вначале давайте попробуем построить фрактал под названием «дракон Хартера-Хайтвея». Аксиома представляет собой простую горизонтальную прямую линию:

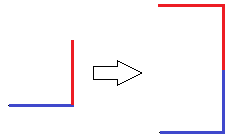
На первой итерации эта линия заменяется ломаной в виде прямого угла:

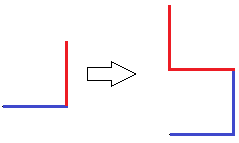
Тогда на второй итерации мы должны ожидать построение вида:

Но в действительности для второй ломаной (чтобы получить дракона) требуется выполнить инверсию:

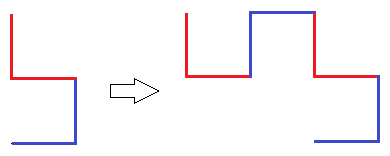
На третьем шаге все то же самое, сначала обычный уголок, потом инвертированный, затем, опять обычный, в конце – инвертированный:

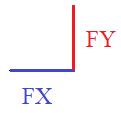
И так далее. Как реализовать такую операцию с помощью нашей L-системы не меняя ее? Сделаем одну маленькую хитрость. Линейные сегменты, которые нужно заменять обычным уголком будем обозначать через FX, а линейные сегменты для инвертированных уголков – через FY:

Что означают эти дополнительные символы X и Y? И как черепашке их интерпретировать? На самом деле черепашка может «расслабиться», так как эти символы для нее не имеют никакого значения и она должна их просто игнорировать. А вот в правилах мы их учтем, следующим образом:

"FX" → "FX+FY+"

"FY" → "-FX-FY"

Смотрите, первое правило указывает заменять сегмент FX обычным уголком. Причем, после его рисования черепашка поворачивается влево на 90 градусов (здесь угол поворота составляет 90 градусов). А правило для FY говорит, чтобы мы нарисовали уголок, но с поворотами направо, то есть, инвертированный угол. В результате, благодаря введению дополнительных символов X и Y мы как бы «помечаем» линейные сегменты, которые на следующей итерации нужно заменять или обычным или инвертированным уголком. Причем, правила подобраны так, чтобы на каждой новой итерации шло четкое чередование сегментов FX и FY.

Давайте посмотрим, как все это будет работать. Воспользуемся программой из прошлого занятия и пропишем аксиому и правила для генерации фрактала «Дракона»:

t = turtle.Turtle()
t.ht()          # скрываем черепашку
 
pen_width = 2   # толщина линии рисования (в пикселах)
f_len = 5       # длина одного сегмента прямой (в пикселах)
angle = 90      # фиксированный угол поворота (в градусах)
axiom = "FX"
 
l_sys = LSystem2D(t, axiom, pen_width, f_len, angle)
l_sys.add_rules(("FX", "FX+FY+"), ("FY", "-FX-FY"))
l_sys.generate_path(10)
l_sys.draw_turtle( (0, 0), 0)

На выходе получим следующее изображение:

Как видите, наша L-система способна и на такие «чудеса». С помощью такого же подхода к построению правил можно сгенерировать другой известный фрактал под названием «ковер Серпинского»:

angle = 60      # фиксированный угол поворота (в градусах)
axiom = "FXF--FF--FF"
 
l_sys = LSystem2D(t, axiom, pen_width, f_len, angle)
l_sys.add_rules(("F", "FF"), ("X", "--FXF++FXF++FXF--"))
l_sys.generate_path(5)
l_sys.draw_turtle( (0, 0), 0)

Или кривую Гильберта:

angle = 90      # фиксированный угол поворота (в градусах)
axiom = "X"
 
l_sys = LSystem2D(t, axiom, pen_width, f_len, angle)
l_sys.add_rules(("X", "-YF+XFX+FY-"), ("Y", "+XF-YFY-FX+"))
l_sys.generate_path(5)
l_sys.draw_turtle( (0, 0), 0)

Попробуйте самостоятельно разобраться как представленные аксиомы и правила формируют такие фрактальные кривые. А на следующем занятии мы продолжим погружаться в это направление и построим L-системы с возможностью ветвления кривых.

L-система для дракона Хартера-Хайтвея, ковра Серпинского и кривой Гильберта

Видео по теме