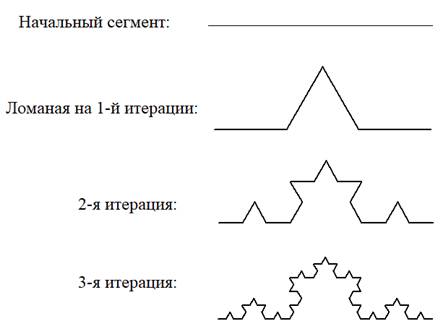
Кривая Коха и снежинка Коха

Я решил начать знакомство с фракталами с простого классического примера – кривой Коха. Строится она по простому правилу: каждый ее линейный сегмент на последующей итерации заменяется ломаной:

Начинать можно с прямой линии. Затем, на 1-й итерации она заменяется ломаной, состоящей из 4-х линейных сегментов равной длины. Причем, длина этой ломаной в точности равна длине линейного сегмента. То есть, углы между прямыми составляют 60 градусов. На 2-й итерации каждый линейный сегмент заменяется точно такой же ломаной, только уменьшенной в три раза. И так далее. В результате, у нас получается самоподобная кривая, которая получила название кривой Коха в честь автора – шведского математика Хельге фон Коха:

(1870-1924 гг.)

В то время еще не было понятия фракталов и это был лишь пример кривой, которая всюду непрерывна, но нигде не дифференцируема. Математик Шарль Эрмит окрестил их «монстрами», а общее научное мнение полагало, что это пример некой математической «патологии» интересной, скорее, исследователям, чем настоящим ученым. Знали бы они тогда, что именно такие кривые лягут в основу описания многих реальных природных процессов и форм. Новые революционные идеи часто в истории встречали такое неприятие.

Но вернемся к кривой Коха. Это пример фрактальной формы. По каким признакам сделан такой вывод? Во-первых, это самоподобие. Здесь отчетливо видно, что на большем масштабе кривая будет оставаться визуально неизменной. Но одного самоподобия мало. Например, известная картина «Черный квадрат» Малевича тоже обладает самоподобием. Этот квадрат можно составить из четырех квадратов меньшей размерности:

Однако, гений Малевича все же не создал фрактала. Что еще не хватает для получения фрактальной формы? Дробной размерности! Квадрат принадлежит плоскости, имеет целую размерность 2, а кривая Коха – находится в дробной размерности, примерно, 1,2618. Я пока опущу вопрос как она была вычислена, мы к этому еще вернемся, главное, что фракталы должны принадлежать дробной размерности. Получаем два важных условия, которыми обладают фрактальные формы:

1) должна быть самоподобной;

2) должна принадлежать дробной размерности.

Обратите внимание, это не определение фракталов. Сам термин (фрактал) все еще находится в развитии и пока полностью не определен. Но эти два условия, на мой взгляд, должны выполняться.

Итак, что же придает фракталам дробная размерность и почему она так важна? Давайте еще наз взглянем на кривую Коха.

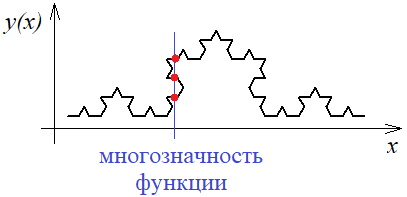
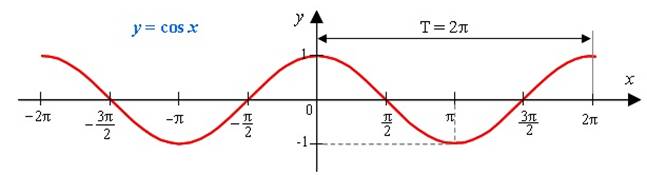
Если ее представить в координатных осях, то получим, что одному значению x соответствует несколько значений y. Такие кривые уже не являются одномерными, когда одному значению x соответствует только одно значение y, например, функция cos(x) одномерна:

И в то же время, множество точек кривой Коха по вертикали не выстраиваются в непрерывную линии, а значит, не покрывают все двумерное пространство. Отсюда и получается дробная размерность между единицей и двойкой. Благодаря этой дробности, множество точек кривой Коха образуют узор, а не просто заполняют двумерное пространство, как это было в случае «Черного квадрата» Малевича. Поэтому дробность размерности – характерная черта, наверное, всех фракталов.

Интересной особенностью кривой Коха является ее длина: она постоянно увеличивается по мере увеличения итераций. Действительно, вначале отрезок условно можно принять за 1. Затем, на 1-й итерации он заменяется ломаной, длина которой равна 4/3. На 2-й итерации каждый линейный сегмент заменяется уменьшенной ломаной длиной (4/3)/3 = 4/6 и таких сегментов ровно 4, то есть, суммарная длина линии, равна . 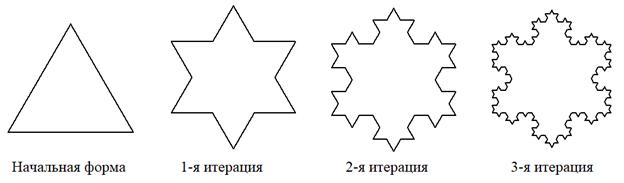На следующей итерации длина станет , и так далее. Получается, что при числе итераций, стремящихся к бесконечности, длина:

А что с площадью фрактальных фигур? Она тоже будет увеличиваться до бесконечности? Давайте посмотрим. Для этого сделаем построение уже не кривой Коха, а снежинки Коха. Здесь все делается аналогично, только начальная форма является равносторонним треугольником, а не линией:

Если начальную площадь равностороннего треугольника принять за единицу, то на первой итерации площадь увеличится на три малых треугольника, площади которых в раз меньше площади исходного треугольника. То есть, площадь составит:

На 2-й итерации имеем дополнительно 12 еще меньших треугольников с площадями в раз меньших, исходной площади:

И так далее, то есть, слагаемые в сумме стремительно уменьшаются при увеличении номера итерации и в пределе:

По-моему, неплохой способ предложить своим знакомым нарисовать фигуру с бесконечным периметром, но конечной площадью. У большинства задачка вызовет недоумение – как такое возможно? В школьной программе такого пока не проходят.

Итак, мы с вами познакомились с принципами формирования кривой Коха и снежинки Коха. Узнали о двух необходимых условиях, формирующих фрактальные формы: самоподобие и дробность размерности. И образно попытались уловить восприятие дробного пространства. Если эти моменты вам понятны, то цель этого занятия достигнута.

Кривая Коха и снежинка Коха

Видео по теме