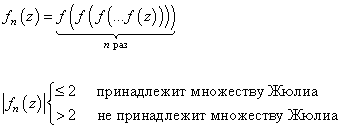|
Рисуем множество МандельбротаАрхив проекта: 14_fractals.py На прошлом занятии мы с вами построили несколько разных множеств Жюлиа, используя простую формулу:
где z, c – некие комплексные числа. На этом занятии мы будем строить множество Мандельброта по той же самой формуле. У вас может возникнуть вопрос, как используя одну и ту же формулу можно строить разные множества? Все дело в интерпретации. Я коротко напомню алгоритм для нахождения точек множеств Жюлиа.
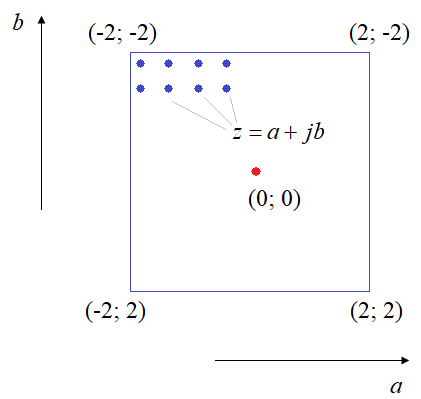
Мы сканировали множество точек на комплексной плоскости, например, в диапазоне [-2; 2] по мнимой и действительной осям и если в текущей точке функция
по рекурсии не уходила в бесконечность, не превышала порог 2, то делали вывод, что она относится к множеству Жюлиа:
Набор точек для
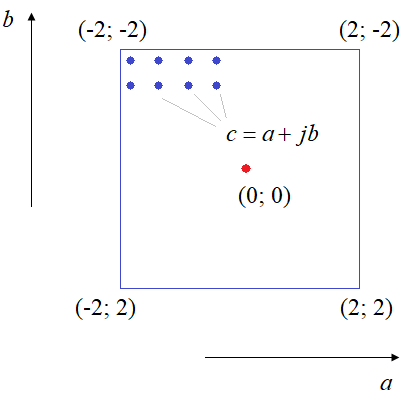
множества Мандельброта отбирается несколько иначе. Пробегпясь по комплексной
плоскости, мы формируем значение
После итерирования функции, мы также проверяем ее модуль (длину) на значение 2. Если он меньше, то точка принадлежит множеству Мандельброта. Иначе – не принадлежит. Программа предыдущего занятия для построения множества Мандельброта очень просто модифицируется. В заголовке окна напишем: pygame.display.set_caption("Множество Мандельброта") Установим начальные значения переменных для формирования изображения: P = 200 # размер [2*P+1 x 2*P+1] scale = P / 2 # масштабный коэффициент view = (0, 0) # координаты смещения угла обзора n_iter = 100 # число итераций для проверки принадлежности к множеству Мандельброта И, затем, в цикле сформируем переменную c и начальное значение z: c = complex(a, b) z = complex(0) И это все. Запускаем программу, видим результат:
Это и есть изображение множества Мандельброта на самом крупном масштабе. Если нарисовать его без раскраски, то увидим только черные точки множества и белые – вне его:
Но это не очень красиво, поэтому я верну краски в изображение. Давайте увеличим изображение и посмотрим на его более мелкие детали: scale = P / 0.5 # масштабный коэффициент view = (0, -200) # координаты смещения угла обзора Получится, следующее:
Если мы будем приближать фрагменты этого множества и рассматривать его на все более мелких масштабах, то этот процесс может быть бесконечным. У этого множества нет предела в мелких деталях. Оно самоподобно. С каждым новым масштабом практически повторяется снова и снова. И так до бесконечности. Каждый из вас теперь может создать программу для визуализации и масштабирования этого изображения и даже создать визуализацию, подобно той, что вы наблюдаете сейчас. Как видите, для этого достаточно всего одной маленькой формулы, чтобы получить такое богатство деталей фрактальных форм. Впервые, полученное изображение множества Мандельброта в 1980 году, впоследствии назвали отпечатком пальца Бога. Действительно, мы здесь видим удивительный акт творения, практически из ничего. Еще совсем недавно в исторической перспективе в подобное мало кто мог бы поверить. Но теперь, перед нами раскрылось все богатство фрактальных процессов и форм. Это, безусловно, раздвинуло горизонты нашего сознания, позволило лучше понять фундаментальные процессы природы и, возможно, самого акта рождения упорядоченных форм во вселенной. Видео по теме |